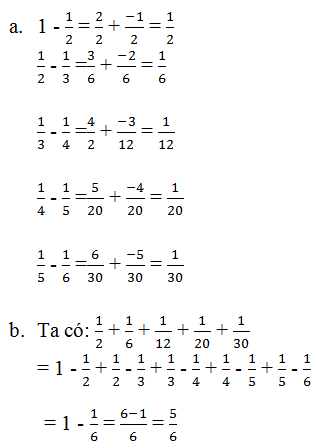tính Q =\(\dfrac{1}{2-\dfrac{1}{2-\dfrac{1}{2-\dfrac{1}{2}}}}\)

Những câu hỏi liên quan
Tính Q= \(\dfrac{1}{1+\left(\dfrac{1}{2021}\right)^2}+\dfrac{1}{1+\left(\dfrac{2}{2020}\right)^2}+...+\dfrac{1}{1+\left(\dfrac{2021}{1}\right)^2}\)
1,tính:
a,\(\dfrac{1}{1-\dfrac{1}{1-\dfrac{1}{2}}}+\dfrac{1}{1-\dfrac{1}{1-\dfrac{1}{2}}}\)
b,\(\dfrac{1}{1-\dfrac{1}{1-\dfrac{1}{3}}}+\dfrac{1}{1-\dfrac{1}{1-\dfrac{1}{3}}}\)
\(tính:\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{7}-\dfrac{1}{6}+\dfrac{1}{5}-\dfrac{1}{4}+\dfrac{1}{3}-\dfrac{1}{2}\)
\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{8}-\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{7}\)
\(\left(\dfrac{1}{2}-\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}+\dfrac{1}{3}\right)+\left(\dfrac{1}{4}-\dfrac{1}{4}\right)+\left(-\dfrac{1}{5}+\dfrac{1}{5}\right)+\left(\dfrac{1}{6}-\dfrac{1}{6}\right)+\left(\dfrac{-1}{7}+\dfrac{1}{7}\right)+\dfrac{1}{8}\)
=0+0+0+0+0+0+\(\dfrac{1}{8}\)
=\(\dfrac{1}{8}\)
Đúng 0
Bình luận (0)
a) Tính :
\(1-\dfrac{1}{2};\dfrac{1}{2}-\dfrac{1}{3};\dfrac{1}{3}-\dfrac{1}{4};\dfrac{1}{4}-\dfrac{1}{5};\dfrac{1}{5}-\dfrac{1}{6}\)
b) Sử dụng kết quả của câu a) để tính nhanh tổng sau :
\(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}\)
a) \(1-\dfrac{1}{2}=\dfrac{1}{2}\)
\(\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{3-2}{6}=\dfrac{1}{6}\)
\(\dfrac{1}{3}-\dfrac{1}{4}=\dfrac{4-3}{12}=\dfrac{1}{12}\)
\(\dfrac{1}{4}-\dfrac{1}{5}=\dfrac{5-4}{20}=\dfrac{1}{20}\)
\(\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{6-5}{30}=\dfrac{1}{30}\)
b) \(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}\)
\(=\left(1-\dfrac{1}{2}\right)+\left(\dfrac{1}{2}-\dfrac{1}{3}\right)+\left(\dfrac{1}{3}-\dfrac{1}{4}\right)+\left(\dfrac{1}{4}-\dfrac{1}{5}\right)+\left(\dfrac{1}{5}+\dfrac{1}{6}\right)\)
\(=1+\left(-\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}+\dfrac{1}{3}\right)+\left(-\dfrac{1}{4}+\dfrac{1}{4}\right)+\left(-\dfrac{1}{5}+\dfrac{1}{5}\right)+-\dfrac{1}{6}\)\(=1+-\dfrac{1}{6}\)
\(=\dfrac{5}{6}\)
Đúng 0
Bình luận (0)
Tính giá trị của các biểu thức sau1) A1+2+2^2+...+2^{2015}2) Bleft(dfrac{1}{4}-1right)cdotleft(dfrac{1}{9}-1right)cdotleft(dfrac{1}{16}-1right)cdotcdotcdotcdotcdotleft(dfrac{1}{400}-1right)3) Cleft(dfrac{1}{4cdot9}+dfrac{1}{9cdot14}+dfrac{1}{14cdot19}+...+dfrac{1}{44cdot49}right)cdotdfrac{1-3-5-7-...-49}{89}4) Ddfrac{2^{12}cdot3^5-4^6cdot9^2}{left(2^2cdot3right)^6+8^4cdot3^5}-dfrac{5^{10}cdot7^3-25^5cdot49^2}{left(125cdot7right)^3+5^9cdot14^3}5) Edfrac{dfrac{1}{2003}+dfrac{1}{2004}-dfrac{1}{2005...
Đọc tiếp
Tính giá trị của các biểu thức sau
1) \(A=1+2+2^2+...+2^{2015}\)
2) \(B=\left(\dfrac{1}{4}-1\right)\cdot\left(\dfrac{1}{9}-1\right)\cdot\left(\dfrac{1}{16}-1\right)\cdot\cdot\cdot\cdot\cdot\left(\dfrac{1}{400}-1\right)\)
3) \(C=\left(\dfrac{1}{4\cdot9}+\dfrac{1}{9\cdot14}+\dfrac{1}{14\cdot19}+...+\dfrac{1}{44\cdot49}\right)\cdot\dfrac{1-3-5-7-...-49}{89}\)
4) \(D=\dfrac{2^{12}\cdot3^5-4^6\cdot9^2}{\left(2^2\cdot3\right)^6+8^4\cdot3^5}-\dfrac{5^{10}\cdot7^3-25^5\cdot49^2}{\left(125\cdot7\right)^3+5^9\cdot14^3}\)
5) \(E=\dfrac{\dfrac{1}{2003}+\dfrac{1}{2004}-\dfrac{1}{2005}}{\dfrac{5}{2003}+\dfrac{5}{2004}-\dfrac{5}{2005}}-\dfrac{\dfrac{2}{2002}+\dfrac{2}{2003}-\dfrac{2}{2004}}{\dfrac{3}{2002}+\dfrac{3}{2003}-\dfrac{3}{2004}}\)
6) Cho 13+23+...+103=3025
Tính S= 23+43+63+...+203
tìm x,y viết dưới dạng phân số
a. 5+dfrac{x}{5+dfrac{2}{5+dfrac{3}{5+dfrac{4}{5}}}}dfrac{x}{1+dfrac{5}{2+dfrac{4}{3+dfrac{3}{5+dfrac{1}{6}}}}}
b.
dfrac{y}{3+dfrac{5}{2+dfrac{4}{2+dfrac{5}{2+dfrac{4}{2+dfrac{5}{3}}}}}}+dfrac{y}{7+dfrac{1}{3+dfrac{1}{3+dfrac{1}{4}}}}
2
c,
x.left(dfrac{1}{1+dfrac{1}{1+dfrac{1}{1+dfrac{1}{1+dfrac{1}{1+dfrac{1}{1+dfrac{1}{1+dfrac{1}{1+1}}}}}}}}right)2+dfrac{1}{2+dfrac{1}{2+dfrac{1}{2+dfrac{1}{2+dfrac{1}{2+dfrac{1}{2+dfrac{1}{2}}}}}}}+x.left(3+dfrac{1}{3-df...
Đọc tiếp
tìm x,y viết dưới dạng phân số
a. \(5+\dfrac{x}{5+\dfrac{2}{5+\dfrac{3}{5+\dfrac{4}{5}}}}=\dfrac{x}{1+\dfrac{5}{2+\dfrac{4}{3+\dfrac{3}{5+\dfrac{1}{6}}}}}\)
b.
\(\dfrac{y}{3+\dfrac{5}{2+\dfrac{4}{2+\dfrac{5}{2+\dfrac{4}{2+\dfrac{5}{3}}}}}}+\dfrac{y}{7+\dfrac{1}{3+\dfrac{1}{3+\dfrac{1}{4}}}}\)
= 2
c,
\(x.\left(\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+1}}}}}}}}\right)=\)\(2+\dfrac{1}{2+\dfrac{1}{2+\dfrac{1}{2+\dfrac{1}{2+\dfrac{1}{2+\dfrac{1}{2+\dfrac{1}{2}}}}}}}\)+\(x.\left(3+\dfrac{1}{3-\dfrac{1}{3+\dfrac{1}{3+\dfrac{1}{3-\dfrac{1}{3}}}}}\right)\)
Giair bằng máy tính casio
bài này đúng là thị của phi...vô của lí ... :))
Đúng 0
Bình luận (0)
Tính:
\(a,\dfrac{x+3}{2x-1}-\dfrac{x^2-5}{4x^2-4x+1}-\dfrac{2x^3+5x^2-x-1}{8x^3-12x^2+6x-1}\)
\(b,\dfrac{1}{1-x}+\dfrac{1}{1+x}+\dfrac{2}{1+x^2}+\dfrac{4}{1+x^4}+\dfrac{8}{1+x^8}+\dfrac{16}{1+x^{16}}\)
Trong các đẳng thức sau đây, đẳng thức minh họa tính chất kết hợp của phép nhân phân số đó là :
(A) dfrac{1}{3}.dfrac{1}{5}.dfrac{1}{2}dfrac{1}{3}.dfrac{1}{2}.dfrac{1}{5} (B) left(dfrac{1}{3}.dfrac{1}{5}right).dfrac{1}{2}dfrac{1}{3}.left(dfrac{1}{5}.dfrac{1}{2}right)
(C) dfrac{1}{3}.dfrac{1}{5}+dfrac{1}{3}.dfrac{1}{2}dfrac{1}{3}.left(dfrac{1}{5}+dfrac{1}{2}right) (D) dfrac{1}{3}.dfrac{1}{5}.dfrac{1}{2}left(dfrac{1}{3}.dfrac{1}{5}right).left(dfr...
Đọc tiếp
Trong các đẳng thức sau đây, đẳng thức minh họa tính chất kết hợp của phép nhân phân số đó là :
(A) \(\dfrac{1}{3}.\dfrac{1}{5}.\dfrac{1}{2}=\dfrac{1}{3}.\dfrac{1}{2}.\dfrac{1}{5}\) (B) \(\left(\dfrac{1}{3}.\dfrac{1}{5}\right).\dfrac{1}{2}=\dfrac{1}{3}.\left(\dfrac{1}{5}.\dfrac{1}{2}\right)\)
(C) \(\dfrac{1}{3}.\dfrac{1}{5}+\dfrac{1}{3}.\dfrac{1}{2}=\dfrac{1}{3}.\left(\dfrac{1}{5}+\dfrac{1}{2}\right)\) (D) \(\dfrac{1}{3}.\dfrac{1}{5}.\dfrac{1}{2}=\left(\dfrac{1}{3}.\dfrac{1}{5}\right).\left(\dfrac{1}{3}.\dfrac{1}{2}\right)\)
Hãy chọn đáp án đúng ?
Trong các đẳng thức trên ,đẳng thức minh họa tính chất kết hợp của phép nhân phân số đó là :
(B) \(\left(\dfrac{1}{3}.\dfrac{1}{5}\right).\dfrac{1}{2}=\dfrac{1}{3}\left(\dfrac{1}{5}.\dfrac{1}{2}\right)\)
Đúng 0
Bình luận (0)
BT1: CMR:
a) dfrac{1}{2^2}+dfrac{1}{3^2}+dfrac{1}{4^2}+...+dfrac{1}{n^2} 1
b) dfrac{1}{4}+dfrac{1}{16}+dfrac{1}{36}+dfrac{1}{64}+dfrac{1}{100}+dfrac{1}{144}+dfrac{1}{196} dfrac{1}{2}
c) dfrac{1}{3}+dfrac{1}{30}+dfrac{1}{32}+dfrac{1}{35}+dfrac{1}{45}+dfrac{1}{47}+dfrac{1}{50} dfrac{1}{2}
d) dfrac{1}{2}-dfrac{1}{4}+dfrac{1}{8}-dfrac{1}{16}+dfrac{1}{32}-dfrac{1}{64} dfrac{1}{3}
e) dfrac{1}{3} dfrac{2}{3^2}+dfrac{3}{3^3}-dfrac{4}{3^4}+...+dfrac{99}{3^{99}}-dfrac{100}{3^{100}} dfrac{3}{16}
f) d...
Đọc tiếp
BT1: CMR:
a) \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{n^2}< 1\)
b) \(\dfrac{1}{4}+\dfrac{1}{16}+\dfrac{1}{36}+\dfrac{1}{64}+\dfrac{1}{100}+\dfrac{1}{144}+\dfrac{1}{196}< \dfrac{1}{2}\)
c) \(\dfrac{1}{3}+\dfrac{1}{30}+\dfrac{1}{32}+\dfrac{1}{35}+\dfrac{1}{45}+\dfrac{1}{47}+\dfrac{1}{50}< \dfrac{1}{2}\)
d) \(\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{8}-\dfrac{1}{16}+\dfrac{1}{32}-\dfrac{1}{64}< \dfrac{1}{3}\)
e) \(\dfrac{1}{3}< \dfrac{2}{3^2}+\dfrac{3}{3^3}-\dfrac{4}{3^4}+...+\dfrac{99}{3^{99}}-\dfrac{100}{3^{100}}< \dfrac{3}{16}\)
f) \(\dfrac{1}{41}+\dfrac{1}{42}+\dfrac{1}{43}+...+\dfrac{1}{79}+\dfrac{1}{80}>\dfrac{7}{12}\)
BT2: Tính tổng
a) A=\(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{100}}\)
b) E=\(1+\dfrac{1}{2}\left(1+2\right)+\dfrac{1}{3}\left(1+2+3\right)+\dfrac{1}{4}\left(1+2+3+4\right)+...+\dfrac{1}{200}\left(1+2+3+...+200\right)\)
BT3: Cho S=\(\dfrac{3}{10}+\dfrac{3}{11}+\dfrac{3}{12}+\dfrac{3}{13}+\dfrac{3}{14}\)
CMR: 1 < S < 2
bài này có trong sách Nâng cao và Phát triển bạn nhé
Đúng 0
Bình luận (0)
Tính giá trị biểu thức :
1. Adfrac{dfrac{2}{5}+dfrac{2}{7}-dfrac{2}{9}-dfrac{2}{11}}{dfrac{4}{5}+dfrac{4}{7}-dfrac{4}{9}-dfrac{4}{11}}
2. Bdfrac{1^2}{1cdot2}cdotdfrac{2^2}{2cdot3}cdotdfrac{3^2}{3cdot4}cdotdfrac{4^2}{4cdot5}
3. Cdfrac{2^2}{1cdot3}cdotdfrac{3^2}{2cdot4}cdotdfrac{4^2}{3cdot5}cdotdfrac{5^2}{4cdot6}cdotdfrac{5^2}{4cdot6}
4. Dleft(dfrac{4}{5}-dfrac{1}{6}right)cdotleft(dfrac{2}{3}cdotdfrac{1}{4}right)^2
5. Cho M8dfrac{2}{7}-left(3dfrac{4}{9}+4dfrac{2}{7}right) ; Nleft(10dfrac{2}...
Đọc tiếp
Tính giá trị biểu thức :
1. \(A=\dfrac{\dfrac{2}{5}+\dfrac{2}{7}-\dfrac{2}{9}-\dfrac{2}{11}}{\dfrac{4}{5}+\dfrac{4}{7}-\dfrac{4}{9}-\dfrac{4}{11}}\)
2. \(B=\dfrac{1^2}{1\cdot2}\cdot\dfrac{2^2}{2\cdot3}\cdot\dfrac{3^2}{3\cdot4}\cdot\dfrac{4^2}{4\cdot5}\)
3. \(C=\dfrac{2^2}{1\cdot3}\cdot\dfrac{3^2}{2\cdot4}\cdot\dfrac{4^2}{3\cdot5}\cdot\dfrac{5^2}{4\cdot6}\cdot\dfrac{5^2}{4\cdot6}\)
4. \(D=\left(\dfrac{4}{5}-\dfrac{1}{6}\right)\cdot\left(\dfrac{2}{3}\cdot\dfrac{1}{4}\right)^2\)
5. Cho \(M=8\dfrac{2}{7}-\left(3\dfrac{4}{9}+4\dfrac{2}{7}\right)\) ; \(N=\left(10\dfrac{2}{9}+2\dfrac{3}{5}\right)-6\dfrac{2}{9}\). Tính \(P=M-N\)
6. \(E=10101\left(\dfrac{5}{111111}+\dfrac{5}{222222}-\dfrac{4}{3\cdot7\cdot11\cdot13\cdot37}\right)\)
7. \(F=\dfrac{\dfrac{1}{3}+\dfrac{1}{7}-\dfrac{1}{13}}{\dfrac{2}{3}+\dfrac{2}{7}-\dfrac{2}{13}}\cdot\dfrac{\dfrac{3}{4}-\dfrac{3}{16}-\dfrac{3}{256}+\dfrac{3}{64}}{1-\dfrac{1}{4}+\dfrac{1}{16}-\dfrac{1}{64}}+\dfrac{5}{8}\)
8. \(G=\text{[}\dfrac{\left(6-4\dfrac{1}{2}\right):0,03}{\left(3\dfrac{1}{20}-2,65\right)\cdot4+\dfrac{2}{5}}-\dfrac{\left(0,3-\dfrac{3}{20}\right)\cdot1\dfrac{1}{2}}{\left(1,88+2\dfrac{3}{25}\right)\cdot\dfrac{1}{80}}\text{]}:\dfrac{49}{60}\)
9. \(H=\dfrac{1}{1\cdot2\cdot3}+\dfrac{1}{2\cdot3\cdot4}+\dfrac{1}{4\cdot5\cdot6}+...+\dfrac{1}{98\cdot99\cdot100}\)
10. \(I=\dfrac{8}{9}\cdot\dfrac{15}{16}\cdot\dfrac{24}{25}\cdot...\cdot\dfrac{2499}{2500}\)
11. \(K=\left(-1\dfrac{1}{2}\right)\left(-1\dfrac{1}{3}\right)\left(-1\dfrac{1}{4}\right)...\left(-1\dfrac{1}{999}\right)\)
12. \(L=1\dfrac{1}{3}+1\dfrac{1}{8}+1\dfrac{1}{15}...\) (98 thừa số)
13. \(M=-2+\dfrac{1}{-2+\dfrac{1}{-2+\dfrac{1}{-2+\dfrac{1}{3}}}}\)
14. \(N=\dfrac{155-\dfrac{10}{7}-\dfrac{5}{11}+\dfrac{5}{23}}{403-\dfrac{26}{7}-\dfrac{13}{11}+\dfrac{13}{23}}\)
15. \(P=\left(\dfrac{1}{4}-1\right)\left(\dfrac{1}{5}-1\right)...\left(\dfrac{1}{2001}-1\right)\)
16. \(Q=\left(\dfrac{1}{1\cdot2}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+...+\dfrac{1}{2005\cdot2006}\right):\left(\dfrac{1}{1004\cdot2006}+\dfrac{1}{1005\cdot2005}+...+\dfrac{1}{2006\cdot1004}\right)\)
1. \(A=\dfrac{2\left(\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{9}-\dfrac{1}{11}\right)}{4\left(\dfrac{1}{5}+\dfrac{1}{7}-\dfrac{1}{9}-\dfrac{1}{11}\right)}=\dfrac{2}{4}=\dfrac{1}{2}\)
2. \(B=\dfrac{1^2.2^2.3^2.4^2}{1.2^2.3^2.4^2.5}=\dfrac{1}{5}\)
3.\(C=\dfrac{2^2.3^2.\text{4^2.5^2}.5^2}{1.2^2.3^2.4^2.5.6^2}=\dfrac{125}{36}\)
4.D=\(D=\left(\dfrac{4}{5}-\dfrac{1}{6}\right).\dfrac{4}{9}.\dfrac{1}{16}=\dfrac{19}{30}.\dfrac{1}{36}=\dfrac{19}{1080}\)
Đúng 0
Bình luận (0)