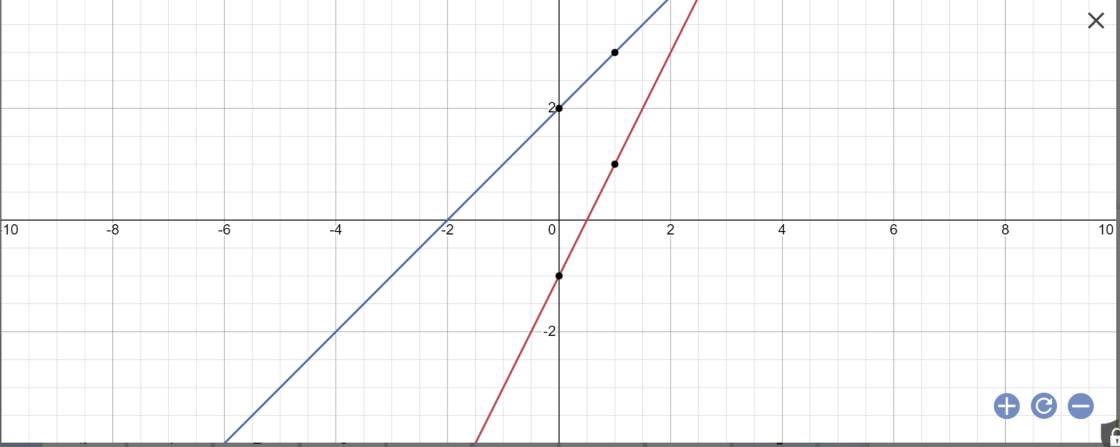
Bài 1*: Cho đường thẳng \(\Delta:y=-2x+1\) và điểm \(M\left(-1;-3\right)\) trên hệ trục tọa độ \(Oxy\). Hãy tính khoảng cách từ:
a) Từ \(O\) đến \(\Delta\)
b) Từ \(M\) đến \(\Delta\)
Bài 2: Ba đường thẳng sau đây có đồng quy hay không?
\(d_1:y=x-m+1,d_2:y=2x\) và \(d_3:y=2\left(2m-1\right)x+\dfrac{1}{4}\)