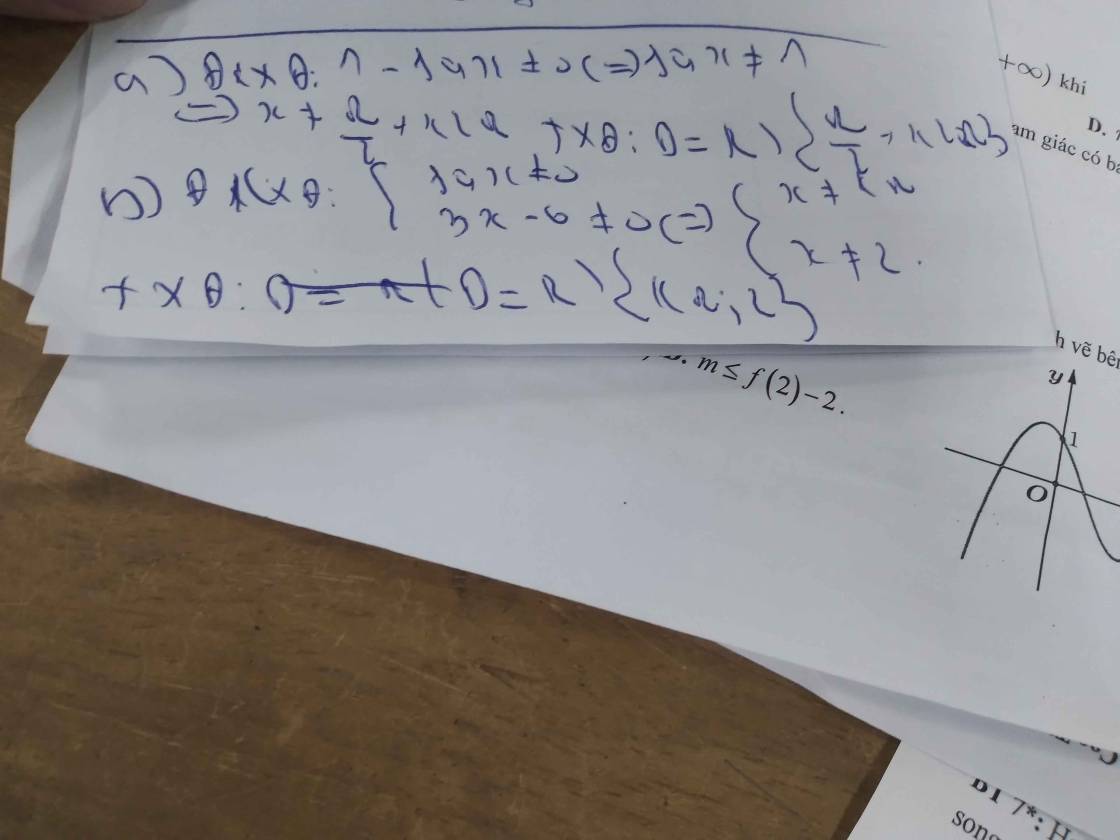\(y=\sqrt{\dfrac{sinx+2}{1-sinx}}\) tìm điều kiện xác định

Những câu hỏi liên quan
a) y = \(\dfrac{sinx}{2sinx+1}\)
b) y = \(\dfrac{sinx}{\sqrt{1-sinx}}\)
Tìm tập xác định có biến
a: ĐKXĐ: 2sin x+1<>0
=>sin x<>-1/2
=>x<>-pi/6+k2pi và x<>7/6pi+k2pi
b: ĐKXĐ: 1-sin x>0
=>sin x<1
=>x<>pi/2+k2pi
Đúng 1
Bình luận (0)
tìm tập xác định của hàm số
a. y=\(\dfrac{sinx}{cosx-1}\)
b.y=\(\sqrt{sinx-1}\)
c.y=\(\sqrt{\dfrac{1+sinx}{1-cosx}}\)
a: ĐKXĐ: \(cosx-1\ne0\)
=>\(cosx\ne1\)
=>\(x\ne k2\Omega\)
b: ĐKXĐ: sin x-1>=0
=>sin x>=1
mà \(-1< =sinx< =1\)
nên sin x=1
=>\(x=\dfrac{\Omega}{2}+k2\Omega\)
c:
-1<=sin x<=1
=>-1+1<=sin x+1<=1+1
=>0<=sin x+1<=2
ĐKXĐ: \(\dfrac{1+sinx}{1-cosx}>=0\)
mà \(1+sinx>=0\)(cmt)
nên \(1-cosx>0\)
=>\(cosx< 1\)
mà -1<=cosx<=1
nên \(cosx\ne1\)
=>\(x\ne k2\Omega\)
Đúng 0
Bình luận (0)
Tìm tập xác định của hàm số
1/ \(y=\dfrac{sinx}{\sqrt{3-cosx}}\)
2/ \(y=\sqrt{1-sin3x}\)
3/ \(y=\dfrac{tan2x+1}{sinx}\)
4/ \(y=sin\sqrt{2x-1}\)
1: ĐKXĐ: 3-cosx>0
=>cosx<3(luôn đúng)
2: ĐKXĐ: 1-sin 3x>=0
=>sin 3x<=1(luôn đúng)
3: ĐKXĐ: sin x<>0 và 2x<>pi/2+kpi
=>x<>kpi và x<>pi/4+kpi/2
4: ĐKXĐ: 2x-1>=0
=>x>=1/2
Đúng 1
Bình luận (0)
Tìm tập xác định của các hàm số sau:1,ysindfrac{3x+2}{2x-1}2,ytanleft(3x+dfrac{2pi}{5}right)3,ycotleft(2x-dfrac{1}{3}right)4,ydfrac{sinx+cosx}{sinx-cosx}5,ydfrac{1}{sinx}+dfrac{1}{cosx}6,ydfrac{sqrt{1-sinx}}{cosx}7,ydfrac{3}{sin^2x-cos^2x}8,ydfrac{1+tanx}{1+sinx}9,ysqrt{dfrac{1+sinx}{1-cosx}}
Đọc tiếp
Tìm tập xác định của các hàm số sau:
1,\(y=sin\dfrac{3x+2}{2x-1}\)
2,\(y=tan\left(3x+\dfrac{2\pi}{5}\right)\)
3,\(y=cot\left(2x-\dfrac{1}{3}\right)\)
4,\(y=\dfrac{sinx+cosx}{sinx-cosx}\)
5,\(y=\dfrac{1}{sinx}+\dfrac{1}{cosx}\)
6,\(y=\dfrac{\sqrt{1-sinx}}{cosx}\)
7,\(y=\dfrac{3}{sin^2x-cos^2x}\)
8,\(y=\dfrac{1+tanx}{1+sinx}\)
9,\(y=\sqrt{\dfrac{1+sinx}{1-cosx}}\)
tìm tập xác định của hàm số
1.y=\(cot\left(\dfrac{\pi}{3}-x\right)\)
2.y=\(\dfrac{tan2x-1}{\sqrt{1+sinx}+1}\)
3.y=\(\sqrt{\sqrt{1+sinx}-\sqrt{2}}\)
4.y=\(\dfrac{3cos4x-3}{\sqrt{2-2cosx}-2}\)
5.y=\(\dfrac{1-cot3x}{1-\sqrt{1+sin3x}}\)
6.y=\(cot2x+cotx\)
1. \(sin\left(\dfrac{\pi}{3}-x\right)\ne0\Leftrightarrow\dfrac{\pi}{3}-x\ne k\pi\Leftrightarrow x\ne\dfrac{\pi}{3}-k\pi\)
2. \(cos2x\ne0\Leftrightarrow2x\ne\dfrac{\pi}{2}+k\pi\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)
3. \(\sqrt{1+sinx}-\sqrt{2}\ge0\Leftrightarrow1+sinx\ge2\Leftrightarrow sinx\ge1\Leftrightarrow sinx=1\Leftrightarrow x=\dfrac{\pi}{2}+k2\pi\)
4. \(\sqrt{2-2cosx}-2\ne0\Leftrightarrow2-2cosx\ne4\Leftrightarrow cosx\ne-1\Leftrightarrow x\ne\pi+k2\pi\)
5. \(1-\sqrt{1+sin3x}\ne0\Leftrightarrow sin3x\ne0\Leftrightarrow3x\ne k\pi\Leftrightarrow x\ne\dfrac{k\pi}{3}\)
Đúng 1
Bình luận (2)
Tìm tập xác định của hàm số sau
a) y=cot(\(3x+\dfrac{\pi}{6}\)) + \(\dfrac{tan2x}{sinx+1}\)
b) y=\(\sqrt{5+2cot^2x-sinx}\) + cot\(\left(\dfrac{\pi}{2}+x\right)\)
a.
\(\left\{{}\begin{matrix}sin\left(3x+\dfrac{\pi}{6}\right)\ne0\\cos2x\ne0\\sinx\ne-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne-\dfrac{\pi}{18}+\dfrac{k\pi}{3}\\x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x\ne-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
b.
Do \(5+2cot^2x-sinx=4+2cot^2x+\left(1-sinx\right)>0\) nên hàm xác định khi:
\(\left\{{}\begin{matrix}sinx\ne0\\sin\left(x+\dfrac{\pi}{2}\right)\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow sin2x\ne0\)
\(\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
Đúng 2
Bình luận (0)
tìm tập xác định
\(y=\sqrt{\dfrac{1+cosx}{1-sinx}}\)
ĐKXĐ: \(\left\{{}\begin{matrix}\dfrac{1+cosx}{1-sinx}\ge0\left(luôn-đúng\right)\\1-sinx\ne0\end{matrix}\right.\)
\(\Rightarrow sinx\ne1\)
\(\Rightarrow x\ne\dfrac{\pi}{2}+k2\pi\)
Đúng 3
Bình luận (4)
tìm tập xác định của hàm số
a) y = \(\dfrac{2}{1-sinx}\)
b) y = \(\dfrac{5-x}{sinx}\) - \(\dfrac{1}{3x-6}\)
tìm tập xác định của hàm số
y=\(\sqrt{\dfrac{1+sinx}{1-cosx}}\)
Ta có:
`@-1 <= sin x <= 1`
`<=>0 <= 1+sin x <= 2=>1+sin x >= 0`
`@-1 <= cos x <= 1`
`<=>1 >= -cos x >= -1`
`<=>2 >= 1-cos x >= 0=>1-cos x >= 0`
Hàm số xác định `<=>[1+sin x]/[1-cos x] >= 0`
`<=>{(1+sin x >= 0(L Đ)),(1-cos x > 0):}<=>1-cos x ne 0<=>x ne k2\pi (k in ZZ)`
`=>TXĐ: D=R\\{k2\pi| k in ZZ}`.
Đúng 0
Bình luận (0)
1, Tìm txd của hàm số sau
a, y = \(\sqrt{sinx-1}\)
b, y =\(\sqrt{\dfrac{1-sinx}{1+sinx}}\)
c, y = \(\dfrac{1+cosx}{sinx}\)
ĐKXĐ: (tất cả \(k\in Z\))
a. \(sinx-1\ge0\Leftrightarrow sinx\ge1\)
\(\Leftrightarrow sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b. \(\left\{{}\begin{matrix}\dfrac{1-sinx}{1+sinx}\ge0\left(luôn-đúng\right)\\1+sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow sinx\ne-1\)
\(\Leftrightarrow x\ne-\dfrac{\pi}{2}+k2\pi\)
c. \(sinx\ne0\Leftrightarrow x\ne k\pi\)
Đúng 1
Bình luận (0)