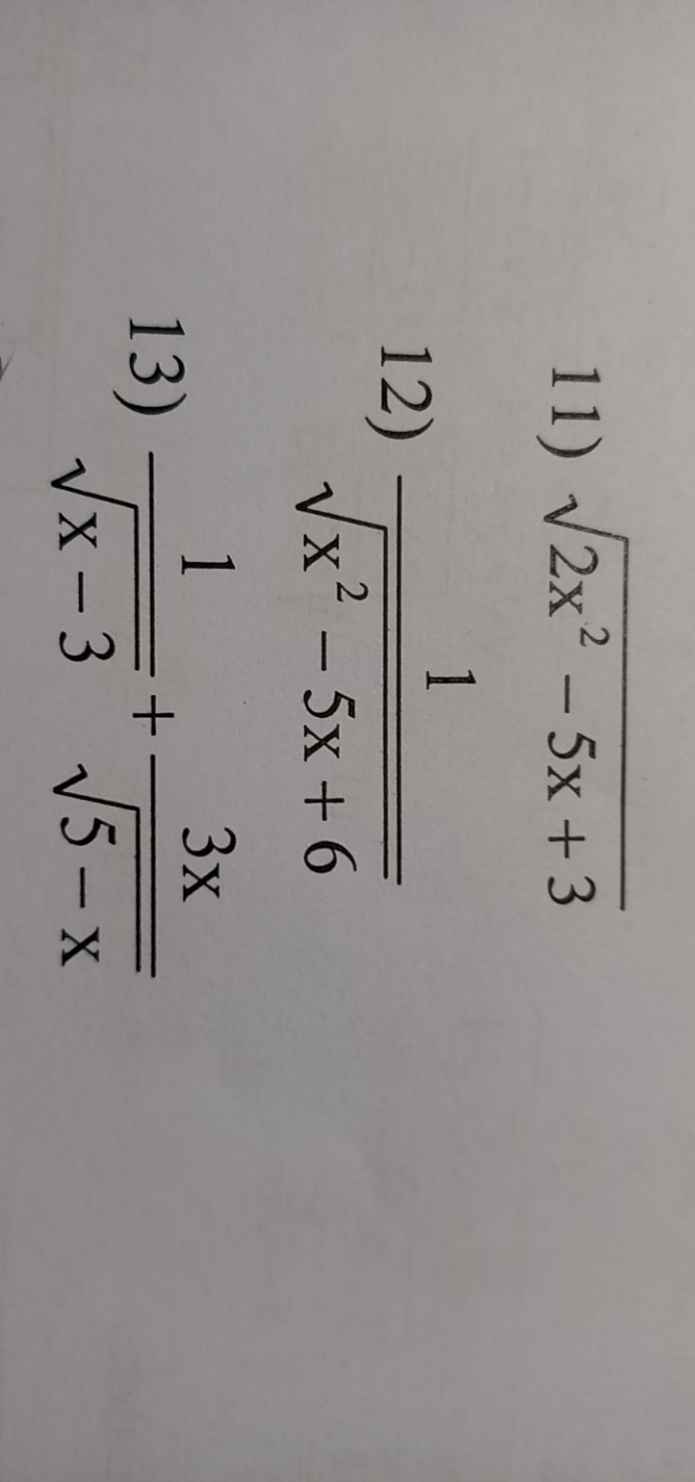
Giúp em ba câu này đề bài là tìm x để biểu thức sau có nghĩa (đkxđ của các biểu thức sau)
giúp mình bài này vs ạ
bài 1:so sánh các căn sau
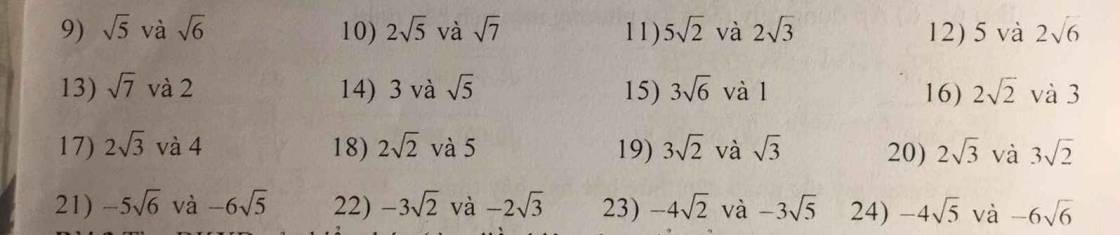
bài 2 :tìm ĐKXĐ của biểu thức (tìm đk của x để biểu thức sau có nghĩa)
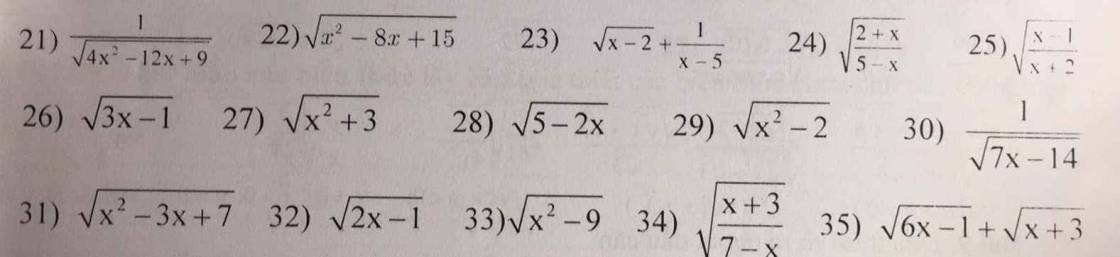
Bài 1
Mình làm mẫu một số câu thôi nhé
\(9,\sqrt{5}=\left(\sqrt{5}\right)^2=5\\ \sqrt{6}=\left(\sqrt{6}\right)^2=6\)
Vì \(5< 6\)
\(\Rightarrow\sqrt{5}< \sqrt{6}\)
\(10,2\sqrt{5}=\left(2\sqrt{5}\right)^2=20\\ \sqrt{7}=\left(\sqrt{7}\right)^2=7\)
Vì \(20>7\)
\(\Rightarrow2\sqrt{5}>\sqrt{7}\)
\(11,5\sqrt{2}=\left(5\sqrt{2}\right)^2=50\\ 2\sqrt{3}=\left(2\sqrt{3}\right)^2=12\)
Vì \(50>12\Rightarrow5\sqrt{2}>2\sqrt{3}\)
\(12,2\sqrt{6}=\left(2\sqrt{6}\right)^2=24\\ 5=5^2=25\)
Vì \(25>24\Rightarrow5>2\sqrt{6}\)
\(13,\sqrt{7}=\left(\sqrt{7}\right)^2=7\\ 2=2^2=4\)
Vì \(7>4\Rightarrow\sqrt{7}>2\)
\(14,3=3^2=9\\ \sqrt{5}=\left(\sqrt{5}\right)^2=5\)
Vì \(9>5\Rightarrow3>\sqrt{5}\)
\(15,3\sqrt{6}=\left(3\sqrt{6}\right)^2=54\)
Vì \(54>1\Rightarrow3\sqrt{6}>1\)
\(16,2\sqrt{2}=\left(2\sqrt{2}\right)^2=8\\ 3=3^2=9\)
Vì \(8< 9\Rightarrow2\sqrt{2}< 3\)
Phương pháp làm dạng bài này là bình phương hai vế rồi so sánh
Bài 2
Gợi ý : Biểu thức dưới dấu căn \(\ge\) 0
Lưu ý : Nếu biểu thức dưới dấu căn ở dưới mẫu thì \(>0\)
\(21,ĐK:4x^2-12x+9>0\\ \Rightarrow\left(2x-3\right)^2>0\\ \Leftrightarrow x\ne\dfrac{3}{2}\)
\(22,ĐK:x^2-8x+15\ge0\\ \Rightarrow\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\)
\(23,ĐK:\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)
\(24,ĐK:\left\{{}\begin{matrix}\dfrac{2+x}{5-x}\ge0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2+x\ge0\\5-x\ge0\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x\le5\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x< 5\end{matrix}\right.\left(t/m\right)\)
Hoặc
\(\left\{{}\begin{matrix}2+x\le0\\5-x\le0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\le-2\\x\ge5\\x\ne5\end{matrix}\right.\left(loại\right)\)
Chỉ đăng tối đa 10 - 15 câu hỏi thôi, câu trước GV nhắc bạn rồi mà giờ bạn vẫn còn đăng nữa thì nên bị xóa câu hỏi.
B. Bài tập cơ bản.
Bài 2.1
Tìm x để mỗi căn thức sau đây có nghĩa:
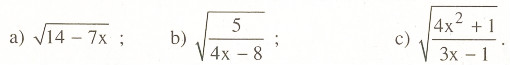
Bài 2.2
Tìm điều kiện của x để biểu thức sau đây có nghĩa:
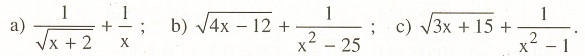
Bài 2.3
Tính:
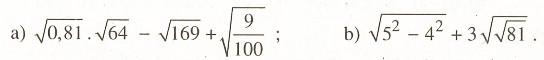
Bài 2.4
Rút gọn các biểu thức sau:
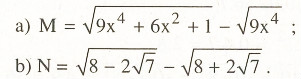
Bài 2.5
Giải các phương trình sau:
![]()
a) Căn thức có nghĩa `<=> 14-7x >=0 <=> x <= 2`
b) Căn thức có nghĩa `<=> 4x-8>0 <=> x>2`
`(5>=0 forall x)`
c) Căn thức có nghĩa `<=>3x-1 > 0 <=> x >1/3`
`(4x^2+1>0 forall x)`
a) Để \(\sqrt{14-7x}\) có nghĩa là 14 -7x ≥ 0
Ta có: 14 -7x ≥ 0
-7x ≥ -14
x ≤ 2
Vậy x ≤ 2
Tìm x để biểu thức sau có nghĩa. Mình yếu phần này lắm nên mong các bạn giúp mình. Cảm ơn nhìuuuu lắm
\(a,ĐKXĐ:\left\{{}\begin{matrix}8-4x\ge0\\5x-10\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le2\\x\ne2\end{matrix}\right.\Leftrightarrow x< 2\\ b,ĐKXĐ:\left\{{}\begin{matrix}\dfrac{-3}{x+2}\ge0\\x^2+2\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+2< 0\left(-3< 0;x+2\ne0\right)\\x\in R\left(x^2+2\ge2>0\right)\end{matrix}\right.\Leftrightarrow x< -2\)
Giúp mk với Bài 7: Xác định giá trị của biểu thức để các biểu thức sau có nghĩa: a) 5/(x - 2) b) (x - y)/(2x + 1) (x - 1)/(x ^ 2 + 1) d) (ax + by + c)/(xy - 3y)
a
Để biểu thức có nghĩa thì \(x-2\ne0\Rightarrow x\ne2\)
b
Để biểu thức có nghĩa thì \(2x+1\ne0\Rightarrow x\ne-\dfrac{1}{2}\)
c
Ủa câu c là (x-1)/(x^2+1) đúng không bạn:v
Để biểu thức có nghĩa thì \(x^2+1\ne0\)
Vì \(x^2\ge0\forall x\Rightarrow x^2+1>0\forall x\)
Vậy biểu thức có nghĩa với mọi giá trị x.
d
Để biểu thức có nghĩa thì \(xy-3y\ne0\Leftrightarrow y\left(x-3\right)\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}y\ne0\\x-3\ne0\Rightarrow x\ne3\end{matrix}\right.\)
Vậy để biểu thức có nghĩa thì đồng thời \(y\ne0,x\ne3\)
a) \(\dfrac{5}{x-2}\)
Có nghĩa khi:
\(x-2\ne0\)
\(\Rightarrow x\ne2\)
b) \(\dfrac{x-y}{2x+1}\)
Có nghĩa khi:
\(2x+1\ne0\)
\(\Rightarrow2x\ne-1\)
\(\Rightarrow x\ne-\dfrac{1}{2}\)
c) \(\dfrac{x-1}{x^2+1}\)
Có nghĩa khi:
\(x^2+1\ne0\)
\(\Rightarrow x^2\ne-1\) (luôn đúng)
Vậy biểu thức được xác định với mọi x
d) \(\dfrac{ax+by+c}{xy-3y}=\dfrac{ax+by+c}{y\left(x-3\right)}\)
Có nghĩa khi:
\(y\left(x-3\right)\ne0\)
\(\Leftrightarrow\left[{}\begin{matrix}y\ne0\\x-3\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}y\ne0\\x\ne3\end{matrix}\right.\)
giúp tôi giải câu này với :
a, tìm x=? để biểu thức sau có nghĩa A=1/x-1 +căn -2x+3
b, rút gọn biểu thức B=căn75 + căn 48 -1/2căn 300
c,giải phương trình : 4căn2 x^2 -6x-căn2=0
Bài 1 (2,0 điểm).
1. Thực hiện phép tính.
2. Tìm điều kiện của x để các biểu thức sau có nghĩa:
Bài 2 (2,0 điểm).
1. Phân tích đa thức thành nhân tử.
2. Giải phương trình:
Bài 3 (2,0 điểm. Cho biểu thức:
(với x > 0; x ≠ 1)
a. Rút gọn biểu thức A.
b. Tìm x để
Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
a. Tính độ dài các đoạn thẳng AB, AC, AH.
b. Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.
c. Chứng minh rằng:
Bài 5 (0,5 điểm).
Cho biểu thức P = x3 + y3 - 3(x + y) + 1993. Tính giá trị biểu thức P với:
Giúp vs ạ 1h nộp cô r
Bài 5:
\(x^3=18+3\sqrt[3]{\left(9+4\sqrt{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\\ \Leftrightarrow x^3=18+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=18\\ y^3=6+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow y^3=6+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=6\\ P=x^3+y^3-3\left(x+y\right)+1993\\ P=\left(x^3-3x\right)+\left(y^3-3y\right)+1993\\ P=18+6+1993=2017\)
x3=18+33√(9+4√5)(9−4√5)(3√9+4√5+3√9−4√5)⇔x3=18+3x3√1⇔x3−3x=18y3=6+33√(3−2√2)(3+2√2)(3√3+2√2+3√3−2√2)⇔y3=6+3y3√1⇔y3−3y=6P=x3+y3−3(x+y)+1993P=(x3−3x)+(y3−3y)+1993P=18+6+1993=2017
Bài 1: Giải phương trình sau:
\(2x^2+5+2\sqrt{x^2+x-2}=5\sqrt{x-1}+5\sqrt{x+2}\)
Bài 2: Cho biểu thức
\(P=\left(\frac{6x+4}{3\sqrt{3x^2}-8}-\frac{\sqrt{3x}}{3x+2\sqrt{3x}+4}\right).\left(\frac{1+3\sqrt{3x^2}}{1+\sqrt{3x}}-\sqrt{3x}\right)\)
a) Tìm ĐKXĐ và rút gọn biểu thức P
b) Tìm tất cả các giá trị nguyên của x để biểu thức P có giá trị nguyên
Bài 3: Cho biểu thức
\(A=\frac{\sqrt{x+4\sqrt{x-4}}+\sqrt{x-4\sqrt{x-4}}}{\sqrt{1-\frac{8}{x}+\frac{16}{x^2}}}\)
a) Tìm ĐKXĐ và rút gọn biểu thức A
b) Tìm tất cả các giá trị nguyên của x để biểu thức A có giá trị nguyên
Bài 1: Rút gọn biểu thức D = \(\sqrt{16x^4}-2x^2+1\)
Bài 2: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng điều kiện xác định”
e) E = \(\dfrac{2\sqrt{x}}{\sqrt{x}+3}\) ĐKXĐ: \(x\ge0\)
Bài 3: Tìm giá trị lớn nhất – nhỏ nhất của biểu thức sau : “ Dùng hằng đẳng thức ”
B = \(1-\sqrt{x^2-2x+2}\)
Bài 4: Cho P = \(\dfrac{4\sqrt{x}+10}{2\sqrt{x}-1}\left(x\ge0;x\ne\dfrac{1}{4}\right)\). Tính tổng các giá trị x nguyên để biểu thức P có giá trị nguyên
Bài 1:
Ta có: \(D=\sqrt{16x^4}-2x^2+1\)
\(=4x^2-2x^2+1\)
\(=2x^2+1\)
Tìm x để các biểu thức sau có nghĩa và rút gọn các biểu thức sau: a) x-√x /√x-1 - x-1/√x+1
\(\dfrac{x-\sqrt{x}}{\sqrt{x}-1}-\dfrac{x-1}{\sqrt{x}+1}\);\(ĐK:x\ge0;x\ne1\)
\(\Leftrightarrow\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(\Leftrightarrow\sqrt{x}-\left(\sqrt{x}-1\right)\)
\(\Leftrightarrow\sqrt{x}-\sqrt{x}+1\)
\(\Leftrightarrow1\)
a: \(=\sqrt{x}\cdot\dfrac{\left(\sqrt{x}-1\right)}{\sqrt{x}-1}-\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(=\sqrt{x}-\sqrt{x}+1=1\)
Câu 1: Tìm x để biểu thức sau có nghĩa:
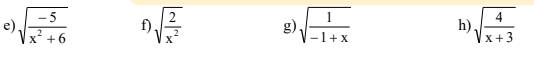
`e)` Biểu thức xác định `<=>[-5]/[x^2+6] >= 0`
`=>x^2+6 <= 0`
Mà `x^2+6 > 0`
`=>` Không có giá trị của `x` thỏa mãn.
`f)` Biểu thức xác định `<=>2/[x^2] >= 0`
`=>x^2 > 0<=>x ne 0`
`g)` Biểu thức xác định `<=>1/[-1+x] >= 0`
`=>-1+x > 0<=>x > 1`
`h)` Biểu thức xác định `<=>4/[x+3] >= 0`
`=>x+3 > 0<=>x > -3`
e) \(\sqrt{\dfrac{-5}{x^2+6}}\left(\text{k tồn tại x để biểu thức có ngĩa}\right)\left(\dfrac{-5}{x^2+6}< 0\forall x\right)\)
f) \(x\ne0\)
g) \(x>1\)
h) \(x>-3\)