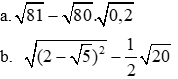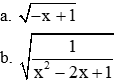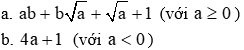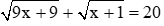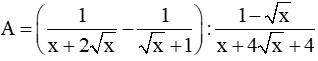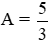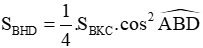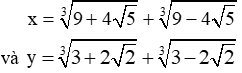Bài 1 (2,0 điểm).
1. Thực hiện phép tính.
2. Tìm điều kiện của x để các biểu thức sau có nghĩa:
Bài 2 (2,0 điểm).
1. Phân tích đa thức thành nhân tử.
2. Giải phương trình:
Bài 3 (2,0 điểm. Cho biểu thức:
(với x > 0; x ≠ 1)
a. Rút gọn biểu thức A.
b. Tìm x để
Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
a. Tính độ dài các đoạn thẳng AB, AC, AH.
b. Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.
c. Chứng minh rằng:
Bài 5 (0,5 điểm).
Cho biểu thức P = x3 + y3 - 3(x + y) + 1993. Tính giá trị biểu thức P với:
Giúp vs ạ 1h nộp cô r
Bài 5:
\(x^3=18+3\sqrt[3]{\left(9+4\sqrt{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\\ \Leftrightarrow x^3=18+3x\sqrt[3]{1}\\ \Leftrightarrow x^3-3x=18\\ y^3=6+3\sqrt[3]{\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\\ \Leftrightarrow y^3=6+3y\sqrt[3]{1}\\ \Leftrightarrow y^3-3y=6\\ P=x^3+y^3-3\left(x+y\right)+1993\\ P=\left(x^3-3x\right)+\left(y^3-3y\right)+1993\\ P=18+6+1993=2017\)
x3=18+33√(9+4√5)(9−4√5)(3√9+4√5+3√9−4√5)⇔x3=18+3x3√1⇔x3−3x=18y3=6+33√(3−2√2)(3+2√2)(3√3+2√2+3√3−2√2)⇔y3=6+3y3√1⇔y3−3y=6P=x3+y3−3(x+y)+1993P=(x3−3x)+(y3−3y)+1993P=18+6+1993=2017