Cho hàm số \(y=\dfrac{x-2}{x+1}\) và điểm I(-1;1) . Tìm các tiếp tuyến của đồ thị hàm số biết khoảng cách từ điểm I đến tiếp tuyến đó đạt giá trị lớn nhất

Những câu hỏi liên quan
Cho hàm số \(y=\dfrac{3x-1}{x-1}\) và điểm I(1;3) Tìm các tiếp tuyến của đồ thị hàm số biết tiếp tuyến đó cắt 2 đường thẳng x=1 và y=3 tạo thành 2 điểm A,B sao cho tam giác IAB cân tại I
cho hàm số: \(y=\left(2m-1\right)x+n\) với \(\left(m\ne\dfrac{1}{2}\right)\)
Tìm giá trị của m, n biết n=2m và đồ thị hàm số \(y=\left(2m-1\right)x+n\) cắt đồ thị hàm số \(y=\dfrac{1}{2}x-4\) tại một điểm trên trục tung
Vì hai đồ thị cắt nhau tại một điểm trên trục tung nên n=-4
=>m=-2
Đúng 0
Bình luận (0)
cho hàm số y = -x và y = \(-\dfrac{1}{2}\)x
a) vẽ trên cùng một hệ trục tọa độ oxy đồ thị của 2 hàm số trên
b) qua điểm H (0;-5) vẽ đường thẳng d song song với trục Ox cắt đường thẳng y = -x và y = \(-\dfrac{1}{2}\)x lần lượt ở A và B tìm tọa độ của các điểm A, B
c) tính chu vi và dienj tích tam giác OAB
a) 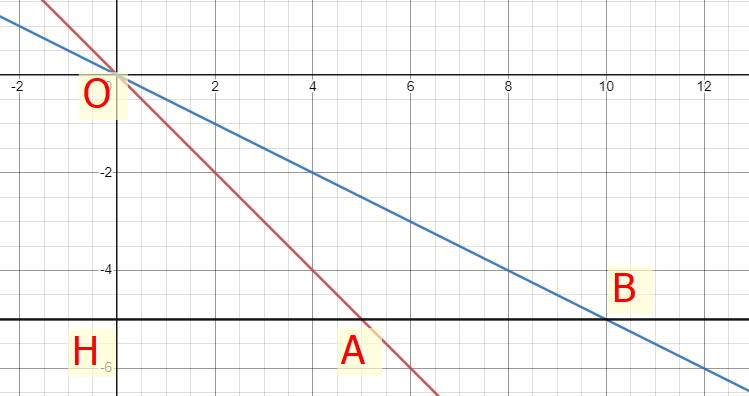
b) Ta có đường thẳng đi qua điểm H(0;-5) nên phương trình đường thẳng đi qua H là:
\(y=0x-5\Rightarrow y=-5\)
Phương trình hoành độ giao điểm của đường thẳng \(y=-5\) và \(y=-x\) là:
\(-5=-x\)
\(\Rightarrow x=5\)
Tọa độ điểm A là (5;-5)
Phương trình hoành độ giao điểm của đường thẳng \(y=-5\) và \(y=-\dfrac{1}{2}x\) là:
\(-5=-\dfrac{1}{2}x\)
\(\Rightarrow\dfrac{1}{2}x=5\)
\(\Rightarrow x=5:\dfrac{1}{2}\)
\(\Rightarrow x=10\)
Tọa độ điểm B là (10;-5)
c) Ta có: A(5;-5) và B(10;-5)
Độ dài đường thẳng AB là \(10-5=5\left(đvđd\right)\)
Có A(5;-5) ⇒ HA = 5 (đvđd)
Xét tam giác OHA vuông tại H áp dụng định lý Py-ta-go ta có:
\(OA^2=HA^2+OH^2\) (tọa độ điểm H(0;-5) nên OH = 5 đvđd)
\(\Rightarrow OA=\sqrt{5^2+5^2}=\sqrt{50}=5\sqrt{2}\left(đvđd\right)\)
Có B(10;-5) ⇒ HB = 10 (đvđd)
Xét tam giác OHB vuông tại H áp dụng định lý Py-ta-go ta có:
\(OB^2=HB^2+OH^2\)
\(\Rightarrow OB=\sqrt{10^2+5^2}=\sqrt{125}=5\sqrt{5}\left(đvđd\right)\)
Chu vi: \(C_{OAB}=AB+OA+OB=5+5\sqrt{2}+5\sqrt{5}\approx23,25\left(đvđd\right)\)
Diện tích: \(S_{OAB}=\dfrac{1}{2}\cdot OH\cdot AB=\dfrac{1}{2}\cdot5\cdot5=12,5\left(đvdt\right)\)
Đúng 1
Bình luận (0)
Cho hàm số y=\(\dfrac{1}{4}x^2\) (P) ; y=\(\dfrac{1}{2}\)x+2 (d)
a,Vẽ (d) và (P) trên cùng mặt phẳng tọa độ
b,Tìm tòa độ giao điểm của (P) và (d)
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+2\)
\(\Leftrightarrow x^2-2x-8=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{1}{4}\cdot4^2=4\\y=\dfrac{1}{4}\cdot\left(-2\right)^2=1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
không vẽ đồ thị hãy tìm tọa độ các giao điểm của các đồ thị hàm số sau:
a) y=x\(^2\)và y=\(\dfrac{1}{2}\)x b) y=\(-\dfrac{1}{2}x^2\)và y=mx+\(\dfrac{1}{2}m^2-8\)
a, Hoành độ giao điểm tm pt
\(x^2-\dfrac{1}{2}x=0\Leftrightarrow x\left(x-\dfrac{1}{2}\right)=0\Leftrightarrow x=0;x=\dfrac{1}{2}\)
Với x = 0 => y = 0
Với x = 1/2 => y = 1/4
Vậy (P) cắt (d) tại O(0;0) ; A(1/2;1/4)
Đúng 0
Bình luận (0)
Cho hàm số y =\(\dfrac{2x-1}{x+2}\) (C) và đường thẳng d : y = mx - 2 . tìm m để (C) cắt d tại hai điểm phân biệt A , B sao cho I ( 2 ;0 ) là trung điểm của AB
1) đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
2) đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
1) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
2) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1\left(x+9\right)}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-6}{\left(x+3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(1\right)=\dfrac{-6}{\left(1+3\right)^2}+\dfrac{2}{\sqrt[]{1}}=-\dfrac{3}{8}+2=\dfrac{13}{8}\)
Đúng 1
Bình luận (0)
Cho hàm số \(y=\dfrac{1}{2}x^2\) có đồ thị thì (P) và đường thẳng (d) có phương trình: \(y=x+1\)
a, Vẽ đồ thị hai hàm số trên cùng một mặt phẳng tọa độ Oxy
b, Tìm tọa độ giao điểm của 2 hàm số trên.
Cho hai hàm số \(y=\dfrac{2}{3}x\) và \(y=x^2-x+\dfrac{2}{3}\)
Tìm tọa độ giao điểm của hai hàm số bằng phép tính
PTHĐGĐ của hai hs:
\(\dfrac{2}{3}x=x^2-x+\dfrac{2}{3}\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{2}{3}\end{matrix}\right.\)
Thay x vào hàm số đầu tiên: \(\left[{}\begin{matrix}y=\dfrac{2}{3}\cdot1=\dfrac{2}{3}\\y=\dfrac{2}{3}\cdot\dfrac{2}{3}=\dfrac{4}{9}\end{matrix}\right.\)
Vậy hai hs cắt nhau tại: \(\left[{}\begin{matrix}A\left(1;\dfrac{2}{3}\right)\\A\left(\dfrac{2}{3};\dfrac{4}{9}\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)



















