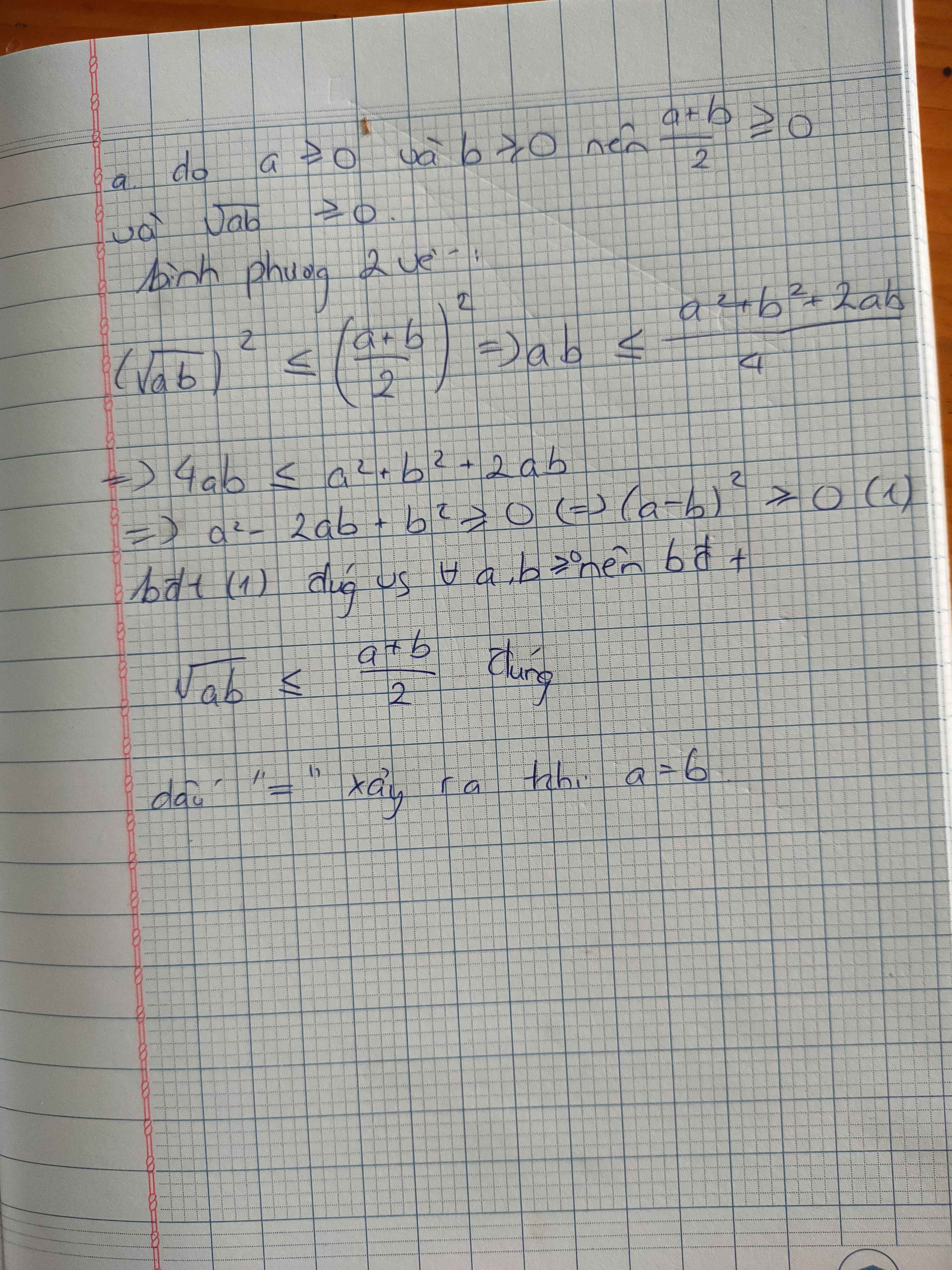Chứng minh bất đẳng thức: Với a, b, c >0

Những câu hỏi liên quan
Chứng minh: Bất đẳng thức: \(a^3+b^3+3abc\ge ab.\left(a+b+c\right)\) với a, b, c>0
Với $a,b,c>0$ thì $a^3+b^3+3abc> ab(a+b+c)$ chứ không có dấu "=" nhé bạn. Còn về cách làm thì bạn Trương Huy Hoàng đã làm rất chi tiết rồi.
Đúng 2
Bình luận (0)
a3 + b3 + 3abc \(\ge\) ab(a + b + c)
\(\Leftrightarrow\) a3 + b3 + 3abc - a2b - ab2 - abc \(\ge\) 0
\(\Leftrightarrow\) a3 + b3 + 2abc - a2b - ab2 \(\ge\) 0
\(\Leftrightarrow\) a2(a - b) - b2(a - b) + 2abc \(\ge\) 0
\(\Leftrightarrow\) (a - b)(a2 - b2) + 2abc \(\ge\) 0
\(\Leftrightarrow\) (a - b)2(a + b) + 2abc \(\ge\) 0 (luôn đúng với mọi a, b, c > 0)
Chúc bn học tốt!
Đúng 2
Bình luận (0)
chứng minh bất đẳng thức a/(a+b)+b/(b+c)+c/(c+a)>=3/2 với a>=b>=c>0
Chứng minh bất đẳng thức
a/(a+b) + b/(b+c) + c/(c+a) >= 3/2 Với a >= b >= c > 0
chứng minh bất đẳng thức : (a/a+b)+(b/b+c)+(c/c+a) >= 3/2 với a>=b>=c>0
\(BDT\Leftrightarrow\left(\frac{a}{a+b}-\frac{1}{2}\right)+\left(\frac{b}{b+c}-\frac{1}{2}\right)+\left(\frac{c}{c+a}-\frac{1}{2}\right)\ge0\)
\(\Leftrightarrow\frac{a-b}{2\left(a+b\right)}+\frac{b-c}{2\left(b+c\right)}+\frac{c-a}{2\left(c+a\right)}\ge0\)
\(\Leftrightarrow\frac{a-b}{2\left(a+b\right)}+\frac{\left(b-a\right)+\left(a-c\right)}{2\left(b+c\right)}+\frac{c-a}{2\left(c+a\right)}\ge0\)
\(\Leftrightarrow\frac{1}{2}\left(a-b\right)\left(\frac{1}{a+b}-\frac{1}{b+c}\right)+\frac{1}{2}\left(a-c\right)\left(\frac{1}{b+c}-\frac{1}{c+a}\right)\ge0\)
\(\Leftrightarrow\frac{\left(c-a\right)\left(a-b\right)}{2\left(a+b\right)\left(b+c\right)}+\frac{\left(a-c\right)\left(a-b\right)}{2\left(b+c\right)\left(c+a\right)}\ge0\)
\(\Leftrightarrow\frac{\left(a-c\right)\left(a-b\right)}{2\left(b+c\right)}\left(-\frac{1}{a+b}+\frac{1}{c+a}\right)\ge0\)
\(\Leftrightarrow\frac{\left(a-c\right)\left(a-b\right)\left(b-c\right)}{2\left(a+b\right)\left(a+c\right)\left(b+c\right)}\ge0\)(luôn đúng \(\forall a\ge b\ge c>0\))
Vậy BĐT đã được chứng minh
Đúng 1
Bình luận (0)
Chứng minh các bất đẳng thức sau:
a) tanx > sinx, 0 < x < π/2
b) 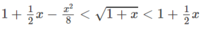
với 0 < x < + ∞
a) Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π/2);

x ∈ [0;1/2)
Dấu “=” xảy ra khi x = 0.
Suy ra f(x) đồng biến trên nửa khoảng [0; π/2)
Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)
b) Xét hàm số h(x) trên [0; + ∞ )
![]()
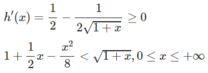
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; + ∞ ).
Vì h(x) = 0 nên
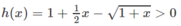
Hay
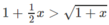
Xét hàm số trên f(x) trên [0; + ∞ );
![]()
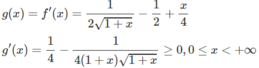
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; + ∞ ) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .
Mặt khác, ta có f(0) = 0 nên
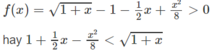
Với mọi 0 < x < + ∞ .
Đúng 0
Bình luận (0)
Chứng minh bất đẳng thức Cô-si
Bất đẳng thức Cô-si cho hai số là:
\(\dfrac{a+b}{2}\) ≥\(\sqrt{ab}\) , a≥0 , b≥0
Giúp với mai mink thi rồi
Ta có : \(\left(a-b\right)^2\ge0\)
\(\Rightarrow a^2+b^2+2ab\ge4ab\)
\(\Leftrightarrow\left(a+b\right)^2\ge4ab\)
Có : \(a,b\ge0\)
\(\Rightarrow a+b\ge2\sqrt{ab}\)
\(\Leftrightarrow\dfrac{a+b}{2}\ge\sqrt{ab}\) ( đpcm )
Vậy ...
Đúng 1
Bình luận (0)
Chứng minh bất đẳng thức;
(a+b).(b+c).(c+a) > 8abc (a,b,c >0)
vì a>0;b>0;c>0\(\Rightarrow\sqrt{a};\sqrt{b};\sqrt{c}\)luôn được xác định
\(\left(\sqrt{a}-\sqrt{b}\right)^2>=0\Rightarrow a-2\sqrt{ab}+b>=0\Rightarrow a+b>=2\sqrt{ab}\)
\(\left(\sqrt{b}-\sqrt{c}\right)^2>=0\Rightarrow b-2\sqrt{bc}+c>=0\Rightarrow b+c>=2\sqrt{bc}\)
\(\left(\sqrt{c}-\sqrt{a}\right)^2>=0\Rightarrow c-2\sqrt{ca}+a>=0\Rightarrow c+a>+2\sqrt{ca}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)>=2\sqrt{ab}\cdot2\sqrt{bc}\cdot2\sqrt{ca}=8\sqrt{a^2b^2c^2}=8abc\)(đpcm)
dấu = xảy ra khi a=b=c
Đúng 0
Bình luận (0)
Áp dụng ĐBT Cauchy - schwarz cho 2 số không âm, ta được:
\(a+b\ge2\sqrt{ab}\)
\(b+c\ge2\sqrt{bc}\)
\(a+c\ge2\sqrt{ac}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\sqrt{\left(abc\right)^2}=8abc\left(đpcm\right)\)
Đúng 0
Bình luận (0)
a) Chứng minh bất đẳng thức (a + 1)2 ≥ 4a
b) Cho a, b, c > 0 và abc = 1. Chứng minh: (a + 1)(b + 1)(c + 1) ≥ 8
help me vs
a) Ta có: \(\left(a-1\right)^2\ge0\forall a\)
\(\Leftrightarrow a^2-2a+1\ge0\forall a\)
\(\Leftrightarrow a^2+2a+1\ge4a\forall a\)
\(\Leftrightarrow\left(a+1\right)^2\ge4a\)(đpcm)
Đúng 1
Bình luận (1)
b) Áp dụng bất đẳng thức Cosi ta có:
\(a+1\ge2\sqrt{a};b+1\ge2\sqrt{b};c+1\ge2\sqrt{c}\\ \Rightarrow\left(a+1\right)\left(b+1\right)\left(c+1\right)\ge8\sqrt{abc}=8\)
Dấu = xảy ra khi và chỉ khi a=b=c=1
Đúng 1
Bình luận (1)
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy: ![]()
b) Cho a, b, c > 0. Chứng minh rằng: ![]()
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab
\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)
Đúng 2
Bình luận (0)