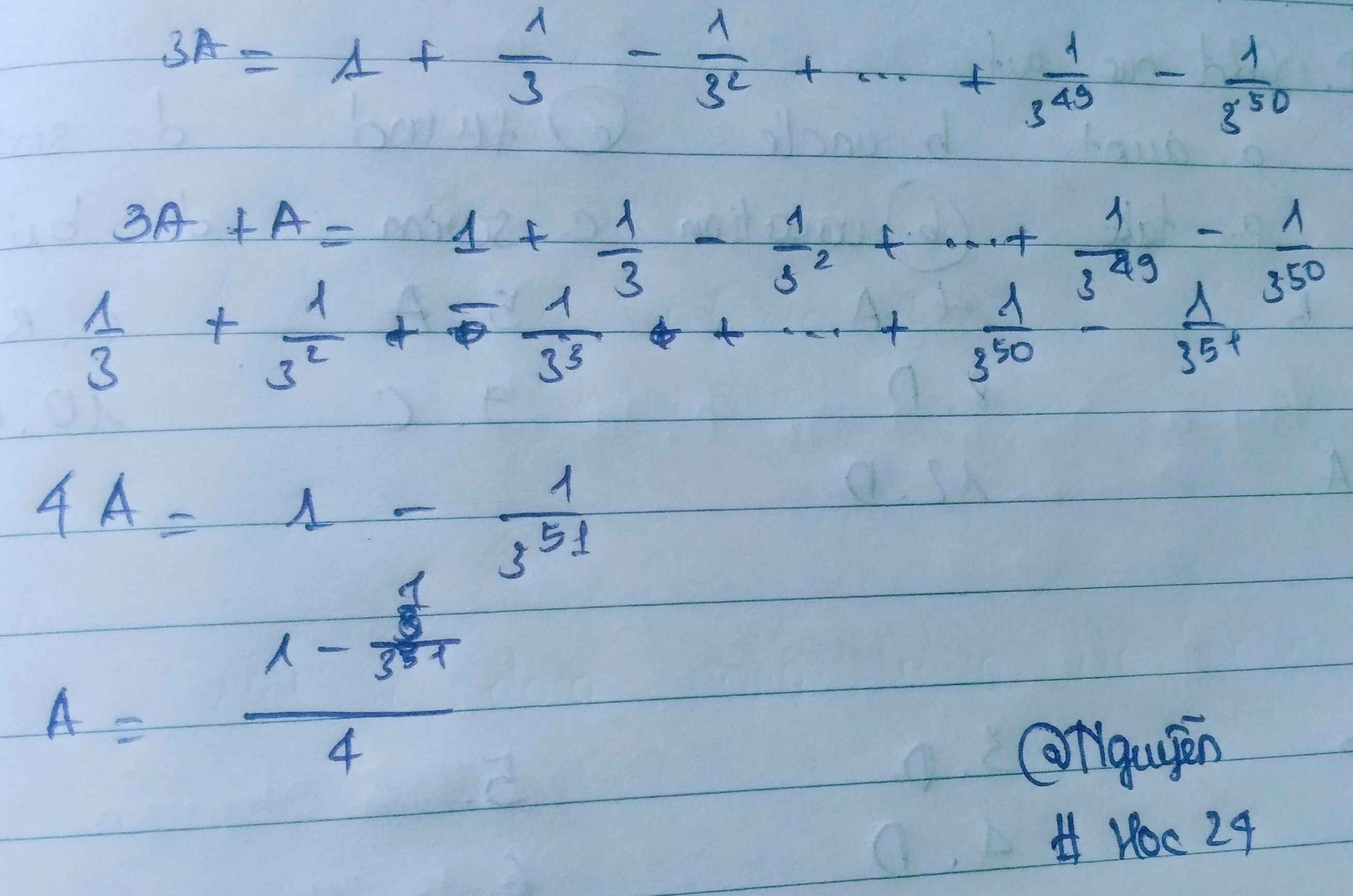a) \(x-25\%x=0,5\)

\(\dfrac{3}{4}x=0,5\)

x = \(\dfrac{2}{3}\)

b) \(\left(50\%x+5\dfrac{1}{4}\right).\dfrac{-2}{3}=2\dfrac{5}{6}\)

\(\left(0,5x+\dfrac{21}{4}\right)=\dfrac{-17}{4}\)

\(0,5x=\dfrac{-19}{2}\)

x = -19

c) \(\left(1\dfrac{1}{3}-25\%-\dfrac{5}{12}\right)+2x=1,5:\dfrac{3}{5}\)

\(\dfrac{2}{3}+2x=\dfrac{5}{2}\)

\(2x=\dfrac{11}{6}\)

x= \(\dfrac{11}{12}\)

a: \(=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{121}-\dfrac{1}{124}=1-\dfrac{1}{124}=\dfrac{123}{124}\)

b: \(=3\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{100}-\dfrac{1}{101}\right)=3\cdot\dfrac{99}{202}=\dfrac{297}{202}\)

c: \(=\dfrac{1}{4}\left(1-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{9}-...+\dfrac{1}{401}-\dfrac{1}{405}\right)=\dfrac{1}{4}\cdot\dfrac{404}{405}=\dfrac{101}{405}\)

d: \(=1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{99}-\dfrac{1}{101}=1-\dfrac{1}{101}=\dfrac{100}{101}\)

đề bài là j

a/ Đặt :

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+.........+\dfrac{1}{3^{50}}\)

\(\Leftrightarrow3A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+.......+\dfrac{1}{3^{49}}\)

\(\Leftrightarrow3A-A=\left(1+\dfrac{1}{3}+....+\dfrac{1}{3^{49}}\right)-\left(\dfrac{1}{3}+\dfrac{1}{3^2}+....+\dfrac{1}{3^{50}}\right)\)

\(\Leftrightarrow2A=1-\dfrac{1}{3^{50}}\)

còn sao nx thì mk chịu =.=

Ta có :

Vế phải =1 - 1/2 + 1/3 - 1/4 + ... + 1/49 - 1/50

= (1+ 1/3 + 1/5 + ... + 1/49) - (1/2 + 1/4 + ... +1/50)

<=> (1 + 1/2 + 1/3 + 1/4 + ... + 1/49+1/50)- 2(1/2 +1/4 +...+1/50)

=(1+1/2 +1/3 +1/4...+ 1/49+1/50) - (1+1/2 +...+1/25)

=1/26 + 1/27 +1/28 +...+1/50 (đpcm)

\(B=\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{50}}-\dfrac{1}{3^{51}}\)

\(=\dfrac{1}{\left(-3\right)}+\dfrac{1}{\left(-3\right)^2}+\dfrac{1}{\left(-3\right)^3}+...+\dfrac{1}{\left(-3\right)^{50}}+\dfrac{1}{\left(-3\right)^{51}}-\dfrac{1}{3}\)

\(=\dfrac{1}{\left(3\right)^2}+\dfrac{1}{\left(3\right)^3}+...+\dfrac{1}{\left(-3\right)^{51}}+\dfrac{1}{\left(-3\right)^{52}}\)

\(\Rightarrow\dfrac{4}{3}B=\dfrac{1}{-3}-\dfrac{1}{\left(-3\right)^{52}}=\dfrac{-3^{51}-1}{3^{52}}\Rightarrow B=\dfrac{-3^{51}-1}{4.3^{51}}\)

\(a,=\dfrac{13}{50}\cdot\dfrac{50}{13}\cdot\left(-\dfrac{31}{2}\right)\cdot\dfrac{169}{2}=-\dfrac{5239}{2}\\ b,=\dfrac{-\dfrac{49}{100}\cdot\left(-125\right)}{-\dfrac{343}{27}\cdot\dfrac{81}{16}\cdot\left(-1\right)}=\dfrac{\dfrac{245}{4}}{\dfrac{1029}{16}}=\dfrac{245}{4}\cdot\dfrac{16}{1029}=\dfrac{20}{21}\)

a) \(\dfrac{13}{50}.\left(-15.5\right):\dfrac{13}{50}.84\dfrac{1}{2}=\dfrac{13}{50}.-75:\dfrac{13}{50}.\dfrac{169}{2}=-\dfrac{75.169}{2}=-\dfrac{12675}{2}\)

b) \(\dfrac{\left(-0,7\right)^2.\left(-5\right)^3}{\left(-2\dfrac{1}{3}\right)^3.\left(1\dfrac{1}{2}\right)^4.\left(-1\right)^5}=\dfrac{0,49.\left(-125\right)}{-\dfrac{343}{27}.\dfrac{81}{16}.\left(-1\right)}=-\dfrac{\dfrac{245}{4}}{\dfrac{1029}{16}}=\dfrac{20}{21}\)

\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{50}}\)

\(3.A=1+\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{49}}\)

\(2A=3A-A=1-\dfrac{1}{3^{49}}\)

\(\Rightarrow A=\dfrac{1-\dfrac{1}{3^{50}}}{2}\)

\(B=\dfrac{5}{3}+\dfrac{5}{3^2}+...+\dfrac{5}{3^{50}}=5\left(\dfrac{1}{3}+\dfrac{1}{3^2}+...+\dfrac{1}{3^{50}}\right)\)

Căn cứ vào câu A thì các trong ngặc bằng \(\dfrac{1-\dfrac{1}{3^{50}}}{2}\)

suy ra \(B=\dfrac{5\left(1-\dfrac{1}{3^{50}}\right)}{2}\)

tick mik nha

hoi kho day

\(C=-\left[\dfrac{1}{3}\cdot\dfrac{\left(3+1\right)\cdot3}{2}+\dfrac{1}{4}\cdot\dfrac{\left(4+1\right)\cdot4}{2}+...+\dfrac{1}{50}\cdot\dfrac{\left(50+1\right)\cdot50}{2}\right]\\ C=-\left(\dfrac{1}{3}\cdot\dfrac{4\cdot3}{2}+\dfrac{1}{4}\cdot\dfrac{5\cdot4}{2}+...+\dfrac{1}{50}\cdot\dfrac{51\cdot50}{2}\right)\\ C=-\left(2+\dfrac{5}{2}+...+\dfrac{51}{2}\right)\\ C=-\dfrac{4+5+...+51}{2}=-\dfrac{\dfrac{\left(51+4\right)\left(51-4+1\right)}{2}}{2}=-\dfrac{55\cdot48}{4}=-660\)