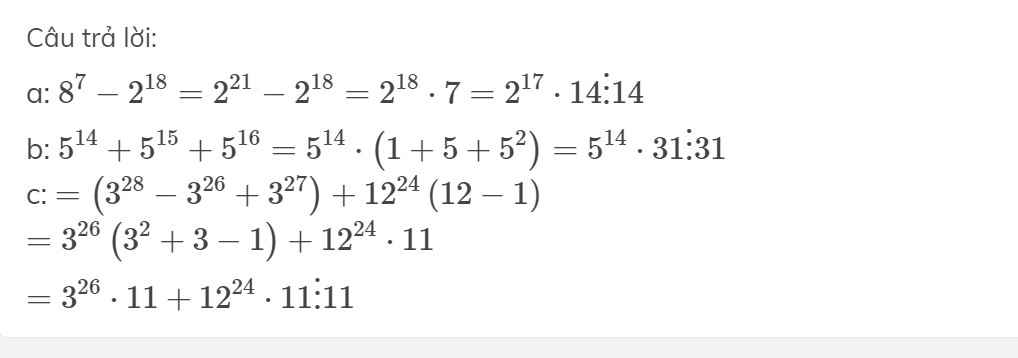\(M=2^{2010}-\left(2^{2009}+2^{2008}+...+2^1+2^0\right)\)
Bài 5: Lũy thừa của một số hữu tỉ
Đặt \(A=2^{2009}+2^{2008}+...+2+2^0\)
\(=1+2+...+2^{2008}+2^{2009}\)
\(\Rightarrow2A=2+2^2+...+2^{2010}\)
\(\Rightarrow2A-A=\left(2+2^2+...+2^{2010}\right)-\left(1+2+...+2^{2009}\right)\)
\(\Rightarrow A=2^{2010}-1\)
\(\Rightarrow M=2^{2010}-\left(2^{2010}-1\right)\)
\(=2^{2010}-2^{2010}+1=1\)
Vậy M = 1
Đúng 0
Bình luận (0)
Bài 1:Tính
a)left(dfrac{3}{7}+dfrac{1}{2}right)^2 b)left(dfrac{3}{4}-dfrac{5}{6}right)^2c) dfrac{5^4.20^4}{25^5.4^5}
Bài 2:Tìm x
a)left(x-dfrac{1}{5}right)^{2004}+left(y+0,4right)^{100}+left(z-3right)^{678}0
b)left(x+5right)^3-64 c)left(2x-3right)^29
c)x^2+182
Bài 3:Tính
Mdfrac{8^{10}+4^{10}}{8^4+4^{11}}
Bài 4:So sánh 2^{24}và3^{16}
GIÚP MIK DZỚI,MÌNH TIK CHO
Đọc tiếp
Bài 1:Tính
a)\(\left(\dfrac{3}{7}+\dfrac{1}{2}\right)^2\) b)\(\left(\dfrac{3}{4}-\dfrac{5}{6}\right)^2\)c) \(\dfrac{5^4.20^4}{25^5.4^5}\)
Bài 2:Tìm x
a)\(\left(x-\dfrac{1}{5}\right)^{2004}+\left(y+0,4\right)^{100}+\left(z-3\right)^{678}=0\)
b)\(\left(x+5\right)^3=-64\) c)\(\left(2x-3\right)^2=9\)
c)\(x^2+1=82\)
Bài 3:Tính
M=\(\dfrac{8^{10}+4^{10}}{8^4+4^{11}}\)
Bài 4:So sánh \(2^{24}\)và\(3^{16}\)
GIÚP MIK DZỚI,MÌNH TIK CHO ><
Bài 1:
c) \(\dfrac{5^4.20^4}{25^5.4^5}=\dfrac{5^4.4^4.5^4}{5^{10}.4^5}=\dfrac{5^8.4^4}{5^8.5^2.4^4.4}=\dfrac{1}{25.4}=\dfrac{1}{100}\)
Bài 2: a) \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{5}\right)^{2004}\ge0\forall x\\\left(y+0,4\right)^{100}\ge0\forall y\\\left(z-3\right)^{678}\ge0\forall z\end{matrix}\right.\) \(\Rightarrow\left(x-\dfrac{1}{5}\right)^{2004}+\left(y+0,4\right)^{100}+\left(z-3\right)^{678}\ge0\forall x,y,z\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}\left(x-\dfrac{1}{5}\right)^{2004}=0\\\left(y+0,4\right)^{100}=0\\\left(z-3\right)^{678}=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{5}\\y=-\dfrac{2}{5}\\z=3\end{matrix}\right.\)
Vậy ...
Bài 3: \(M=\dfrac{8^{10}+4^{10}}{8^4+4^{11}}=\dfrac{\left(2^3\right)^{10}+\left(2^2\right)^{10}}{\left(2^3\right)^4+\left(2^2\right)^{11}}=\dfrac{2^{30}+2^{20}}{2^{12}+2^{22}}\)
\(=\dfrac{2^{20}\left(2^{10}+1\right)}{2^{12}\left(2^{10}+1\right)}=\dfrac{2^{20}}{2^{12}}=2^8=256.\)
Vậy \(M=256.\)
Mấy bài kia dễ tự làm.
Đúng 0
Bình luận (2)
\(3)\)
\(\dfrac{8^{10}+4^{10}}{8^4+4^{11}}=\dfrac{\left(2^3\right)^{10}+\left(2^2\right)^{10}}{\left(2^3\right)^4+\left(2^2\right)^{11}}=\dfrac{2^{30}+2^{20}}{2^{12}+2^{22}}=\dfrac{2^{20}\left(2^{10}+1\right)}{2^{12}\left(2^{10}+1\right)}=\dfrac{2^{20}}{2^{12}}=2^8=256\)\(4)\)
\(2^{24}=\left(2^6\right)^4=64^4;3^{16}=\left(3^4\right)^4=81^4\)
\(\Leftrightarrow2^{24}< 3^{16}\)
Đúng 0
Bình luận (0)
Bài 4 :
\(2^{24}=\left(2^3\right)^8=8^8\) \(\left(1\right)\)
\(3^{16}=\left(3^2\right)^8=9^8\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow8^8< 9^8\)
hay \(2^{24}< 3^{16}\) \((dpcm) \)
Đúng 0
Bình luận (0)
chứng minh rằng
\(^{8^7-2^{18}}chia\) \(hết\) cho 14
giải cụ thể nha
Ta có :
\(8^7-2^{18}=\left(2^3\right)^7-2^{18}\)
\(=2^{21}-2^{18}\)
\(=2^{18}\left(2^3-1\right)\)
\(=2^{18}.7\)
\(=2^{17}.2.7\)
\(=2^{17}.14⋮14\)
Vậy \(8^7-2^{18}⋮14\rightarrowđpcm\)
Đúng 0
Bình luận (0)
Ta có:
\(8^7-2^{18}=\left(2^3\right)^7-2^{18}\)
\(=2^{21}-2^{18}=2^{18}.\left(2^3-1\right)\)
\(=2^{17}.2.7=2^{17}.14\)
Vì \(14⋮14\) nên \(2^{17}.14⋮14\)
=> \(8^7-2^{18}⋮14\) (đpcm)
Chúc bạn học tốt!!!
Đúng 0
Bình luận (0)
Giải:
\(8^7-2^{18}\)
\(=\left(2^3\right)^7-2^{18}\)
\(=2^{21}-2^{18}\)
\(=2^{18}.\left(2^3-1\right)\)
\(=2^{18}.\left(8-1\right)\)
\(=2^{18}.7\)
\(=2^{17}.2.7\)
\(=2^{17}.14⋮14\) (đpcm)
Chúc bạn học tốt!![]()
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
so sánh
\(2^{91}-5^{35}\)
giải cụ thể nha
C1: Ta có: \(2^{91}=\left(2^{13}\right)^7\)
\(5^{35}=\left(5^5\right)^7\)
Do \(2^{13}>5^5\Rightarrow2^{91}>5^{35}\)
cách trên thửu công quá nên ta có cách khác tìm số trung gian,
C2: \(2^{91}>2^{90}=\left(2^5\right)^{18}=32^{18}\left(1\right)\)
\(5^{35}< 5^{36}=\left(5^2\right)^{18}=25^{18}\left(2\right)\)
Do \(32>25\Rightarrow32^2>25^2\left(3\right)\)
Từ (1);(2);(3) Suy ra:
\(2^{91}>5^{35}\)
Đúng 0
Bình luận (0)
tìm x: (1/2 - 1/3) . 6^x + 6^x+2 = 6^10 + 6^7
lm ơn giúp mifh vs ạ
\(\Leftrightarrow6^x\cdot\dfrac{1}{6}+6^x\cdot36=6^7\cdot217\)
\(\Leftrightarrow6^x=1679616\)
hay x=8
Đúng 0
Bình luận (0)
chứng minh rằng
3/1^2.2^2+5/2^2.3^2+7/3^2.4^2+.....+19/9^2.10^2<1
\(\dfrac{3}{1^2.2^2}+\dfrac{5}{2^2.3^2}+...+\dfrac{19}{9^{10}.10^2}\)
\(=\dfrac{1}{1^2}-\dfrac{1}{2^2}+\dfrac{1}{2^2}-\dfrac{1}{3^2}+...+\dfrac{1}{9^{10}}-\dfrac{1}{10^2}\)
\(=1-\dfrac{1}{10^2}< 1\)
\(\Rightarrowđpcm\)
Đúng 1
Bình luận (1)
chứng tỏ: 8^7 - 2^18 chia hết cho 14.
b) 5^14 . 5^15 . 5^16 chia hết cho 31
c) 81^7 - 9^13 +12^25 + 27^9 - 12^24 chia hết cho 11.
Làm giúp mình nha mình cần gấp, ai làm nhanh tick cho
cám ơn trước
chứng tỏ: 8^7 - 2^18 chia hết cho 14. b) 5^14 . 5^15 . 5^16 chia hết cho 31 c) 81^7 - 9^13 +12^25 + 27^9 - 12^24 chia hết cho 11....
Đọc tiếp
chứng tỏ: 8^7 - 2^18 chia hết cho 14. b) 5^14 . 5^15 . 5^16 chia hết cho 31 c) 81^7 - 9^13 +12^25 + 27^9 - 12^24 chia hết cho 11. Làm giúp mình nha mình cần gấp, ai làm nhanh tick
Đọc thêm Toán lớp 7
ta có
\(8^7-2^{18}=8^7-\left(2^3\right)^6\\ =8^7-8^6=8^6\left(8-1\right)\\ =8^6.7=8^5.8.7=8^5.\left(4.2\right).7=14.\left(4.8^5\right)\)
do 14 chia hết cho 14 nên \(14.\left(4.8^5\right)\)cũng chia hết cho 14
hay\(8^7-2^{18}\)chia hết cho 14
các câu b,c bạn làm tương tự. mình chỉ làm cho bạn câu a. chúc bạn học tốt. nếu có vấn đề j về bài toán câu a thì bạn cứ ib cho mình mình sẽ giải đáp.
Đúng 0
Bình luận (1)
Tính M=\(2^{2010}-(2^{2009}+2^{2008}+...+2^1+2^0)\)
\(M=2^{2010}-\left(2^{2009}+2^{2008}+...+2^1+2^0\right)\)
Gọi \(N=2^{2009}+2^{2008}+...+2^1+2^0\)
\(2N=2^{2010}+2^{2009}+...+2^2+2^1\\ 2N-N=\left(2^{2010}+2^{2009}+...+2^2+2^1\right)-\left(2^{2009}+2^{2008}+...+2^1+2^0\right)\\ N=2^{2010}-2^0\\ N=2^{2010}-1\)
Thay vào ta được
\(M=2^{2010}-\left(2^{2010}-1\right)\\ M=2^{2010}-2^{2010}+1\\ M=1\)
Vậy \(M=1\)
Đúng 0
Bình luận (0)
Ta có :
\(M=2^{2010}-\left(2^{2009}+2^{2008}+...+2^0\right)\)
Đặt A=22009+22008+..+20
\(A=2^{2009}+2^{2008}+...+2^0\\ 2A=2^{2010}+2^{2009}+...+2^1\\ \Rightarrow2A-A=A=2^{2010}-2^0\\ \Rightarrow M=2^{2010}-\left(2^{2010}-2^0\right)\\ M=2^{2010}-2^{2010}+1\\ \Rightarrow M=1\)
Chúc bạn học tốt!![]()
Đúng 0
Bình luận (0)
Chứng minh biểu thức không là số nguyên:
C = 32 + 3 + \(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{20}}\)