Bài 7: Tỉ lệ thức
Nội dung lý thuyết
1. Định nghĩa
Xét các ví dụ sau:
+) Ta có \(\dfrac{12}{16}=\dfrac{3}{4}\); \(\dfrac{0,45}{0,6}=\dfrac{45}{60}=\dfrac{3}{4}\). Do đó \(\dfrac{12}{16}=\dfrac{0,45}{0,6}\).
Ta nói đẳng thức \(\dfrac{12}{16}=\dfrac{0,45}{0,6}\) là một tỉ lệ thức.
+) Lại có \(1\dfrac{1}{3}:2\dfrac{5}{6}=\dfrac{4}{3}:\dfrac{17}{6}=\dfrac{8}{17}\); \(1,6:3,4=\dfrac{1,6}{3,4}=\dfrac{16}{34}=\dfrac{8}{17}\). Do đó \(1\dfrac{1}{3}:2\dfrac{5}{6}=1,6:3,4\).
Ta nói đẳng thức \(1\dfrac{1}{3}:2\dfrac{5}{6}=1,6:3,4\) cũng là một tỉ lệ thức.
Một cách tổng quát, ta có định nghĩa:
Định nghĩa: Tỉ lệ thức là đẳng thức của hai tỉ số \(\dfrac{a}{b}=\dfrac{c}{d}\).
Chú ý: Tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) còn được viết là \(a:b=c:d\).
Ghi nhớ: Trong tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\)
- Các số \(a,b,c,d\) được gọi là các số hạng của tỉ lệ thức.
- \(a,d\) là các số hạng ngoài hay ngoại tỉ.
- \(b,c\) là các số hạng trong hay trung tỉ.
Lưu ý: Cần phân biệt rõ ngoại tỉ và trung tỉ dựa theo vị trí của các số hạng trong tỉ lệ thức.
Ví dụ 1: \(\dfrac{2}{3}=\dfrac{-6}{-9}\), \(\dfrac{0,25}{1,25}=\dfrac{-0,4}{-2}\), \(3:5=1,5:2,5\), ... là các tỉ lệ thức.
Ví dụ 2: Kiểm tra các tỉ số sau đây có lập được tỉ lệ thức hay không. Nếu có hãy chỉ ra ngoại tỉ và trung tỉ của nó.
a) \(-3,5:4,2\) và \(\dfrac{5}{3}:\left(-2\right)\);
b) \(-3\dfrac{1}{2}:7\) và \(-2\dfrac{2}{5}:7\dfrac{1}{5}\).
Lời giải:
a) Ta có \(-3,5:4,2=\dfrac{-3,5}{4,2}=\dfrac{-35}{42}=\dfrac{-5}{6}\); \(\dfrac{5}{3}:\left(-2\right)=\dfrac{5}{3}.\dfrac{-1}{2}=\dfrac{-5}{6}\)
Suy ra \(-3,5:4,2=\dfrac{5}{3}:\left(-2\right)\).
Do đó từ hai tỉ số \(-3,5:4,2\) và \(\dfrac{5}{3}:\left(-2\right)\), ta lập được tỉ lệ thức. Trong đó: \(-3,5\) và \(-2\) là các ngoại tỉ, \(4,2\) và \(\dfrac{5}{3}\) là các trung tỉ.
b) Ta có \(-3\dfrac{1}{2}:7=\dfrac{-7}{2}:7=\dfrac{-1}{2}\); \(-2\dfrac{2}{5}:7\dfrac{1}{5}=\dfrac{-12}{5}:\dfrac{36}{5}=\dfrac{-12}{36}=\dfrac{-1}{3}\).
Do \(\dfrac{-1}{2}\ne\dfrac{-1}{3}\) nên ta không lập được tỉ lệ thức từ hai tỉ số \(-3\dfrac{1}{2}:7\) và \(-2\dfrac{2}{5}:7\dfrac{1}{5}\).
2. Tính chất
Tính chất 1 (Tính chất cơ bản của tỉ lệ thức)
Xét tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\). Bằng cách nhân hai tỉ số trong tỉ lệ thức này với tích \(b.d\), ta có:
\(\dfrac{a}{b}.b.d=\dfrac{c}{d}.b.d\)
Suy ra \(a.d=b.c\).
Kết quả này không phụ thuộc vào cách ta chọn các tỉ số trong tỉ lệ thức. Do đó, ta có tính chất sau:
Tính chất: Nếu \(\dfrac{a}{b}=\dfrac{c}{d}\) thì \(a.d=b.c\).
Ví dụ: \(\dfrac{32}{14}=\dfrac{64}{28}\), suy ra \(32.28=64.14\).
Ta thường sử dụng tính chất cơ bản của tỉ lệ thức trong một số bài toán tìm \(x\), chẳng hạn:
Ví dụ: Tìm số hữu tỉ \(x\) thỏa mãn:
a) \(\dfrac{x}{13}=\dfrac{-3}{52}\);
b) \(\dfrac{x}{16}=\dfrac{4}{x}\);
c) \(\dfrac{2x-5}{-3}=\dfrac{-7}{4}\).
Lời giải:
a) Ta có \(\dfrac{x}{13}=\dfrac{-3}{52}\). Theo tính chất cơ bản của tỉ lệ thức:
\(x.52=13.\left(-3\right)\)
Suy ra \(x=\dfrac{13.\left(-3\right)}{52}=\dfrac{13.\left(-3\right)}{13.4}=\dfrac{-3}{4}.\)
Vậy \(x=\dfrac{-3}{4}\) là giá trị cần tìm.
b) Ta có \(\dfrac{x}{16}=\dfrac{4}{x}\). Theo tính chất cơ bản của tỉ lệ thức:
\(x.x=16.4\) hay \(x^2=64=8^2=\left(-8\right)^2\)
Suy ra \(x=8\) hoặc \(x=-8\).
Vậy \(x=8;x=-8\) là các giá trị cần tìm.
c) Ta có \(\dfrac{2x-5}{-3}=\dfrac{-7}{4}\). Theo tính chất cơ bản của tỉ lệ thức:
\(4\left(2x-5\right)=\left(-7\right)\left(-3\right)\)
\(8x-20=21\)
\(8x=41\)
\(x=\dfrac{41}{8}.\)
Vậy \(x=\dfrac{41}{8}\) là giá trị cần tìm.
@884946@
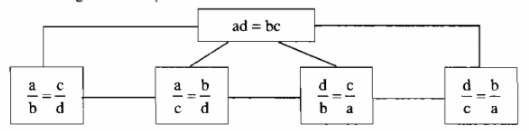
Tính chất 2:
Xét đẳng thức \(ad=bc\) với \(a,b,c,d\ne0\). Bằng cách chia cả hai vế của đẳng thức cho tích \(bd\), ta có:
\(\dfrac{ad}{bd}=\dfrac{bc}{bd}\) hay \(\dfrac{a}{b}=\dfrac{c}{d}\).
Một cách tương tự, từ đẳng thức \(ad=bc\), ta có thể suy ra: \(\dfrac{a}{c}=\dfrac{b}{d};\dfrac{d}{c}=\dfrac{b}{a};\dfrac{d}{b}=\dfrac{c}{a}\).
Tính chất: Nếu \(ad=bc\) và \(a,b,c,d\ne0\) thì ta có các tỉ lệ thức:
\(\dfrac{a}{b}=\dfrac{c}{d};\dfrac{a}{c}=\dfrac{b}{d};\dfrac{d}{c}=\dfrac{b}{a};\dfrac{d}{b}=\dfrac{c}{a}.\)
Ví dụ 1: Ta có \(4.\left(-5\right)=\left(-2\right).10\), do đó ta có các tỉ lệ thức:
\(\dfrac{4}{-2}=\dfrac{10}{-5};\dfrac{4}{10}=\dfrac{-2}{-5};\dfrac{-5}{-2}=\dfrac{10}{4};\dfrac{-5}{10}=\dfrac{-2}{4}.\)
Ví dụ 2: Từ bốn số \(3;5;15;25\) có thể lập được những tỉ lệ thức nào?
Lời giải
Ta có \(3.25=75;5.15=75\), suy ra \(3.25=5.15\).
Do đó, các tỉ lệ thức có thể lập được là:
\(\dfrac{3}{5}=\dfrac{15}{25};\dfrac{3}{15}=\dfrac{5}{25};\dfrac{25}{5}=\dfrac{15}{3};\dfrac{25}{15}=\dfrac{5}{3}\).
Như vậy, với \(a,b,c,d\ne0\), từ một trong năm đẳng thức dưới đây ta có thể suy ra được đẳng thức còn lại:
@884037@