Giúp mình câu c, d, e với ạ

Những câu hỏi liên quan
 giúp mình làm bài 1 câu c,d ,e với ạ
giúp mình làm bài 1 câu c,d ,e với ạ
Đây là nội dung của bài 1 câu c, d, e:
**Câu c:**
\[
\begin{cases}
2x - 3y = 11 \\
-4x + 6y = 5
\end{cases}
\]
**Câu d:**
\[
\begin{cases}
3x + 2y = 1 \\
2x - y = 3
\end{cases}
\]
**Câu e:**
\[
\begin{cases}
2x + 5y = 2 \\
6x - 15y = 6
\end{cases}
\]
3: \(\begin{cases}2x-3y=11\\ -4x+6y=5\end{cases}\Rightarrow\begin{cases}4x-6y=22\\ -4x+6y=5\end{cases}\)
=>\(\begin{cases}4x-6y-4x+6y=22+5\\ 2x-3y=11\end{cases}\Rightarrow\begin{cases}0x=27\\ 2x-3y=11\end{cases}\)
=>(x;y)∈∅
4: \(\begin{cases}3x+2y=1\\ 2x-y=3\end{cases}\Rightarrow\begin{cases}3x+2y=1\\ 4x-2y=6\end{cases}\)
=>\(\begin{cases}3x+2y+4x-2y=1+6=7\\ 2x-y=3\end{cases}\Rightarrow\begin{cases}7x=7\\ y=2x-3\end{cases}\)
=>\(\begin{cases}x=1\\ y=2\cdot1-3=2-3=-1\end{cases}\)
5: \(\begin{cases}2x+5y=2\\ 6x-15y=6\end{cases}\Rightarrow\begin{cases}6x+15y=6\\ 6x-15y=6\end{cases}\)
=>\(\begin{cases}6x+15y+6x-15y=6+6=12\\ 2x+5y=2\end{cases}=.\begin{cases}12x=12\\ 5y=2-2x\end{cases}\)
=>\(\begin{cases}x=1\\ 5y=2-2\cdot1=0\end{cases}\Rightarrow\begin{cases}x=1\\ y=0\end{cases}\)
Đúng 0
Bình luận (0)
Giúp mình câu d và câu e với ạ

d: Xét ΔABC có
BK,CH là đường cao
BK cắt CH tại I
=>I là trực tâm
=>AI vuông góc BC
mà HF vuông góc BC
nên AI//HF
e: Xét ΔABC cân tại A có góc BAC=60 độ
nên ΔABC đều
Xét ΔABC đều có I là trực tâm
nên I là tâm đường tròn ngoại tiếp ΔABC
=>IA=IB=IC
Đúng 0
Bình luận (0)
Các bạn giúp mình câu b;c;d;e ạ. Các bạn làm được câu nào thì làm ạ, còn bạn nào giỏi giúp mình nhiều hơn thì tốt ạ! 
a: Chọn mp(SAC) có chứa AN
Gọi O là giao điểm của AC và BD
Ta có: ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
O∈AC⊂(SAC)
O∈BD⊂(SBD)
Do đó: O∈(SAC) giao (SBD)(1)
S∈(SAC)
S∈(SBD)
Do đó: S∈(SAC) giao (SBD)(2)
Từ (1),(2) suy ra (SAC) giao (SBD)=SO
Gọi I là giao điểm của SO và AN
=>I là giao điểm của AN và mp(SBD)
Xét ΔSAC có
SO,AN là các đường trung tuyến
SO cắt AN tại I
Do đó: I là trọng tâm của ΔSAC
=>\(\frac{IN}{IA}=\frac12\)
b: Chọn mp(ANB) có chứa NM
I∈AN⊂(ANB)
I∈SO⊂(SBD)
Do đó: I∈(ANB) giao (SBD)(3)
B∈(ANB)
B∈(SBD)
Do đó: B∈(ANB) giao (SBD)(4)
Từ (3),(4) suy ra (ANB) giao (SBD)=BI
Gọi K là giao điểm của MN và BI
=>K là giao điểm của MN và (SBD)
c: Vì K là giao điểm của MN và BI
nên B,K,I thẳng hàng
Đúng 0
Bình luận (0)
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
Đọc tiếp
giúp mình bài 6 với ạ trừ câu a còn các câu b,c,d, giúp mình với ạ
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Đúng 4
Bình luận (0)
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
Đúng 1
Bình luận (0)
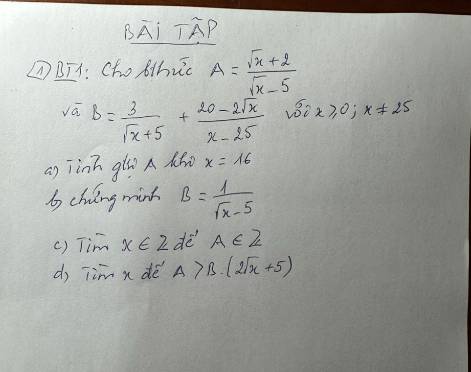
giải giúp mình câu C với câu D với ạ
a) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}-5\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\sqrt[]{x}\ne5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
Khi \(x=16\Rightarrow A=\dfrac{\sqrt[]{16}+2}{\sqrt[]{16}-5}=\dfrac{4+2}{4-5}=-6\)
b) \(B=\dfrac{3}{\sqrt[]{x}+5}+\dfrac{20-2\sqrt[]{x}}{x-25}\)
B có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x-25\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\x\ne25\end{matrix}\right.\)
\(\Leftrightarrow B=\dfrac{3\left(\sqrt[]{x}-5\right)+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{3\sqrt[]{x}-15+20-2\sqrt[]{x}}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{\sqrt[]{x}+5}{\left(\sqrt[]{x}+5\right)\left(\sqrt[]{x}-5\right)}\)
\(\Leftrightarrow B=\dfrac{1}{\sqrt[]{x}-5}\left(dpcm\right)\)
c) \(A=\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}\in Z\left(x\in Z\right)\)
\(\Leftrightarrow\sqrt[]{x}+2⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\left(\sqrt[]{x}-5\right)⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}+2-\sqrt[]{x}+5⋮\sqrt[]{x}-5\)
\(\Leftrightarrow7⋮\sqrt[]{x}-5\)
\(\Leftrightarrow\sqrt[]{x}-5\in U\left(7\right)=\left\{-1;1;-7;7\right\}\)
\(\Leftrightarrow x\in\left\{16;36;144\right\}\)
d) \(A>B\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\dfrac{\sqrt[]{x}+2}{\sqrt[]{x}-5}>\dfrac{1}{\sqrt[]{x}-5}\left(2\sqrt[]{x}+5\right)\)
\(\Leftrightarrow\sqrt[]{x}+2>2\sqrt[]{x}+5\)
\(\Leftrightarrow\sqrt[]{x}< -3\)
mà \(\sqrt[]{x}\ge0\)
\(\Leftrightarrow x\in\varnothing\)
Đúng 2
Bình luận (0)
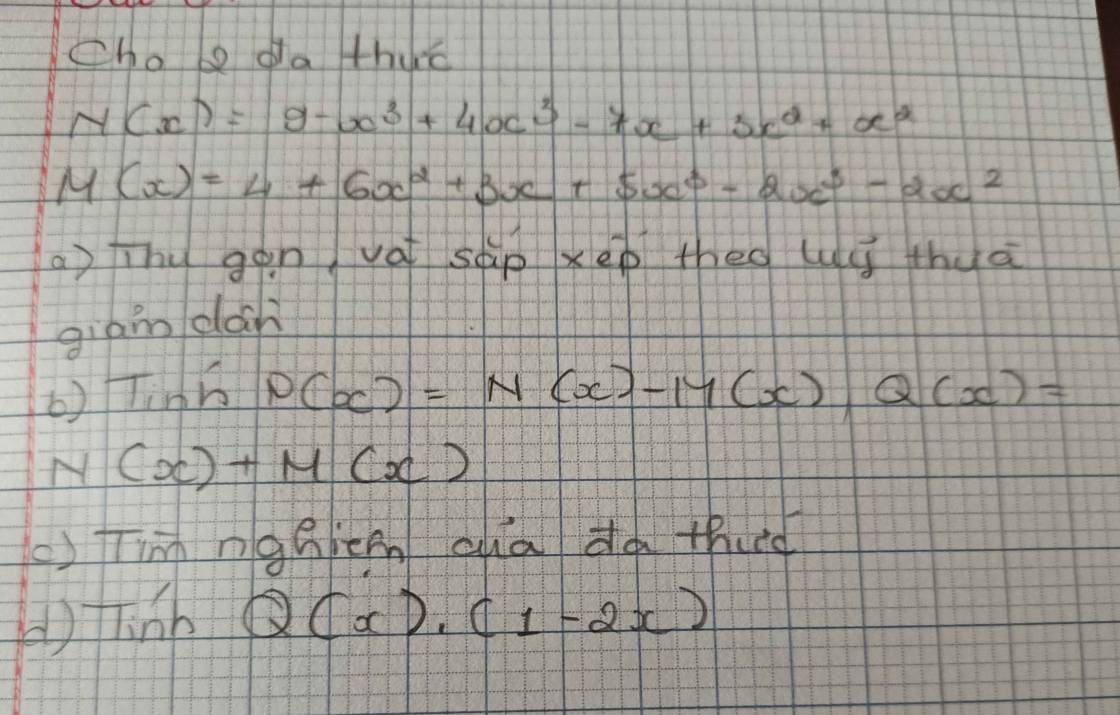 giúp e câu c,d với ạ
giúp e câu c,d với ạ
a) \(N\left(x\right)=9-x^3+4x^3-7x+3x^2+x^2\)
\(N\left(x\right)=-\left(x^3-4x^3\right)+\left(3x^2+x^2\right)-7x+9\)
\(N\left(x\right)=3x^3+4x^2-7x+9\)
\(M\left(x\right)=4+6x^2+3x+5x^3-2x^3-2x^2\)
\(M\left(x\right)=\left(5x^3-2x^3\right)+\left(6x^2-2x^2\right)+3x+4\)
\(M\left(x\right)=3x^3+4x^2+3x+4\)
b) \(P\left(x\right)=N\left(x\right)-M\left(x\right)\)
\(P\left(x\right)=\left(3x^3+4x^2-7x+9\right)-\left(3x^2+4x^2+3x+4\right)\)
\(P\left(x\right)=3x^3+4x^2-7x+9-3x^3-4x^2-3x-4\)
\(P\left(x\right)=-10x+5\)
\(Q\left(x\right)=N\left(x\right)+M\left(x\right)\)
\(Q\left(x\right)=\left(3x^3+4x^2-7x+9\right)+\left(3x^3+4x^2+3x+4\right)\)
\(Q\left(x\right)=3x^3+4x^2-7x+9+3x^3+4x^2+3x+4\)
\(Q\left(x\right)=6x^3+8x^2-4x+13\)
c) Nghiệm của đa thức \(P\left(x\right)\)
\(P\left(x\right)=-10x+5=0\)
\(\Rightarrow-10x=-5\)
\(\Rightarrow10x=5\)
\(\Rightarrow x=\dfrac{5}{10}=\dfrac{1}{2}\)
Nghiệm của đa thức \(Q\left(x\right)\)
Vì: \(Q\left(x\right)=6x^3+8x^2+4x+13\ge0\)
\(\Rightarrow Q\left(x\right)\ge0\)
Vậy đa thức vô nghiệm
d) \(Q\left(x\right)\left(1-2x\right)\)
\(=\left(6x^3+8x^2-4x+13\right)\left(1-2x\right)\)
\(=6x^3+8x^2-4x+13-12x^4-16x^3+8x^2-26x\)
\(=-12x^4-10x^3+16x^2-30x+13\)
Đúng 2
Bình luận (1)
Giúp mình trả câu e và câu d. Mình cảm ơn ạ
d. \(\dfrac{\pi}{2}< a;b< \pi\Rightarrow sina>0;sinb>0\)
\(sina=\sqrt{1-cos^2a}=\dfrac{4}{5}\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{4}{3}\)
\(sinb=\sqrt{1-cos^2b}=\dfrac{5}{13}\Rightarrow tanb=-\dfrac{5}{12}\)
Vậy:
\(sin\left(a-b\right)=sina.cosb-cosa.sinb=\dfrac{4}{5}.\left(-\dfrac{12}{13}\right)-\left(-\dfrac{3}{5}\right)\left(\dfrac{5}{13}\right)=...\)
\(cos\left(a-b\right)=cosa.cosb-sina.sinb=...\) (bạn tự thay số bấm máy)
\(tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana.tanb}=...\)
\(cot\left(a+b\right)=\dfrac{1}{tan\left(a+b\right)}=\dfrac{1-tana.tanb}{tana+tanb}=...\)
e.
\(0< y< \dfrac{\pi}{2}\Rightarrow cosy>0\Rightarrow cosy=\sqrt{1-sin^2y}=\dfrac{4}{5}\)
\(\Rightarrow tany=\dfrac{siny}{cosy}=\dfrac{3}{4}\)
Vậy: \(tan\left(x+y\right)=\dfrac{tanx+tany}{1-tanx.tany}=...\)
\(cot\left(x-y\right)=\dfrac{1}{tan\left(x-y\right)}=\dfrac{1+tanx.tany}{tanx-tany}=...\)
Đúng 0
Bình luận (0)
Giúp e câu c vs d với ạ
Giúp em với ạ câu C,D,E
c) 108(12 + 13 ) + 25 . 92
= 2700 + 2300
= 5000
d) 2.169.12 - 3.68.8 - 24
= ( 2 .12 ) . 169 - (3.8) . 68 - 24
= 24 . 169 - 24 . 68 - 24
= 24(169 - 68 ) - 24
= 2424 - 24 = 2400
e) 2.56.24 - 3.36.16 + 4.12.95 + 6.3.8.5
= ( 2 . 24 ) . 56 - ( 3.16 ) . 36 + (4.12) .95 + (6.8) . 3 . 5
= 48 . 56 - 48 . 36 + 48 . 95 + 48 . 15
= 48(56 - 36 + 95 + 15 )
= 6240
Đúng 0
Bình luận (0)
c) 108.12+25.92+13.108
=(108+12)+(25.13)+(108+92)
=120+325+200
=645
Đúng 0
Bình luận (0)
























