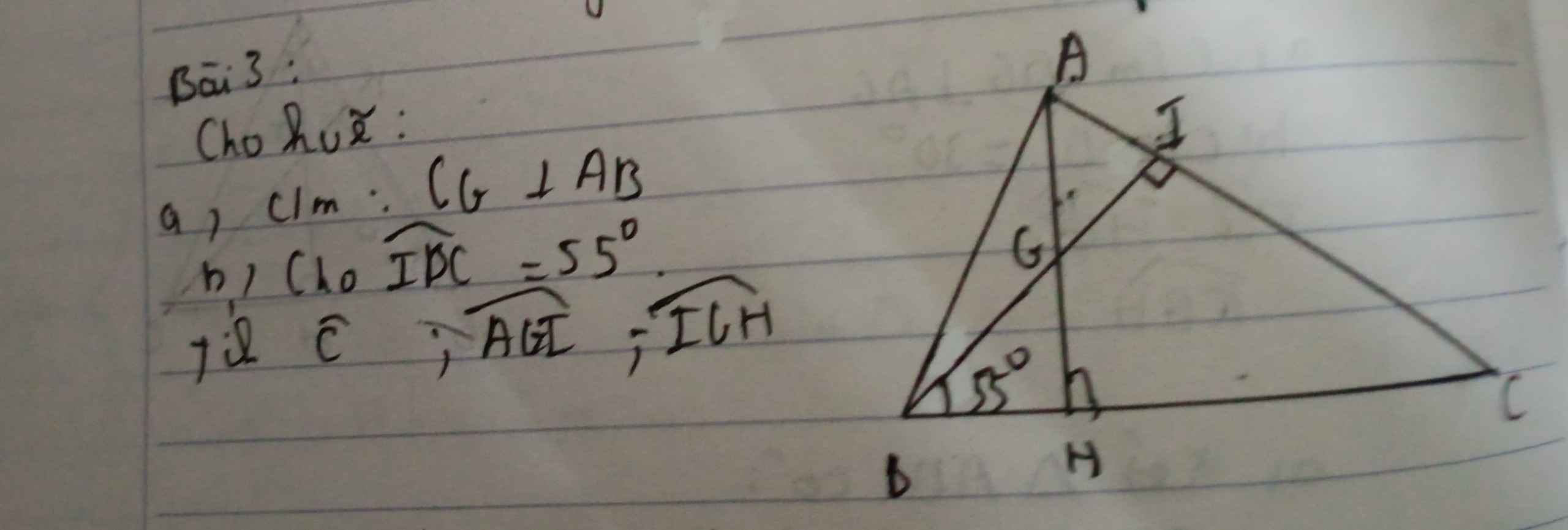
giúp mình câu b thôi ạ!!
Giúp mình câu b thôi ạ! Mình cảm ơn ạ!
b) Để P nguyên thì \(\sqrt{x}+5⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}+15⋮3\sqrt{x}-1\)
\(\Leftrightarrow16⋮3\sqrt{x}-1\)
\(\Leftrightarrow3\sqrt{x}-1\in\left\{-1;1;2;4;8;16\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;2;3;5;9;17\right\}\)
\(\Leftrightarrow3\sqrt{x}\in\left\{0;3;9\right\}\)
\(\Leftrightarrow\sqrt{x}\in\left\{0;1;3\right\}\)
hay \(x\in\left\{0;1;9\right\}\)
Giúp mình câu b thôi ạ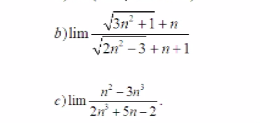
\(\lim\dfrac{\sqrt{3n^2+1}+n}{\sqrt{2n^2-3}+n+1}=\lim\dfrac{n\sqrt{3+\dfrac{1}{n^2}}+n}{n\sqrt{2-\dfrac{3}{n^2}}+n+1}\)
\(=\lim\dfrac{n\left(\sqrt{3+\dfrac{1}{n^2}}+1\right)}{n\left(\sqrt{2-\dfrac{3}{n^2}}+1+\dfrac{1}{n}\right)}=\lim\dfrac{\sqrt{3+\dfrac{1}{n^2}}+1}{\sqrt{2-\dfrac{3}{n^2}}+1+\dfrac{1}{n}}=\dfrac{\sqrt{3}+1}{\sqrt{2}+1}\)

*GIÚP MÌNH CÂU B THÔI Ạ!!!
Giúp mình câu b thôi ạ ^^
b: BC=2*5=10cm
FC=3/5AF
=>AF/FC=5/3
=>AF/AC=5/8
EF//BC
=>EF/BC=AF/AC
=>EF/10=5/8
=>EF=50/8=25/4cm

Giúp mình với, mai mình nộp rồi, mình cần câu b+c thôi ạ.
Giúp mình câu a, b bài 3 thôi ạ.
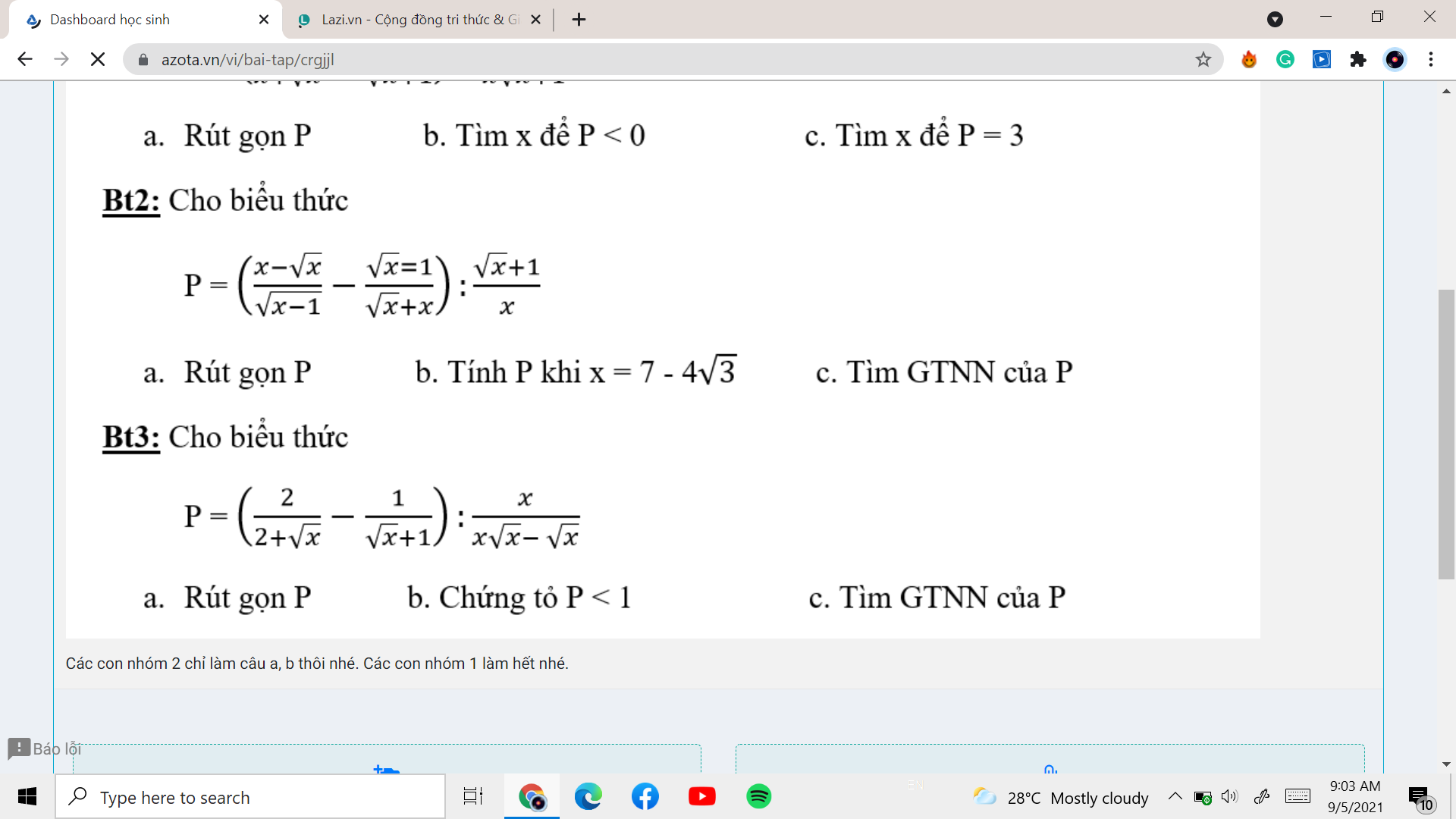
Bài 3:
a: Ta có: \(P=\left(\dfrac{2}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{x}{x\sqrt{x}-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}+2-\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{x}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
3.
b, ĐK: \(x>0;x\ne1\)
\(P< 1\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+2}< 1\)
\(\Leftrightarrow\sqrt{x}-1< \sqrt{x}+2\)
\(\Leftrightarrow3>0\)
\(\Rightarrow P< 1\forall x>0;x\ne1\)

làm nhanh giúp mình câu b và c thôi ạ
Giúp mình câu b và c thôi ạ. Mình cảm ơn Cho Tam giác nhọn ABC (AB
Giúp mình câu c với ạ, chỉ cần câu c thôi ạ!

Vì \(\widehat{MIA}=90^0\left(\text{góc nt chắn nửa đường tròn}\right)\) nên \(MI\perp IA\)
Xét \(\Delta MBP\) có \(\left\{{}\begin{matrix}PK\perp MB\left(PK\perp MN\right)\\MI\perp PB\left(MI\perp IA\right)\\\left\{H\right\}=PK\cap MI\end{matrix}\right.\) nên H là trực tâm
Do đó \(HB\perp PM\)
Mà \(AM\perp PM\Rightarrow HB\text{//}AM\)
Vì \(HB\text{//}OA\Rightarrow\dfrac{PB}{PA}=\dfrac{HB}{OA}\)
Ta có \(\sin MPB=\sin MPA=\dfrac{MA}{PA}=\dfrac{2OA}{PA}\)
\(\Rightarrow\dfrac{1}{2}BP\cdot\sin MPB=\dfrac{PB\cdot\dfrac{2OA}{PA}}{2}=\dfrac{PB\cdot2OA}{2PA}=\dfrac{PB}{PA}\cdot OA=\dfrac{HB}{OA}\cdot OA=HB\left(đpcm\right)\)