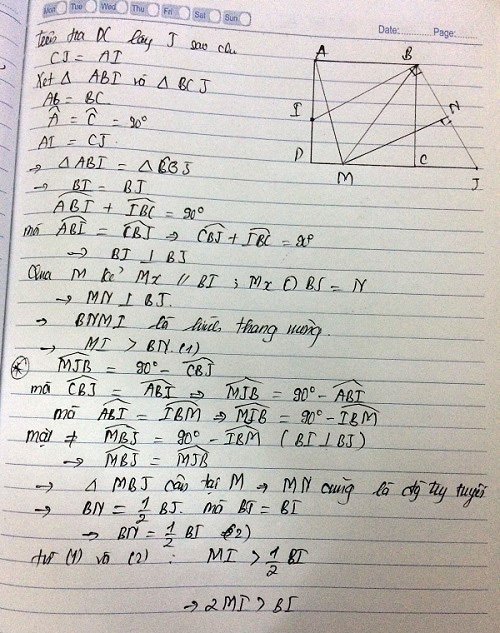Trên tia đối của tia CD em lấy điểm J sao cho CJ = AI. Qua M vẽ đường thẳng song song với BI cắt BJ tại N 
Dễ cm tam giác vuông ABI = tam giác vuông CBJ => BI = BJ 
Mặt khác dễ cm BI _|_ BJ => MN _|_ BJ 
Và => MBJ = 90⁰ - MBI => 90⁰ - ABI = 90⁰- CBJ = MJB => tam giác MBJ cân tại M => N là trung điểm của BJ 
Ta có MI >= BN = BJ/2 = BI/2 ( vì BIMN là hình thang vuông tại B và N) ( đpcm) 
Hay BI =< 2MI (đpcm)

a: Xét ΔABM vuông tại B và ΔADN vuông tại D có

AB=AD

BM=DN

Do đó: ΔABM=ΔADN

b: ΔABM=ΔADN

=>AM=AN và \(\widehat{MAB}=\widehat{NAD}\)

\(\widehat{MAB}+\widehat{DAM}=\widehat{BAD}=90^0\)

mà \(\widehat{MAB}=\widehat{NAD}\)

nên \(\widehat{DAM}+\widehat{DAN}=90^0\)

=>\(\widehat{MAN}=90^0\)

Xét ΔAMN có AM=AN và \(\widehat{MAN}=90^0\)

nênΔAMN vuông cân tại A

d: ΔAMN cân tại A

mà AI là đường phân giác

nên I là trung điểm của MN và AI\(\perp\)MN tại I

=>AP\(\perp\)MN tại I

Xét ΔPNM có

PI là đường cao

PI là đường trung tuyến

Do đó: ΔPNM cân tại P

=>PN=PM

=>PM=PD+DN=PD+BM

ST

tham khảo

Trên tia đối tia CD lấy điểm M sao cho CM = AK

Ta có: AK + CE = CM + CE = EM (*)

Xét ∆ ABK và ∆ CBM:

AB = CB (gt)

ˆA=ˆC=900

AK = CM (theo cách vẽ)

Do đó: ∆ ABK = ∆ CBM (c.g.c)

⇒ˆB1=ˆB4

(1)

ˆKBC=900–ˆB1

(2)

Trong tam giác CBM vuông tại C.

ˆM=900–ˆB4

(3)

Từ (1), (2) và (3) suy ra: ˆKBC=ˆM

(4)

ˆKBC=ˆB2+ˆB3

 mà  ˆB1=ˆB2

(gt)

ˆB1=ˆB4

(chứng minh trên)

Suy ra: ˆB2=ˆB4⇒ˆB2+ˆB3=ˆB3+ˆB4

hay ˆKBC=ˆEBM

(5)

Từ (4) và (5) suy ra: ˆEBM=ˆM

⇒ ∆ EBM cân tại E ⇒ EM = BE (**)

Từ (*) và (**) suy ra: AK + CE = BE

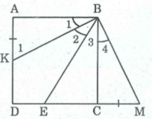
Trên tia đối của tia CD lấy điểm M sao cho CM = AK

Ta có: AK + CE = CM + CE = EM (1)

Xét ∆ ABK và  ∆ CBM, ta có:

AB = CB (gt)

∠ A = ∠ C = 90 0

AK = CM (theo cách vẽ)

Suy ra:  ∆ ABK = ∆ CBM (c.g.c)

⇒  ∠ B 1  =  ∠ B 4  (2)

Lại có:  ∠ B 1 = ∠ B 2  ( do BK là tia phân giác của ABE)

Suy ra:  ∠ B 1  =  ∠ B 2  =  ∠ B 4

Mà  ∠ (KBC) =  90 0  -  ∠ B 1  (3)

Tam giác CBM vuông tại C nên:  ∠ M =  90 0  -  ∠ B 4  (4)

Từ (2), (3) và (4) suy ra:  ∠ (KBC) =  ∠ M (5)

Hay  ∠ B 2 +  ∠ B 3  =  ∠ M

⇒  ∠ B 4  +  ∠ B 3  =  ∠ M( vì  ∠ B 2  =  ∠ B 4  )

Hay:  ∠ (EBM) =  ∠ M

⇒  ∆ EBM cân tại E ⇒ EM = BE. (6)

Từ (1) và (6) suy ra: AK + CE = BE.