a: Xét tứ giác AEHF có \(\hat{AEH}+\hat{AFH}=90^0+90^0=180^0\)

nên AEHF là tứ giác nội tiếp

b: AEHF là tứ giác nội tiếp

=>\(\hat{FAH}=\hat{FEH}\)

=>\(\hat{FAD}=\hat{FEB}\) (1)

Xét tứ giác BFEC có \(\hat{BFC}=\hat{BEC}=90^0\)

nên BFEC là tứ giác nội tiếp đường tròn đường kính BC

=>BFEC nội tiếp (O)

=>OB=OC=OE=OF

BFEC nội tiếp

=>\(\hat{FEB}=\hat{FCB}\)

=>\(\hat{FEB}=\hat{OCF}\)

mà \(\hat{OCF}=\hat{OFC}\) (ΔOFC cân tại O)

nên \(\hat{FEB}=\hat{OFC}\) (2)

Từ (1),(2) suy ra \(\hat{OFC}=\hat{FAD}\)

BFEC là tứ giác nội tiếp

=>\(\hat{FEC}+\hat{FBC}=180^0\)

mà \(\hat{FEC}+\hat{AEF}=180^0\) (hai góc kề bù)

nên \(\hat{AEF}=\hat{ABC}\)

ΔOEC có OE=OC

nên ΔOCE cân tại O

=>\(\hat{OEC}=\hat{OCE}=\hat{ACB}\)

\(\hat{AEF}+\hat{FEO}+\hat{OEC}=180^0\)

=>\(\hat{ABC}+\hat{OEF}+\hat{ACB}=180^0\)

=>\(\hat{OEF}=180^0-\left(\hat{ABC}+\hat{ACB}\right)=\hat{BAC}\)

Xét tứ giác AFDC có \(\hat{AFC}=\hat{ADC}=90^0\)

nên AFDC là tứ giác nội tiếp

=>\(\hat{FDC}+\hat{FAC}=180^0\)

=>\(\hat{FDO}+\hat{BAC}=180^0\)

=>\(\hat{FDO}+\hat{FEO}=180^0\)

=>FEOD là tứ giác nội tiếp

=>\(\hat{ODE}=\hat{OFE}\)

mà \(\hat{OFE}=\hat{OEF}\) (ΔOEF cân tại O)

nên \(\hat{ODE}=\hat{OEF}\)

=>\(\hat{ODE}=\hat{OEM}\)

Xét ΔODE và ΔOEM có

\(\hat{ODE}=\hat{OEM}\)

góc DOE chung

Do đó: ΔODE~ΔOEM

=>\(\frac{OD}{OE}=\frac{OE}{OM}\)

=>\(OD\cdot OM=OE^2\)

=>\(OD\cdot OM=OC^2\)

`bb5)`

`x/3 - ( 2x + 1 )/6 = x/6 - x`

`<=> ( 2x )/6 - ( 2x+1 )/6 = x/6 - ( 6x )/6`

`=> 2x-( 2x+1) = x - 6x`

`<=> 2x-2x-1=-5x`

`<=> -1=-5x`

`<=> 1=5x`

`<=> x = 1/5``(tm)`

Vậy `S={1/5}` 

`5)x/3-[2x+1]/6=x/6-x`

`<=>[2x-2x-1]/6=[x-6x]/6`

`<=>2x-2x-1=x-6x`

`<=>2x-2x-x+6x=1`

`<=>5x=1`

`<=>x=1/5`

Vậy `S={1/5}`

____________________________________

`6)[x+1]/2004+[x+2]/2003=[x+3]/2002+[x+4]/2001`

`<=>[x+1]/2004+1+[x+2]/2003+1=[x+3]/2002+1+[x+4]/2001+1`

`<=>[x+1+2004]/2004+[x+2+2003]/2003-[x+3+2002]/2002-[x+4+2001]/2001=0`

`<=>[x+2005]/2004+[x+2005]/2003-[x+2005]/2002-[x+2005]/2001=0`

`<=>(x+2005)(1/2004+1/2003-1/2002-1/2001)=0`

     Mà `1/2004+1/2003-1/2002-1/2001 \ne 0`

  `=>x+2005=0`

`<=>x=-2005`

Vậy `S={-2005}`

\(\dfrac{x}{3}-\dfrac{2x+1}{6}=\dfrac{x}{6}-x\)

\(\Leftrightarrow\dfrac{2x-\left(2x+1\right)}{6}=\dfrac{x-6x}{6}\)

\(\Leftrightarrow2x-2x-1=x-6x\)

\(\Leftrightarrow-5x=-1\)

\(\Leftrightarrow x=\dfrac{1}{5}\)

Vậy \(S=\left\{\dfrac{1}{5}\right\}\)

\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)

6a.

$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$

$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$

Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$

a: Xét tứ giác OAIC có \(\hat{OAI}+\hat{OCI}=90^0+90^0=180^0\)

nên OAIC là tứ giác nội tiếp

b: Xét (O) có

ΔCDB nội tiếp

CB là đường kính

Do đó: ΔCDB vuông tại D

=>CD⊥IB tại D

Xét ΔICB vuông tại C có CD là đường cao

nên \(ID\cdot IB=IC^2\)

c: ΔOBD cân tại O

mà OM là đường trung tuyến

nên OM⊥BD tại M

Xét tứ giác OMIC có \(\hat{OMI}+\hat{OCI}=90^0+90^0=180^0\)

nên OMIC là tứ giác nội tiếp

=>\(\hat{CMI}=\hat{COI}\)

mà \(\hat{COI}=\hat{CAI}\) (OAIC nội tiếp)

nên \(\hat{CMI}=\hat{CAI}\) (1)

Xét (O) có

\(\hat{CAI}\) là góc tạo bởi tiếp tuyến AI và dây cung AC

\(\hat{AEC}\) là góc nội tiếp chắn cung AC

Do đó: \(\hat{CAI}=\hat{AEC}\) (2)

Từ (1),(2) suy ra \(\hat{CMI}=\hat{CEA}\)

mà hai góc này là hai góc ở vị trí đồng vị

nne IM//AE

Ta có: OM⊥IM

IM//AE

Do đó: OM⊥AE

mn ơi mình cần gấp ạ

1 you are => are you

2 fiveteen => fifteen

3 are => is

4 am => are

5 is => bỏ

6 thanks => thank

7 year => years

8 are => is

9 phong is => is phong

10 is => are

Câu 3 bài đầu là IS THIS PHONG ?

Bài 3 câu 3 là My name is Linh

Chúc bn học tốt nè

\(a,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{x-2}=x-2\\ \Leftrightarrow x-2=x^2-4x+4\\ \Leftrightarrow x^2-5x+6=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=3\left(tm\right)\end{matrix}\right.\\ b,ĐK:x\ge5\\ PT\Leftrightarrow x^2-2x+3=x^2-10x+25\\ \Leftrightarrow8x=22\Leftrightarrow x=\dfrac{11}{4}\left(ktm\right)\\ \Leftrightarrow x\in\varnothing\\ c,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow9\left(2x-1\right)=\left(2x-5\right)^2\\ \Leftrightarrow18x-9=4x^2-20x+25\\ \Leftrightarrow4x^2-38x+24=0\\ \Leftrightarrow2x^2-19x+12=0\\ \Delta=361-96=265\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{19-\sqrt{265}}{4}\left(tm\right)\\x=\dfrac{19+\sqrt{265}}{4}\left(tm\right)\end{matrix}\right.\)

\(d,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{\left(\sqrt{x-2}+1\right)^2}=\sqrt{x-2}+1\\ \Leftrightarrow\sqrt{x-2}+1-\sqrt{x-2}-1=0\\ \Leftrightarrow0=0\left(luôn.đúng\right)\Leftrightarrow x\in R;x\ge2\)

\(e,ĐK:x\ge3\\ PT\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=2\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=3\\ f,ĐK:x\ge1\\ PT\Leftrightarrow3\sqrt{x-1}-2\sqrt{x-1}+4\sqrt{x-1}-3\sqrt{x-1}=16\\ \Leftrightarrow\sqrt{x-1}=8\\ \Leftrightarrow x-1=64\Leftrightarrow x=65\left(tm\right)\)

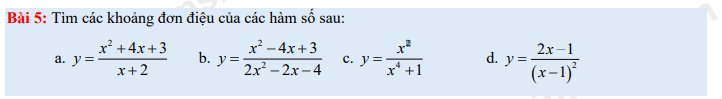
b: ĐKXĐ: \(2x^2-2x-4<>0\)

=>\(x^2-x-2<>0\)

=>(x-2)(x+1)<>0

=>x∉{2;-1}

Ta có: \(y=\frac{x^2-4x+3}{2x^2-2x-4}\)

=>\(y^{\prime}=\frac{\left(x^2-4x+3\right)^{\prime}\left(2x^2-2x-4\right)-\left(x^2-4x+3\right)\left(2x^2-2x-4\right)^{\prime}}{\left(2x^2-2x-4\right)^2}\)

=>\(y^{\prime}=\frac{\left(2x-4\right)\left(2x^2-2x-4\right)-\left(x^2-4x+3\right)\left(4x-2\right)}{\left(2x^2-2x-4\right)^2}\)

=>\(y^{\prime}=\frac{4x^3-4x^2-8x-8x^2+8x+16-\left(4x^3-2x^2-16x^2+8x+12x-6\right)}{\left(2x^2-2x-4\right)^2}\)

=>\(y^{\prime}=\frac{4x^3-12x^2+16-\left(4x^3-18x^2+20x-6\right)}{\left(2x^2-2x-4\right)^2}=\frac{6x^2-20x+22}{\left(2x^2-2x-4\right)^2}\)

Đặt y'>0

=>\(6x^2-20x+22>0\)

=>\(3x^2-10x+11>0\)

=>\(x^2-\frac{10}{3}x+\frac{11}{3}>0\)

=>\(x^2-\frac{10}{3}x+\frac{25}{9}+\frac{11}{3}-\frac{25}{9}>0\)

=>\(\left(x-\frac53\right)^2+\frac89>0\) (luôn đúng)

=>Hàm số đồng biến trên các khoảng xác định của nó

=>Hàm số đồng biến trên các khoảng (-∞;-1); (-1;2); (2;+∞)

d: \(y=\frac{2x-1}{\left(x-1\right)^2}\) (ĐKXĐ: x<>1)

=>\(y=\frac{2x-1}{x^2-2x+1}\)

=>\(y^{\prime}=\frac{\left(2x-1\right)^{\prime}\left(x^2-2x+1\right)-\left(2x-1\right)\left(x^2-2x+1\right)^{\prime}}{\left(x^2-2x+1\right)^2}\)

=>\(y^{\prime}=\frac{2\left(x^2-2x+1\right)-\left(2x-1\right)\left(2x-2\right)}{\left(x^2-2x+1\right)^2}=\frac{2x^2-4x+2-\left(4x^2-6x+2\right)}{\left(x^2-2x+1\right)^2}\)

\(=\frac{2x^2-4x+2-4x^2+6x-2}{\left(x^2-2x+1\right)^2}=\frac{-2x^2+2x}{\left(x^2-2x+1\right)^2}=\frac{-2x\left(x-1\right)}{\left(x^2-2x+1\right)^2}\)

Đặt y'<0

=>-2x(x-1)<0

=>x(x-1)>0

=>\(\left[\begin{array}{l}x>1\\ x<0\end{array}\right.\)

=>Hàm số nghịch biến trên các khoảng (1;+∞) và (-∞;0)

Đặt y'>0

=>-2x(x-1)>0

=>x(x-1)<0

=>0<x<1

=>Hàm số đồng biến trên khoảng (0;1)