`bb5)`
`x/3 - ( 2x + 1 )/6 = x/6 - x`
`<=> ( 2x )/6 - ( 2x+1 )/6 = x/6 - ( 6x )/6`
`=> 2x-( 2x+1) = x - 6x`
`<=> 2x-2x-1=-5x`
`<=> -1=-5x`
`<=> 1=5x`
`<=> x = 1/5``(tm)`
Vậy `S={1/5}`
`5)x/3-[2x+1]/6=x/6-x`
`<=>[2x-2x-1]/6=[x-6x]/6`
`<=>2x-2x-1=x-6x`
`<=>2x-2x-x+6x=1`
`<=>5x=1`
`<=>x=1/5`
Vậy `S={1/5}`
____________________________________
`6)[x+1]/2004+[x+2]/2003=[x+3]/2002+[x+4]/2001`
`<=>[x+1]/2004+1+[x+2]/2003+1=[x+3]/2002+1+[x+4]/2001+1`
`<=>[x+1+2004]/2004+[x+2+2003]/2003-[x+3+2002]/2002-[x+4+2001]/2001=0`
`<=>[x+2005]/2004+[x+2005]/2003-[x+2005]/2002-[x+2005]/2001=0`
`<=>(x+2005)(1/2004+1/2003-1/2002-1/2001)=0`
Mà `1/2004+1/2003-1/2002-1/2001 \ne 0`
`=>x+2005=0`
`<=>x=-2005`
Vậy `S={-2005}`
\(\dfrac{x}{3}-\dfrac{2x+1}{6}=\dfrac{x}{6}-x\)
\(\Leftrightarrow\dfrac{2x-\left(2x+1\right)}{6}=\dfrac{x-6x}{6}\)
\(\Leftrightarrow2x-2x-1=x-6x\)
\(\Leftrightarrow-5x=-1\)
\(\Leftrightarrow x=\dfrac{1}{5}\)
Vậy \(S=\left\{\dfrac{1}{5}\right\}\)
`bb6)`
`( x + 1 )/2004 + ( x +2 )/2003 = ( x +3)/2002+(x+4)/2001`
`<=> ( x + 1 )/2004+1+ ( x +2 )/2003+1 = ( x +3)/2002+1+(x+4)/2001+1`
`<=> ( x + 2005 )/2004+ ( x +2005 )/2003 = ( x +2005)/2002+(x+2005)/2001`
`<=> ( x + 2005 )/2004+ ( x +2005 )/2003 - [( x +2005)/2002+(x+2005)/2001]=0`
`<=> ( x+2005)(1/2004+1/2003-1/2002-1/2001)=0`
Do `1/2004+1/2003-1/2002-1/2001 \ne 0`
`=>x+2005=0`
`<=> x=-2005`
Vậy `S={-2005}`
















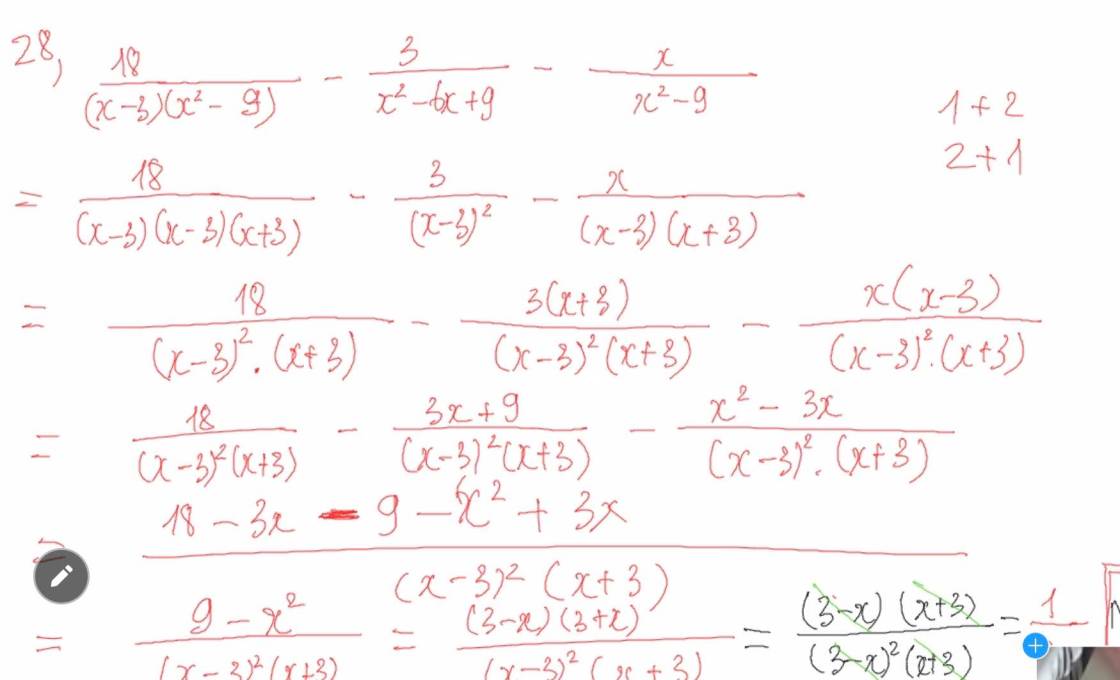
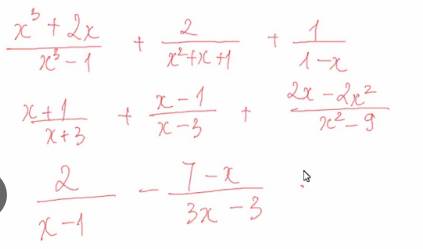

 giúp mình với ạ, mình cần gấp lắm ạ
giúp mình với ạ, mình cần gấp lắm ạ





