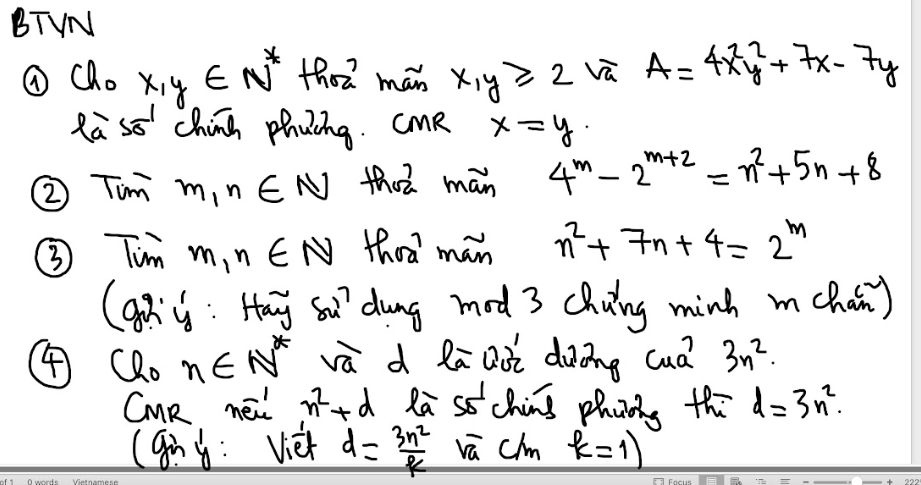a: \(A=\dfrac{2x^2+x^2-1-2x^2+2x+1}{x\left(x+1\right)}=\dfrac{x^2+2x}{x\left(x+1\right)}=\dfrac{x+2}{x+1}\)
b: Ta có: \(x^2-2x=0\)
=>x=2
Thay x=2 vào A, ta được:
\(A=\dfrac{2+2}{2+1}=\dfrac{4}{3}\)
(a)
\(A=\dfrac{2x}{x+1}+\dfrac{x-1}{x}-\dfrac{2x^2-2x-1}{x^2+x}\\ =\dfrac{2x}{x+1}+\dfrac{x-1}{x}-\dfrac{2x^2-2x-1}{x\left(x+1\right)}=\dfrac{2x^2}{x\left(x+1\right)}+\dfrac{x^2-1}{x\left(x+1\right)}-\dfrac{2x^2-2x-1}{x\left(x-1\right)}\)
\(=\dfrac{2x^2+x^2-1-2x^2+2x+1}{x\left(x+1\right)}=\dfrac{x^2+2x+1}{x\left(x+1\right)}=\dfrac{\left(x+1\right)\left(x+1\right)}{x\left(x+1\right)}=\dfrac{x+1}{x}\)
(b)
\(x^2-2x=0\\ x\left(x-2\right)=0\)
=>x=0 hoặc x=2 mà đk x khác 0 nên thay x=2 vào bt A , ta có:
\(\dfrac{x+1}{x}=\dfrac{2+1}{2}=\dfrac{3}{2}\)