- Đây có phải là toán lớp 8 nữa không vậy :)? Mình học toán nâng cao nhưng chưa bao giờ thấy dạng này :).
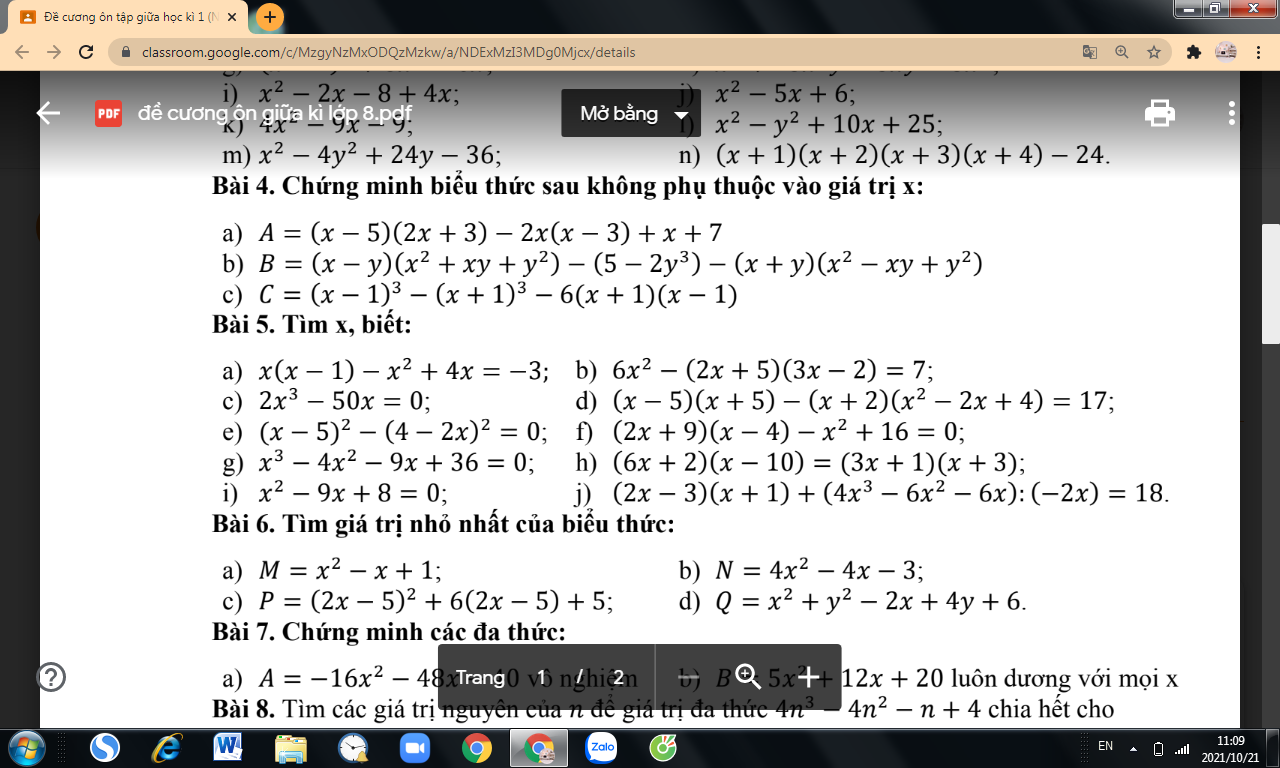
b1:
do x;y thuộc số nguyên N và x,y\(\ge\)2
=>\(-4xy+1< +7x-7y< 4xy+1\)
\(\Rightarrow4x^2y^2-4xy+1< 4x^2y^2+7x-7y< 4x^2y^2+4xy+1\)
\(\Rightarrow\left(2xy-1\right)^2< 4x^2y^2+7x-7y< \left(2xy+1\right)^2\)
mà \(4x^2y^2+7x-7y\) là số chính phương và 1<2xy-1<2xy-1 nên ta có:
\(4x^2y^2+7x-7y-\left(2xy\right)^2\Leftrightarrow x=y\)
1.
TH1: \(x>0\Rightarrow7\left(x-y\right)>0\Rightarrow A>4x^2y^2\)
\(4xy-7x+7y+1>4xy-8x+7y+1=4x\left(y-2\right)+7y+1>0\) do \(x;y\ge2\)
\(\Rightarrow4xy+1>7x-7y\Rightarrow A< 4x^2y^2+4xy+1\)
\(\Rightarrow\left(2xy\right)^2< A< \left(2xy+1\right)^2\)
\(\Rightarrow A\) nằm giữa 2 SCP liên tiếp nên ko thể là SCP
TH2: \(x< y\) , tương tự ta có: \(7\left(x-y\right)< 0\Rightarrow A< 4x^2y^2\)
\(4xy+7x-7y-1>4xy+7x-8y-1=4y\left(x-2\right)+\left(7x-1\right)>0\)
\(\Rightarrow7x-7y>-4xy+1\Rightarrow A>4x^2y^2-4xy+1\)
\(\Rightarrow\left(2xy-1\right)^2< A< \left(2xy\right)^2\)
\(\Rightarrow A\) ko thể là SCP
TH3: \(x=y\Rightarrow A=\left(2xy\right)^2\) là SCP (thỏa mãn)
Vậy \(x=y\)
2.
\(\Leftrightarrow4^m-4.2^m+1=n^2+5n+9\)
\(\Leftrightarrow\left(2^m-1\right)^2=n^2+6n+9-n\)
\(\Leftrightarrow n=\left(n+3\right)^2-\left(2^m-1\right)^2\)
\(\Leftrightarrow n=\left(n+2+2^n\right)\left(n+4-2^m\right)\)
TH1: \(n+4-2^m=0\Rightarrow n=0\Rightarrow m=2\)
TH2: \(n+4-2^m⋮0\Rightarrow\left\{{}\begin{matrix}n\ne0\\n⋮\left(n+2+2^m\right)\end{matrix}\right.\)
\(\Rightarrow n\ge n+2+2^m\) (vô lý)
3.
\(\Leftrightarrow\left(n+3\right)\left(n+4\right)-9+1=2^m\)
Do tích 2 số tự nhiên liên tiếp chia 3 chỉ có thể dư 0 hoặc 2
\(\Rightarrow\) Vế trái chia 3 luôn dư 0 hoặc 1
\(\Rightarrow2^m\) chia 3 dư 1
\(\Rightarrow m\) chẵn \(\Rightarrow m=2k\)
\(\Rightarrow n^2+7n+4=2^{2k}\)
\(\Leftrightarrow4n^2+28n+16=4.2^{2k}\)
\(\Leftrightarrow\left(2n+7\right)^2-33=\left(2.2^k\right)^2\)
\(\Leftrightarrow\left(2n+7-2.2^k\right)\left(2n+7+2.2^k\right)=33\)
Phương trình ước số cơ bản, em tự giải
4.
Do d là ước dương của \(3n^2\Rightarrow3n^2=d.k\Rightarrow d=\dfrac{3n^2}{k}\)
Theo giả thiết:
\(n^2+d=a^2\Leftrightarrow n^2+\dfrac{3n^2}{k}=a^2\)
\(\Leftrightarrow k.n^2+3n^2=k.a^2\)
\(\Leftrightarrow k^2n^2+3n^2.k=k^2a^2\)
\(\Leftrightarrow n^2\left(k^2+3k\right)=\left(ak\right)^2\)
\(\Rightarrow k^2+3k\) cũng là SCP
Mặt khác:
\(k^2< k^2+3k< k^2+4k+4\)
\(\Rightarrow k^2< k^2+3k< \left(k+2\right)^2\)
\(\Rightarrow k^2+3k=\left(k+1\right)^2\)
\(\Rightarrow k=1\)
Vậy \(d=\dfrac{3n^2}{1}=3n^2\)

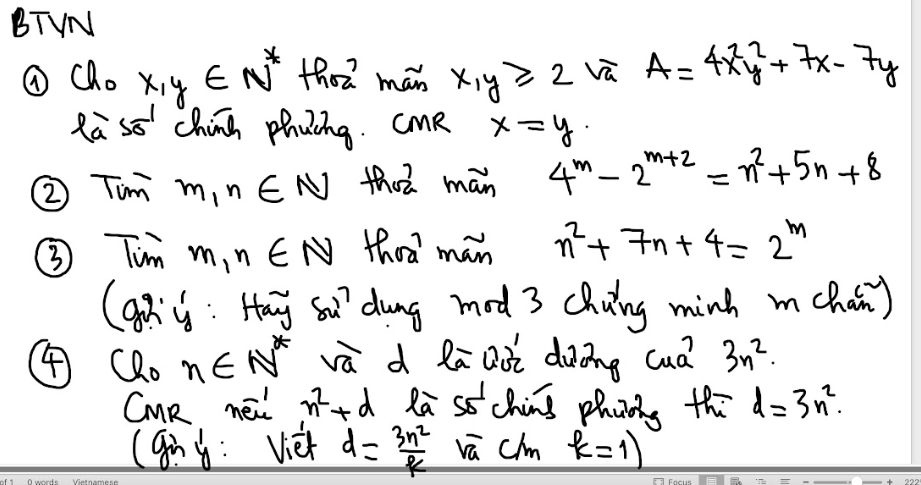











 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ