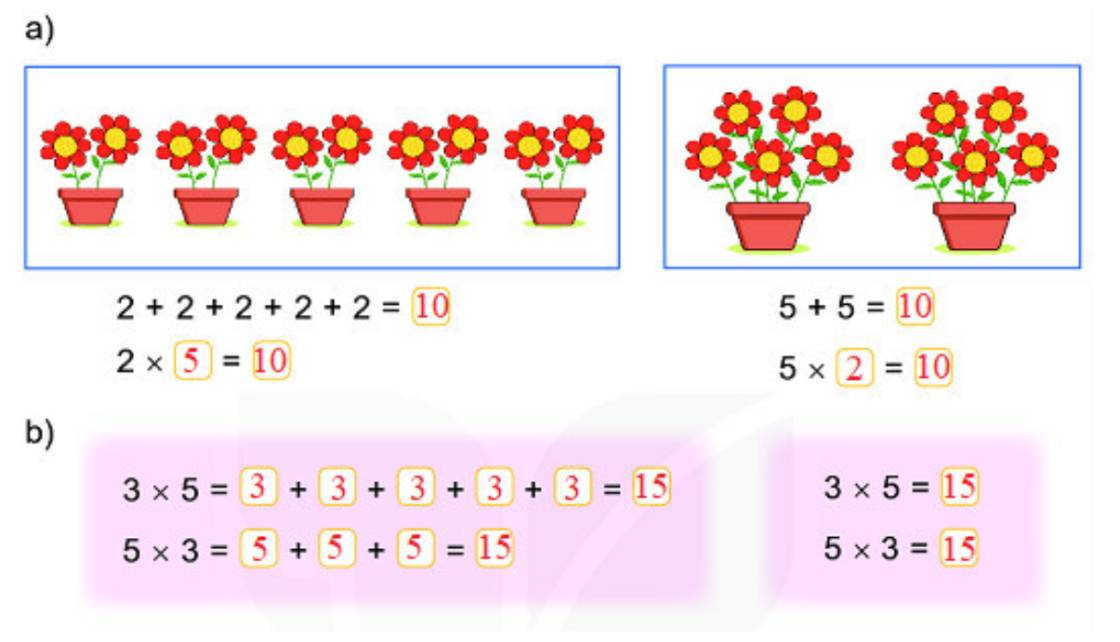
A=|x-5|+5
Những câu hỏi liên quan
Cho A(x)= ( x-5 )+ 2015
B(x)= 5-5 / x-5 /
a, Tính A(-5), A(5), B(-5), B(5)
b, Tính giá trị nhỏ nhất của Y(x)= A(x) - B(x)+ 5
A=5^0+5^2+5^4+...+5^x (x thuộc N;x lớn hơn hoặc bằng 2)
A=5^1+5^3+5^5+...+5^x (x thuộc N;x lớn hơn hoặc bằng 2)
A=5^1+5^3+5^5+...+5^x (x thuộc N;x lớn hơn hoặc bằng 2)
CẦN GẤP MAI NỘP RỒI
Cho biểu thức \(A=\dfrac{\sqrt{x}}{\sqrt{x}-5}-\dfrac{10\sqrt{x}}{x-25}-\dfrac{5}{\sqrt{x}+5}\)với \(x\ge0,x\ne25\)
Biểu thức A sau khi rút gọn là A = \(\dfrac{\sqrt{x}-5}{\sqrt{x}+5}\)
1) So sánh A với 2
Có \(A=\dfrac{\sqrt{x}-5}{\sqrt{x}+5}=1-\dfrac{10}{\sqrt{x}+5}\)
Dễ thấy \(\dfrac{10}{\sqrt{x}+5}>0\forall x\Rightarrow A=1-\dfrac{10}{\sqrt{x}+5}< 1\)
=> A < 2
Đúng 2
Bình luận (0)
Điền số thích hợp vào chỗ chấm
a) 5 + 5 + 5 + 5 + 5 = 5 x …
b) 5 + 5 – 5 + 5 + 5 = 5 x …
c) 5 – 5 + 5 + 5 + 5 + 5 = 5 x …
d) 5 + 5 + 5 + 5 + 5 + 5 = 5 x …
a) 5 + 5 + 5 + 5 + 5 = 5 x 5
b) 5 + 5 – 5 + 5 + 5 = 5 x 3
c) 5 – 5 + 5 + 5 + 5 + 5 = 5 x 4
d) 5 + 5 + 5 + 5 + 5 + 5 = 5 x 6
Đúng 0
Bình luận (0)
SGK Kết nối tri thức với cuộc sống - Trang 5
14 tháng 4 2023 lúc 20:58
Số?a) 2 + 2 + 2 + 2 + 2 2 x 5 + 5 5 x b) 3 x 5 3 x 5 5 x 3 5 x 3
Đọc tiếp
Số?
a)
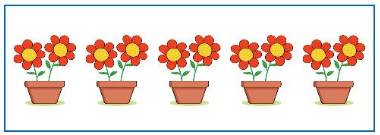
2 + 2 + 2 + 2 + 2 = 
2 x 
= 
5 + 5 = 
5 x 
= 
b)
3 x 5 = 
3 x 5 = 
5 x 3 = 
5 x 3 = 
a) \(2+2+2+2+2=2\times5=10\)
\(2\times5=10\)
\(5+5=2\times5=10\)
\(5\times2=10\)
b) \(3\times5=3+3+3+3+3=15\)
\(5\times3=5+5+5=15\)
\(3\times5=5+5+5=15\)
\(5\times3=3+3+3+3+3=15\)
Đúng 1
Bình luận (0)
a) 2 + 2 + 2 + 2 + 2 = 10
2 x 5 = 10
5 + 5 = 10
5 x 2 = 10
b) 3 x 5 = 3 + 3 + 3 + 3 + 3 = 15
5 x 3 = 5 + 5 + 5 = 15
3 x 5 = 15
5 x 3 = 15
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
2 tháng 12 2019 lúc 18:22
4 x A + 5 = 5x. Với A = 5 + 52 + 53 + ... + 5100
Tìm x ở kết quả : 5x
ào tôi giải ở đó rồi nha https://loga.vn/hoi-dap/5-chung-minh-phep-tinh-nay-chia-het-cho-6-20224
5(x-2)+x(x-2)=0 C. x=2 ; x=-5 D.x=-2 ; x=5 A. x=2 ; x=5 B.x=-2 ; x=-5
27 tháng 9 2023 lúc 20:59
Cho biểu thức A dfrac{sqrt{x}}{sqrt{x}-5}-dfrac{10sqrt{x}}{x-25}-dfrac{5}{sqrt{x}+5} với xge0,xne25.Biểu thức A sau khi rút gọn là: dfrac{sqrt{x}-5}{sqrt{x}+5}2) Tìm giá trị nhỏ nhất của A
Đọc tiếp
Cho biểu thức A = \(\dfrac{\sqrt{x}}{\sqrt{x}-5}-\dfrac{10\sqrt{x}}{x-25}-\dfrac{5}{\sqrt{x}+5}\) với \(x\ge0,x\ne25\).
Biểu thức A sau khi rút gọn là: \(\dfrac{\sqrt{x}-5}{\sqrt{x}+5}\)
2) Tìm giá trị nhỏ nhất của A
2: \(A=\dfrac{\sqrt{x}-5}{\sqrt{x}+5}=\dfrac{\sqrt{x}+5-10}{\sqrt{x}+5}\)
\(=1-\dfrac{10}{\sqrt{x}+5}\)
\(\sqrt{x}+5>=5\forall x\)
=>\(\dfrac{10}{\sqrt{x}+5}< =\dfrac{10}{5}=2\forall x\)
=>\(-\dfrac{10}{\sqrt{x}+5}>=-2\forall x\)
=>\(-\dfrac{10}{\sqrt{x}+5}+1>=-2+1=-1\forall x\)
Dấu '=' xảy ra khi x=0
Vậy: \(A_{min}=-1\) khi x=0
Đúng 1
Bình luận (0)
Rút gọn biểu thức sau:
a) A = \(\dfrac{x+\sqrt{5}}{x^2+2x\sqrt{5}+5}\), x ≠ \(-\sqrt{5}\)
b) B = \(\dfrac{a-2\sqrt{a}-3}{a-9}\), a ≥ 0, a ≠ 9
c) C = \(\sqrt{x-1-2\sqrt{x-2}}\)
a) Ta có: \(\dfrac{x+\sqrt{5}}{x^2+2x\sqrt{5}+5}\)
\(=\dfrac{x+\sqrt{5}}{\left(x+\sqrt{5}\right)^2}=\dfrac{1}{x+\sqrt{5}}\)
b) Ta có: \(B=\dfrac{a-2\sqrt{a}-3}{a-9}\)
\(=\dfrac{\left(\sqrt{a}-3\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-3\right)\left(\sqrt{a}+3\right)}\)
\(=\dfrac{\sqrt{a}+1}{\sqrt{a}+3}\)
c) Ta có: \(C=\sqrt{x-1-2\sqrt{x-2}}\)
\(=\sqrt{x-2-2\cdot\sqrt{x-2}\cdot1+1}\)
\(=\sqrt{\left(\sqrt{x-2}-1\right)^2}\)
\(=\left|\sqrt{x-2}-1\right|\)
Đúng 1
Bình luận (0)
`a)A=(x+sqrt5)(x^2+2xsqrt5+5)`
`=(x+sqrt5)/(x+sqrt5)^2=1/(x+sqrt5)`
`b)B=(a-2sqrta-3)/(a-9)(a>=0,a ne 9)`
`=(a+sqrta-3sqrta-3)/(a-9)`
`=((sqrta+1)(sqrta-3))/((sqrta-3)(sqrta+3))`
`=(sqrta+1)/(sqrta+3)`
`c)C=sqrt{x-1-2sqrt{x-2}}(x>=2)`
`=sqrt{x-2-2sqrt{x-2}+1}`
`=sqrt{(sqrt{x-2}-1)^2}`
`=|sqrt(x-2)-1|`
Đúng 1
Bình luận (0)
Tìm x :
a)4/5 : x = 5/7
b)5/6 - 3/5 : x = 2/5
a) x = 4/5 : 5/7
x = 28/25
b) 3/5 : x = 5/6 - 2/5
3/5 : x = 13/30
x = 3/5 : 13/30
x = 18/13
Đúng 2
Bình luận (0)
\(a,\Leftrightarrow x=\dfrac{4}{5}:\dfrac{5}{7}\)
\(\Leftrightarrow x=\dfrac{28}{25}\)
\(b,\Leftrightarrow\dfrac{3}{5}:x=\dfrac{13}{30}\)
\(\Leftrightarrow x=\dfrac{18}{13}\)
Đúng 2
Bình luận (0)
a)\(=>x=\dfrac{4}{5}\times\dfrac{7}{5}=\dfrac{28}{25}\)
b)\(=>x=\dfrac{3}{5}:\left(\dfrac{5}{6}-\dfrac{2}{5}\right)=\dfrac{3}{5}:\dfrac{13}{30}=\dfrac{18}{13}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời