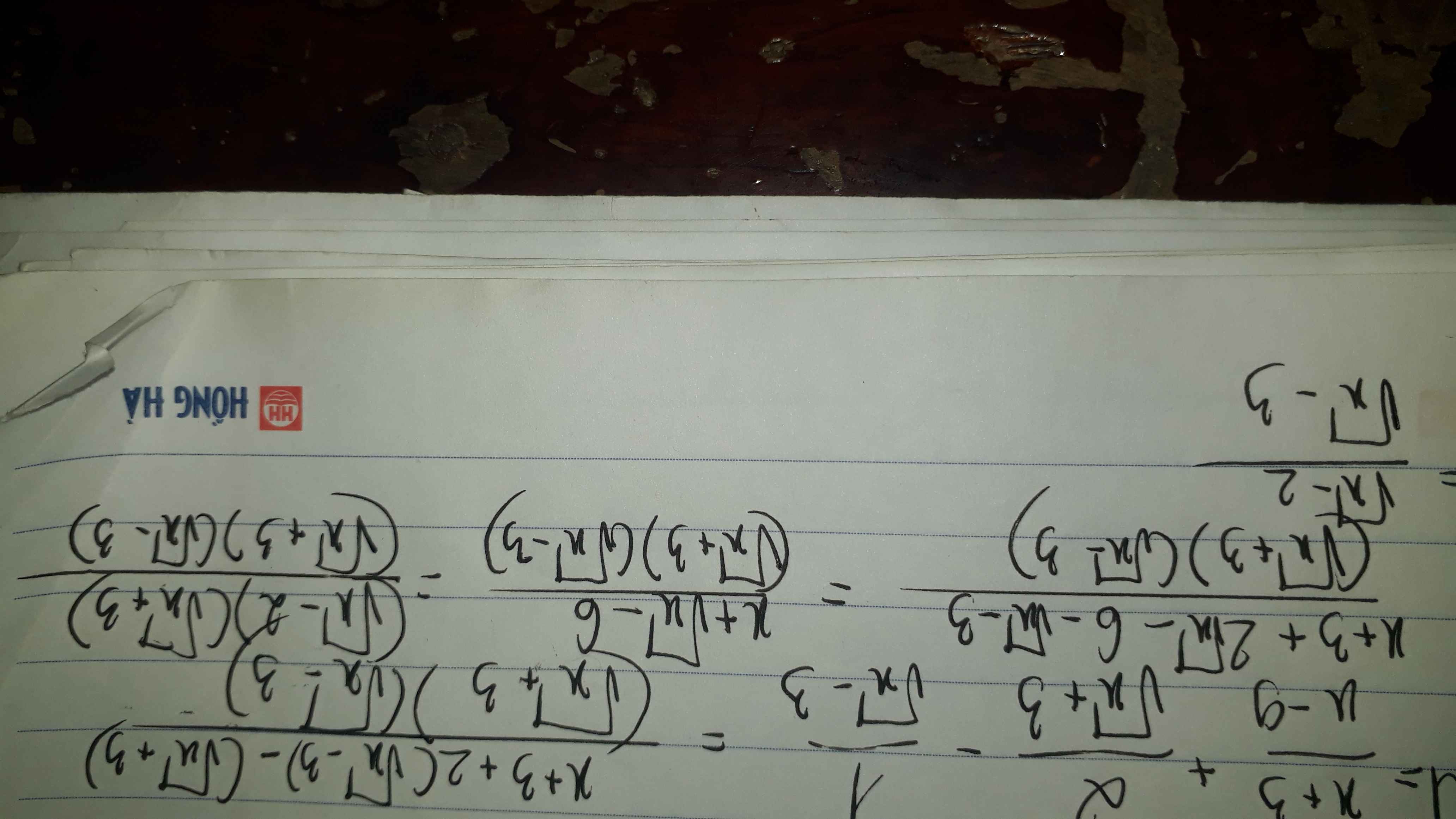rút gọn \(\dfrac{x+3}{9-x^2}\)

Những câu hỏi liên quan
\(\)(\(\dfrac{x^2-3x}{x^2-9}-1\)) : (\(\dfrac{9-x^2}{x^2+x-6}-\dfrac{x-3}{2-x}+\dfrac{x-2}{x+3}\))
rút gọn ạ !!!!
Ta có: \(\left(\dfrac{x^2-3x}{x^2-9}-1\right):\left(\dfrac{9-x^2}{x^2+x-6}-\dfrac{x-3}{2-x}+\dfrac{x-2}{x+3}\right)\)
\(=\left(\dfrac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-1\right):\left(\dfrac{9-x^2+x^2-9+\left(x-2\right)^2}{\left(x-2\right)\left(x+3\right)}\right)\)
\(=\left(\dfrac{x}{x+3}-1\right):\dfrac{x-2}{x+3}\)
\(=\dfrac{x-x-3}{x+3}\cdot\dfrac{x+3}{x-2}\)
\(=\dfrac{-3}{x-2}\)
Đúng 2
Bình luận (0)
Điều kiện : x ≠ 2 ; x ≠ 3 ; x ≠ - 3
\(\left(\dfrac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-1\right):\left(\dfrac{\left(3-x\right)\left(x+3\right)}{\left(x-2\right)\left(x+3\right)}-\dfrac{x-3}{2-x}+\dfrac{x-2}{x+3}\right)\)
\(=\left(\dfrac{x}{x+3}-1\right):\left(\dfrac{9-x^2+\left(x-3\right)\left(x+3\right)+\left(x-2\right)^2}{\left(x-2\right)\left(x+3\right)}\right)\)
\(=\dfrac{x-x-3}{x+3}:\dfrac{9-x^2+x^2-9+\left(x-2\right)^2}{\left(x-2\right)\left(x+3\right)}\)
\(=\dfrac{-3}{x+3}:\dfrac{x-2}{\left(x+3\right)}\)
\(=\dfrac{-3}{x-2}\)
Đúng 1
Bình luận (0)
rút gọn \(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-3}\) với x ≥ 0 , x ≠ 9
Sửa đề: \(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)+2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{x-9}\)
\(=\dfrac{x+3\sqrt{x}+2x+6\sqrt{x}-3x-9}{x-9}\)
\(=\dfrac{9\sqrt{x}-9}{x-9}\)
Đúng 0
Bình luận (0)
Rút gọn B
B=\(\dfrac{x^2+39}{x^2-9}+\dfrac{8}{x+3}+\dfrac{1}{3-x}\)
help
\(B=\dfrac{x^2+39}{\left(x-3\right)\left(x+3\right)}+\dfrac{8}{x+3}-\dfrac{1}{x-3}\)
\(=\dfrac{x^2+39+8x-24-x-3}{\left(x-3\right)\left(x+3\right)}=\dfrac{x^2+7x+12}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{\left(x+3\right)\left(x+4\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{x+4}{x-3}\)
Đúng 1
Bình luận (0)
\(B=\dfrac{x^2+39}{x^2-9}+\dfrac{8}{x+3}+\dfrac{1}{3-x}\) (ĐK: \(x\ne3,x\ne-3\))
\(B=\dfrac{x^2+39}{\left(x+3\right)\left(x-3\right)}+\dfrac{8\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{1}{x-3}\)
\(B=\dfrac{x^2+39+8x-24}{\left(x+3\right)\left(x-3\right)}-\dfrac{1}{x-3}\)
\(B=\dfrac{x^2+8x+15}{\left(x+3\right)\left(x-3\right)}-\dfrac{x+3}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x^2+8x+15-x-3}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{x^2+7x+12}{\left(x+3\right)\left(x-3\right)}\)
\(B=\dfrac{\left(x+3\right)\left(x+4\right)}{\left(x-3\right)\left(x+3\right)}\)
\(B=\dfrac{x+4}{x-3}\)
Đúng 1
Bình luận (0)
rút gọn biểu thức M=\(\dfrac{x+3}{x-9}\)+\(\dfrac{2}{\sqrt{x}+3}\)-\(\dfrac{1}{\sqrt{x}-3}\) với x≥0,x≠9
\(M=\dfrac{x+3+2\left(\sqrt{x}-3\right)-\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(M=\dfrac{x+3+2\sqrt{x}-6-\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(M=\dfrac{x+\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(M=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(M=\dfrac{\sqrt{x}-2}{\sqrt{x}-3}\)
Đúng 1
Bình luận (0)
Ta có: \(M=\dfrac{x+3}{x-9}+\dfrac{2}{\sqrt{x}+3}-\dfrac{1}{\sqrt{x}-3}\)
\(=\dfrac{x+3+2\left(\sqrt{x}-3\right)-\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-\sqrt{x}+2\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x+\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}-3}\)
Đúng 0
Bình luận (0)
Rút gọn phân thức
A=\(\left(\dfrac{x-3}{x}-\dfrac{x}{x-3}+\dfrac{9}{x^2-3x}\right):\dfrac{2x-2}{x}\)
\(\left(\dfrac{x-3}{x}-\dfrac{x}{x-3}+\dfrac{9}{x^2-3x}\right):\dfrac{2x-2}{x}\)
\(=\left(\dfrac{x-3}{x}-\dfrac{x}{x-3}+\dfrac{9}{x\left(x-3\right)}\right):\dfrac{2x-2}{x}\)
\(=\left(\dfrac{\left(x-3\right)^2}{x\left(x-3\right)}-\dfrac{x^2}{x\left(x-3\right)}+\dfrac{9}{x\left(x-3\right)}\right)\cdot\dfrac{x}{2\left(x-1\right)}\)
\(=\dfrac{x^2-6x+9-x^2+9}{x\left(x-3\right)}\cdot\dfrac{x}{2\left(x-1\right)}\)
\(=\dfrac{-6x+18}{x\left(x-3\right)}\cdot\dfrac{x}{2\left(x-1\right)}\\ =\dfrac{-6\left(x-3\right)}{x\left(x-3\right)}\cdot\dfrac{x}{2\left(x-1\right)}\)
\(=\dfrac{-6}{x}\cdot\dfrac{x}{2\left(x-1\right)}\)
\(=\dfrac{-3}{x-1}\)
Đúng 3
Bình luận (1)
RÚT GỌN BIỂU THỨC:
16) \(A = \dfrac{\sqrt{x}}{\sqrt{x} + 3} + \dfrac{2\sqrt{x}}{\sqrt{x} - 3} - \dfrac{3x + 9}{x - 9}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)+2\sqrt{x}\left(\sqrt{x}+3\right)-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{x-9}=\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
Đúng 1
Bình luận (1)
\(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\) (ĐK: \(x\ge0;x\ne9\))
\(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{\left(\sqrt{x}\right)^2-3^2}\)
\(A=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{2\sqrt{x}\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{3x+9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(A=\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{2x+6\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{3x+9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(A=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(A=\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(A=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(A=\dfrac{3}{\sqrt{x}+3}\)
Đúng 2
Bình luận (0)
Rút gọn P :
\(P=x-\dfrac{3}{2}x+1.\left(\dfrac{3.1}{x^2-9-\dfrac{1}{3-x}}\right)\)
Rút gọn
\(C=\dfrac{2}{x+3}+\dfrac{1}{x-3}-\dfrac{8}{x^2-9}\)
tính C khi x = 4
ĐK: \(x\ne\pm3\)
Khi đó:
\(C=\dfrac{2\left(x-3\right)}{x^2-9}+\dfrac{1\left(x+3\right)}{x^2-9}-\dfrac{8}{x^2-9}\\ =\dfrac{2x-6}{x^2-9}+\dfrac{x+3}{x^2-9}-\dfrac{8}{x^2-9}\\ =\dfrac{2x-6+x+3-8}{x^2-9}\\ =\dfrac{3x-11}{x^2-9}\)
Thế x = 4 vào C được:
\(C=\dfrac{3.4-11}{4^2-9}=\dfrac{12-11}{16-9}=\dfrac{1}{7}\)
Đúng 2
Bình luận (0)
Adfrac{X-1}{X+3}+dfrac{2}{X-3}+dfrac{^{X^2}}{9-X^2}nhândfrac{-2}{2x+1} a rút gọn biểu thức b tính giá trị A biết left|x-2right|0
Đọc tiếp
A=\(\dfrac{X-1}{X+3}+\dfrac{2}{X-3}+\dfrac{^{X^2}}{9-X^2}nhân\dfrac{-2}{2x+1}\) a rút gọn biểu thức b tính giá trị A biết \(\left|x-2\right|=0\)
Bạn ghi lại đề đi bạn. Khó hiểu quá!
Đúng 0
Bình luận (0)
rút gọn
\(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{7\sqrt{x}+3}{9-x}\)
ĐKXĐ: x >=0, x khác 9
= \(\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{7\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
= \(\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}+\sqrt{x}+3-7\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
= \(\dfrac{3x-9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
= \(\dfrac{3\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\dfrac{3\sqrt{x}}{\sqrt{x}+3}\)
Đúng 0
Bình luận (0)