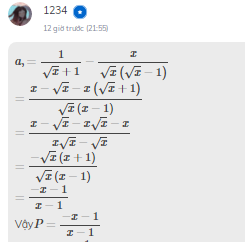
Mk ra đáp án khác với đáp án ủa bn nên bn bào sai chứ j, thật ra cả 2 đáp án đều giống nhau, do biến đổi dấu nên trở thành 2 đáp án khác nhau thôi :V

để mk lm lại phần đáp án của mk ra giống đáp án của bn nek :V

\(a,\)\(P=\dfrac{-x-1}{x-1}\)

\(\Rightarrow\dfrac{-\left(-x-1\right)}{-\left(x-1\right)}=\dfrac{x-1}{-x+1}=\dfrac{x-1}{1-x}\)

Còn câu b thì hôm qua bn ghi là \(x=\dfrac{1}{\sqrt{2}}\) chứ có pk là \(1\sqrt{2}\) đou >:V

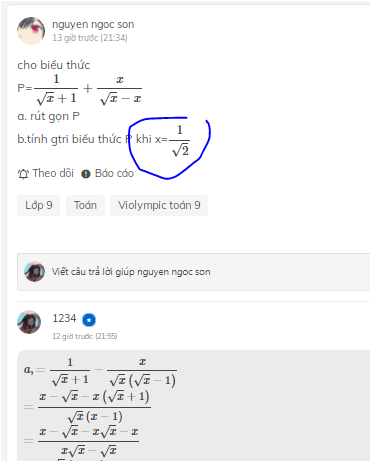
\(b,\)Thay \(x=1\sqrt{2}\) vào \(P\) ta có :

\(P=\dfrac{x-1}{1-x}\)

\(P=\dfrac{1\sqrt{2}-1}{1-1\sqrt{2}}=3+2\sqrt{2}\)

a) \(A=\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right):\left(1-\dfrac{3-\sqrt{x}}{\sqrt{x}+3}\right)\) (ĐK: \(x>0;x\ne1\)) 

\(A=\left[\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\right]:\left(\dfrac{\sqrt{x}+3}{\sqrt{x}+3}-\dfrac{3-\sqrt{x}}{\sqrt{x}+3}\right)\)

\(A=\left(\dfrac{x+\sqrt{x}+1}{\sqrt{x}}-\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\right):\dfrac{\sqrt{x}+3-3+\sqrt{x}}{\sqrt{x}+3}\)

\(A=\dfrac{x+\sqrt{x}+1-x+\sqrt{x}-1}{\sqrt{x}}:\dfrac{2\sqrt{x}}{\sqrt{x}+3}\)

\(A=\dfrac{2\sqrt{x}}{\sqrt{x}}\cdot\dfrac{\sqrt{x}+3}{2\sqrt{x}}\)

\(A=\dfrac{\sqrt{x}+3}{\sqrt{x}}\)

b) Ta có: \(x=\dfrac{1}{6-2\sqrt{5}}=\dfrac{1}{\left(\sqrt{5}\right)^2-2\cdot\sqrt{5}\cdot1+1^2}=\dfrac{1}{\left(\sqrt{5}-1\right)^2}=\left(\dfrac{1}{\sqrt{5}-1}\right)^2\)

Thay vào A ta có:

\(A=\dfrac{\sqrt{\left(\dfrac{1}{\sqrt{5}-1}\right)^2}+3}{\sqrt{\left(\dfrac{1}{\sqrt{5}-1}\right)^2}}=3\sqrt{5}-2\)

c) Ta có: \(\dfrac{\sqrt{x}+3}{\sqrt{x}}=1+\dfrac{3}{\sqrt{x}}\)

\(\Rightarrow\sqrt{x}\in\left\{1;3\right\}\)

\(\Rightarrow x\in\left\{1;9\right\}\)

a: ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x< >1\end{matrix}\right.\)

\(A=\left(\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\dfrac{\sqrt{x}+3+3-\sqrt{x}}{\sqrt{x}+3}\)

\(=\dfrac{x+\sqrt{x}+1-x+\sqrt{x}-1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}+3}{6}\)

\(=\dfrac{2\sqrt{x}}{\sqrt{x}}\cdot\dfrac{\sqrt{x}+3}{6}=\dfrac{\sqrt{x}+3}{3}\)

b: Khi \(x=\dfrac{1}{6-2\sqrt{5}}=\dfrac{6+2\sqrt{5}}{16}=\left(\dfrac{\sqrt{5}+1}{4}\right)^2\) thì \(A=\dfrac{\dfrac{\sqrt{5}+1}{4}+3}{3}=\dfrac{\sqrt{5}+1+12}{12}=\dfrac{13+\sqrt{5}}{12}\)

c: A là số nguyên

=>\(\sqrt{x}+3⋮3\)

=>\(\sqrt{x}⋮3\)

=>\(x=k^2\);\(k\in Z\)

Kết hợp ĐKXĐ, ta được: x là số chính phương và x>0 và \(x\ne1\)

x\(\le\)11

=>3(x-1)-2(x-2)<=6/4(x-3)

=>3x-3-2x+4<=3/2x-9/2

=>-1/2x<=-9/2-1=-11/2

=>x>=11

Lời giải:

\(\frac{2x-2\sqrt{x}+2}{x-\sqrt{x}}=\frac{2(x-\sqrt{x})+2}{x-\sqrt{x}}=\frac{2(x-\sqrt{x})+2}{x-\sqrt{x}}=2+\frac{2}{x-\sqrt{x}}\)

\(\dfrac{2x-2\sqrt{x}+2}{x\sqrt{x}+1}=\dfrac{2}{\sqrt{x}+1}\)

1) \(P=\dfrac{\sqrt{x}.\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)

\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}=\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}\)

2) \(P=\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}=\dfrac{\left(\sqrt{3+2\sqrt{2}}+1\right)^2}{\sqrt{3+2\sqrt{2}}}\)

\(=\dfrac{\left(\sqrt{\left(\sqrt{2}+1\right)^2}+1\right)^2}{\sqrt{\left(\sqrt{2}+1\right)^2}}=\dfrac{\left(\sqrt{2}+2\right)^2}{\sqrt{2}+1}=\dfrac{2+4+4\sqrt{2}}{\sqrt{2}+1}=\dfrac{6+4\sqrt{2}}{\sqrt{2}+1}\)

với những dạng như thế này mà tn thì bạn nên thay thẳng vào luôn nha