Cho hàm số: y = x 3 − (m + 4) x 2 − 4x + m (1). Xác định k để (C) cắt đường thẳng y = kx tại ba điểm phân biệt.

Những câu hỏi liên quan
Bài 1: Tìm m để các hàm số sau là hàm số bậc nhất a) y ( m - 2 )x - dfrac{2}{3} b) y ( 4 - 2022m )x - 2 c) y sqrt{1-2m}x + m - 3Bài 2: Cho đồ thị hàm số y -2x + 3a) Xác định hệ số a,bb) Các điểm A( -2 ; 7) ; B(sqrt{2} ; 6)c) Tìm tọa độ điểm M thuộc ( d ) có tung độ 11d) Tìm tọa độ điểm C thuộc ( d ), biết rằng hoành độ của điểm C gấp 3 tung độ của nóe) Tìm tọa độ điểm E thuộc ( d ), biết rằng tung độ của điểm E và hoành độ là 2 số đối nhau
Đọc tiếp
Bài 1: Tìm m để các hàm số sau là hàm số bậc nhất
a) y= ( m - 2 )x - \(\dfrac{2}{3}\) b) y= ( 4 - 2022m )x - 2 c) y= \(\sqrt{1-2m}\)x + m - 3
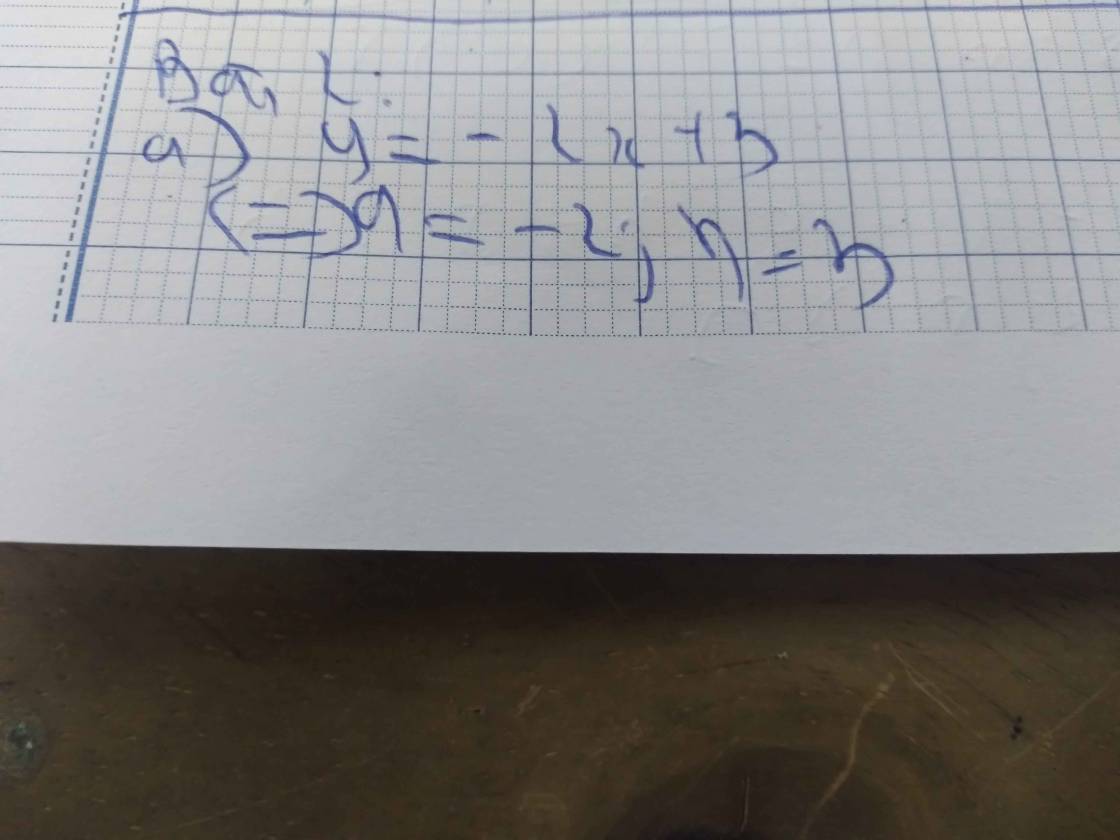
Bài 2: Cho đồ thị hàm số y= -2x + 3
a) Xác định hệ số a,b
b) Các điểm A( -2 ; 7) ; B(\(\sqrt{2}\) ; 6)
c) Tìm tọa độ điểm M thuộc ( d ) có tung độ = 11
d) Tìm tọa độ điểm C thuộc ( d ), biết rằng hoành độ của điểm C gấp 3 tung độ của nó
e) Tìm tọa độ điểm E thuộc ( d ), biết rằng tung độ của điểm E và hoành độ là 2 số đối nhau
Cho hàm số y : (m+1) x +m-1 (d) (m khác -1, m là tham số)
a) Xác định m để đồ thị hàm số đã cho đi qua (7;2)
b) Xác định m để đường thẳng cắt đường thẳng y = 3x-4 tại điểm có hoành độ = 2
c) Xác định m để đường thẳng đồng quy với 2 đường thẳng d1 : y= 2x-1 và d2 : y=x-8
Xem chi tiết
Bài1. cho hàm số: y= k.x+3-2x+k
a) xác định k để hàm số đã cho là hàm số bậc nhất
b) xác định k để hàm số đồng biến trên R
Bài2. cho đường thẳng \(y=\left(2m-3\right)x-\dfrac{1}{2}\) (P) tìm m để đường thẳng D đi qua điểm \(A\left(\dfrac{-1}{2};\dfrac{2}{3}\right)\)
Bài 1:
a) Để hàm số y=(k-2)x+k+3 là hàm số bậc nhất thì \(k\ne2\)
b) Để hàm số y=(k-2)x+k+3 đồng biến trên R thì k-2>0
hay k>2
Bài 2:
Thay \(x=-\dfrac{1}{2}\) và \(y=\dfrac{2}{3}\) vào (D), ta được:
\(\left(2m-3\right)\cdot\dfrac{-1}{2}-\dfrac{1}{2}=\dfrac{2}{3}\)
\(\Leftrightarrow\left(2m-3\right)\cdot\dfrac{-1}{2}=\dfrac{2}{3}+\dfrac{1}{2}=\dfrac{7}{6}\)
\(\Leftrightarrow2m-3=\dfrac{7}{6}:\dfrac{-1}{2}=\dfrac{-7}{6}\cdot\dfrac{2}{1}=-\dfrac{14}{6}=-\dfrac{7}{3}\)
\(\Leftrightarrow2m=\dfrac{-7}{3}+3=\dfrac{-7}{3}+\dfrac{9}{3}=\dfrac{2}{3}\)
hay \(m=\dfrac{1}{3}\)
Đúng 0
Bình luận (0)
Cho hàm số y = (3 – m)x2a) Tìm điều kiện của m để hàm số trên được xác định.b) Xác định m để hàm số đồng biến với mọi x < 0.c) Xác định m để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0.
a, ĐKXĐ để hàm được xác định : \(3-m\ne0\)
\(\Leftrightarrow m\ne3\)
b, - Với x < 0 để hàm số đồng biến thì : \(3-m< 0\)
\(\Leftrightarrow m>3\)
Vậy ...
c, - Để y = 0 là giá trị nhỏ nhất của hàm số tại x = 0
\(\Leftrightarrow a>0\)
\(\Leftrightarrow3-m>0\)
\(\Leftrightarrow m< 3\)
Vậy ...
Đúng 2
Bình luận (0)
a) Để hàm số \(y=\left(3-m\right)x^2\) được xác định thì \(3-m\ne0\)
hay \(m\ne3\)
b) Để hàm số \(y=\left(3-m\right)x^2\) đồng biến với mọi x<0 thì \(3-m< 0\)
\(\Leftrightarrow m>3\)
c) Để y=0 là giá trị nhỏ nhất của hàm số tại x=0 thì 3-m>0
hay m<3
Đúng 2
Bình luận (0)
Cho hàm số bậc nhất: y = (m – 1)x + 3 (1) (với m ≠ 1) a) Xác định m để hàm số (1) đồng biến trên R b) Xác định m, biết đồ thị của hàm số (1) song song với đường thẳng y = – x + 1 c) Xác định m để đường thẳng (d1): y = 1 – 3x; (d2): y = – 0,5x – 1,5 và đồ thị của hàm số (1) cùng đi qua một điểm.
Đây nhé bn !
3. Tìm tập xác định của các hàm số sau:a) y 2^{x^2-1}b) y x^{-4}c) y (x-1)^{-3}d) y (x^2-1)^{4pi}e) y ln (4x^2-1)f) y log_{3} (x^2-2)h) y (2x^2-4x)^{frac{-1}{3}}k) y (2x-1)^{-4}l) y log_{3} (x^2-1) + ln (x-2) + e^{frac{x}{x-1}}
Đọc tiếp
3. Tìm tập xác định của các hàm số sau:
a) \(y = 2^{x^2-1}\)
b) \(y = x^{-4}\)
c) \(y = (x-1)^{-3}\)
d) \(y = (x^2-1)^{4\pi}\)
e) \(y = \ln (4x^2-1)\)
f) \(y = \log_{3} (x^2-2)\)
h) \(y = (2x^2-4x)^{\frac{-1}{3}}\)
k) \(y = (2x-1)^{-4}\)
l) \(y = \log_{3} (x^2-1) + \ln (x-2) + e^{\frac{x}{x-1}}\)
`a)TXĐ: R`
`b)TXĐ: R\\{0}`
`c)TXĐ: R\\{1}`
`d)TXĐ: (-oo;-1)uu(1;+oo)`
`e)TXĐ: (-oo;-1/2)uu(1/2;+oo)`
`f)TXĐ: (-oo;-\sqrt{2})uu(\sqrt{2};+oo)`
`h)TXĐ: (-oo;0) uu(2;+oo)`
`k)TXĐ: R\\{1/2}`
`l)ĐK: {(x^2-1 > 0),(x-2 > 0),(x-1 ne 0):}`
`<=>{([(x > 1),(x < -1):}),(x > 2),(x ne 1):}`
`<=>x > 2`
`=>TXĐ: (2;+oo)`
Đúng 2
Bình luận (2)
Câu 2: Cho hàm số: y = (m+1)x - 2m (d)
a) Xác định m để hàm số trên là hàm số nghịch biến?
b) Vẽ đồ thị hàm số trên khi m = 1
c) Xác định m để đồ thị hàm số trên song song với đường thẳng y = 3x + 6?
Hàm số y = (m+1)x -2m là hàm bậc nhất khi m+1 ≠ 0 ⇔ m ≠ - 1
a) Hàm số nghịch biến trên R khi a < 0 ⇔ m + 1< 0 ⇔ m < - 1
kết hợp với điều kiện. Vậy m < -1
b) Khi m = 1 ta được: y = (1+1)x - 2.1 hay y = 2x - 2
Đồ thị hàm số y = 2x - 2 đi qua hai điểm A(0;-2) và B(1;0)
c) Đồ thị của hai hàm số song song với nhau khi \(\left\{{}\begin{matrix}a=a'\\b\ne b'\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m+1=3\\-2m\ne6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2\\m\ne-3\end{matrix}\right.\)
kết hợp với điều kiện. Vậy m = 2
Đúng 2
Bình luận (0)
Tham Khảo:
Hàm số y = (m+1)x -2m là hàm bậc nhất khi m+1 ≠ 0 ⇔ m ≠ - 1
a) Hàm số nghịch biến trên R khi a < 0 ⇔ m + 1< 0 ⇔ m < - 1
kết hợp với điều kiện. Vậy m < -1
b) Khi m = 1 ta được: y = (1+1)x - 2.1 hay y = 2x - 2
Đồ thị hàm số y = 2x - 2 đi qua hai điểm A(0;-2) và B(1;0)
c) Đồ thị của hai hàm số song song với nhau khi
kết hợp với điều kiện. Vậy m = 2
Đúng 1
Bình luận (0)
3) cho hàm số bậc nhất \(y=\left(2-m\right).x+2m-1\) (d)
a) với m=1 hãy vẽ đồ thị
b) xác định m để (d) đi qua trung điểm của 2 đường thẳng \(y=-x+3\) và \(y=-2x+1\)
c) xác định m để (d) cắt đường thẳng \(y=x-2\) tại điểm có hoành độ -1
Lời giải:
a. Với $m=1$ thì ptđt $(d)$ là: $y=x+1$
b. Trung điểm của 2 đường thẳng??? Đường thẳng thì làm gì có trung điểm hả bạn? Đoạn thẳng thì có.
c. $(d)$ cắt $y=x-2$ tại điểm có hoành độ $-1$
$\Leftrightarrow$ PT hoành độ giao điểm $(2-m)x+2m-1-(x-2)=0$ nhận $x=-1$ là nghiệm
$\Leftrightarrow (2-m)(-1)+2m-1-(-1-2)=0$
$\Leftrightarrow m=0$
Đúng 0
Bình luận (0)
Bài 1: a) Cho hàm số f(x) (a- 1)x + b. Xác định hàm số biết f(-1) 2014 ; f(2) 2017b) Tìm m;n để đa thức P(x) mx3 + (m + 2)x2 - (3n - 5)x - 4n đồng thời chia hết cho x + 1 và x - 3Bài 2: Cho đường thẳng (d): y 4xviết phương trình đường thẳng (d1) song song với đường thẳng (d) và có tung độ gốc bằng 10Bài 3: Xác định a;b để đồ thị hàm số y ax + b đi qua A(3;-1) và B(-3;2)Bài 4: Cho 2 hàm số bậc nhất y x - m và y -2x + m - 1a) Xác định tọa độ giao điểm của đồ thị 2 hàm số khi m 2b) Vẽ đồ...
Đọc tiếp
Bài 1: a) Cho hàm số f(x) = (a- 1)x + b. Xác định hàm số biết f(-1) = 2014 ; f(2) = 2017
b) Tìm m;n để đa thức P(x) = mx3 + (m + 2)x2 - (3n - 5)x - 4n đồng thời chia hết cho x + 1 và x - 3
Bài 2: Cho đường thẳng (d): y = 4x
viết phương trình đường thẳng (d1) song song với đường thẳng (d) và có tung độ gốc bằng 10
Bài 3: Xác định a;b để đồ thị hàm số y = ax + b đi qua A(3;-1) và B(-3;2)
Bài 4: Cho 2 hàm số bậc nhất y = x - m và y = -2x + m - 1
a) Xác định tọa độ giao điểm của đồ thị 2 hàm số khi m = 2
b) Vẽ đồ thị 2 hàm số trên khi m = 2
c) Tìm m để đồ thị 2 hàm số cắt nhau tại 1 điểm trên trục tung
Bài 5: Viết phương trình đường thẳng (d) có hệ số góc bằng 7 và đi qua điểm M(2;-1)
Bài 6: Cho 3 đường thẳng: (d1): y = -2x + 3; (d2): y = 3x - 2; (d3): y = m(x + 1) - 5
a) Tìm m để 3 đường thẳng đã cho đồng quy
b) Chứng minh rằng đường thẳng (d3) luôn đi qua 1 điểm cố định khi m thay đổi