Cho ba số thực a, b, c biết P = 3 4 log b c a 2 b c + log a b 2 b 2 c a + 3 4 log a c c 2 a b đạt giá trị nhỏ nhất tại bộ số a 0 ; b 0 ; c 0 . Giá trị của 6 a 0 + 4 b 0 + 2 c 0 có thể bằng:
A. 7
B. 6
C. 16 3
D. 9
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit \(y = {\log _a}x;\,y = {\log _b}x;\,y = {\log _c}x\) được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?
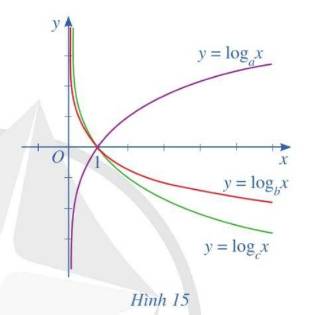
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a
Hoạt động 5
Cho ba số thực dương a, b, c với \(a \ne 1\,;\,c \ne 1\)
a) Bằng cách sử dụng tính chất \(b = {a^{{{\log }_a}b}}\), chứng tỏ rằng \({\log _c}b = {\log _a}b.{\log _c}a\)
b) So sánh \({\log _a}b\,\,\,và \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)
a) \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {a^{{{\log }_c}b}} = {a^{{{\log }_a}b.{{\log }_c}a}} \Leftrightarrow {c^{{{\log }_c}b}} = {\left( {{c^{{{\log }_c}a}}} \right)^{{{\log }_a}b}} \Leftrightarrow b = {a^{{{\log }_a}b}} \Leftrightarrow b = b\) (luôn đúng)
Vậy \({\log _c}b = {\log _a}b.{\log _c}a\)
b) Từ \({\log _c}b = {\log _a}b.{\log _c}a \Leftrightarrow {\log _a}b = \frac{{{{\log }_c}b}}{{{{\log }_c}a}}\)
Cho hai số thực dương a, b với \(a \ne 1\). Khẳng định nào sau đây là đúng?
A. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + {\log _a}b\).
B. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + 2{\log _a}b\).
C. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{3}{2} + {\log _a}b\).
D. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{1}{3} + \frac{1}{2}{\log _a}b\).
\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B
Cho đồ thị ba hàm số \(y = {\log _a}x,y = {\log _b}x\) và \(y = {\log _c}x\) như hình bên. Mệnh đề nào sau đây là đúng?
A. \(a > b > c\).
B. \(b > a > c\).
C. \(a > b > c\).
D. \(b > c > a\).
Hàm số \(y=log_cx\) nghịch biến
\(\Rightarrow0< c< 1\) và các hàm \(y=log_ax,y=log_bx\) đồng biến nên \(a,b>1\)
Ta chọn \(x=100\Rightarrow log_a>log_b100\Rightarrow a< b\Rightarrow b>a>c\)
\(\Rightarrow B\)
\(log_cx\) nghịch biến biến nên 0<c<1
\(log_ax;log_bx\) đồng biến nên a>1; b>1
=>Loại D
\(log_ax>log_bx\left(x>1\right)\)
=>\(\dfrac{1}{log_xa}< \dfrac{1}{log_xb}\)
=>a<b
=>Chọn B
1) Cho a,b là các số thực dương khác 1 và thoả mãn ab khác 1. Rút gọn biểu thức sau: P=(logab + logba + 2)(logab - logabb).logba - 1
Cho bốn số thực dương a, b, x, y với \(a,b \ne 1\). Khẳng định nào sau đây là sai?
A. \({\log _a}(xy) = {\log _a}x + {\log _b}y\).
B. \({\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y\).
C. \({\log _a}\frac{1}{x} = \frac{1}{{{{\log }_a}x}}\).
D. \({\log _a}b \cdot {\log _b}x = {\log _a}x\).
1. cho a=log3 2 và b=log3 5. tính các logarit sau theo a, b; A=log3 80, B=log3 37,5
2. cho log10 3=a, log5=b. tính C=log30 8 theo a, b
3. cho log27 5=a, log8 7=b, log2 3=c. tính D log6 35 theo a, b, c
Bài 1:
\(A=\log_380=\log_3(2^4.5)=\log_3(2^4)+\log_3(5)\)
\(=4\log_32+\log_35=4a+b\)
\(B=\log_3(37,5)=\log_3(2^{-1}.75)=\log_3(2^{-1}.3.5^2)\)
\(=\log_3(2^{-1})+\log_33+\log_3(5^2)=-\log_32+1+2\log_35\)
\(=-a+1+2b\)
Bài 2:
\(\log_{30}8=\frac{\log 8}{\log 30}=\frac{\log (2^3)}{\log (10.3)}=\frac{3\log2}{\log 10+\log 3}\)
\(=\frac{3\log (\frac{10}{5})}{1+\log 3}=\frac{3(\log 10-\log 5)}{1+\log 3}=\frac{3(1-b)}{1+a}\)
Bài 3:
\(\log_{27}5=a; \log_87=b; \log_23=c\)
\(\Leftrightarrow \frac{\ln 5}{\ln 27}=a; \frac{\ln 7}{\ln 8}=b; \frac{\ln 3}{\ln 2}=c\)
\(\Leftrightarrow \frac{\ln 5}{\ln (3^3)}=a; \frac{\ln 7}{\ln (2^3)}=b; \ln 3=c\ln 2\)
\(\Leftrightarrow \frac{\ln 5}{3\ln 3}=a; \frac{\ln 7}{3\ln 2}=b; \ln 3=c\ln 2\)
\(\Rightarrow \frac{\ln 5}{3c\ln 2}=a; \frac{\ln 7}{3\ln 2}=b\)
\(\Rightarrow \ln 35=\ln 5+\ln 7=3ac\ln 2+3b\ln 2\)
Do đó:
\(D=\log_6 35=\frac{\ln 35}{\ln 6}=\frac{\ln 35}{\ln 2+\ln 3}=\frac{\ln 35}{\ln 2+c\ln 2}=\frac{3ac\ln 2+3b\ln 2}{\ln 2+c\ln 2}\)
\(=\frac{3ac+3b}{1+c}\)
Cho các số thực dương a,b thỏa mãn log a = x , log b = y . Tính P = log ( a 2 b 3 )
![]()
![]()
![]()
![]()
Cho ba số thực a,b,c thỏa mãn a+b+c=3. CMR :
\(a^4+b^4+c^4\ge a^3+b^3+c^3\)
Áp dụng BĐT đúng cho mọi số thực \(x^2+y^2+z^2\ge\frac{1}{3}\left(x+y+z\right)^2\)
\(a^4+b^4+c^4\ge\frac{1}{3}\left(a^2+b^2+c^2\right)^2\ge\frac{1}{27}\left(a+b+c\right)^4=3\)
\(\Rightarrow4\left(a^4+b^4+c^4\right)\ge3\left(a^4+b^4+c^4\right)+3\) (1)
Mặt khác: \(a^4+a^4+a^4+1\ge4\left|a^3\right|\ge4a^3\)
Tương tự và cộng lại: \(3\left(a^4+b^4+c^4\right)+3\ge4\left(a^3+b^3+c^3\right)\) (2)
(1);(2) \(\Rightarrow4\left(a^4+b^4+c^4\right)\ge4\left(a^3+b^3+c^3\right)\)
Cho a,b,c là các số thực dương thỏa mãn a log 5 2 = 4 , b log 4 6 = 1 , log , c log 7 3 = 49 Tính giá trị của biểu thức T = a log 2 2 5 + b log 4 2 6 + 3 c log 7 2 3
A. T=126
B. T = 5 + 2 3
C. T=88
D. T = 3 - 2 3