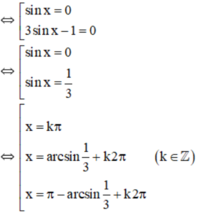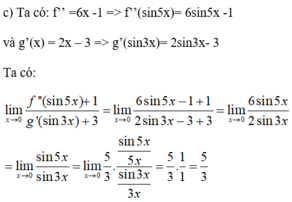Cho f x = x - 3 x . Giải phương trình f'(x)=0
A. 0
B. ln3
C. log 1 3 ln 3
D. x = 3 ln 3
cho hàm số \(f\left(x\right)=x^3-3x^2+2\)
a, giải bất phương trình \(f'\left(x\right)\le0\)
b, giải phương trình \(f'=\left(x^2-3x+2\right)=0\)
c, đặt \(g\left(x\right)=f\left(1-2x\right)+x^2-x+2022\) giải bất phương trình\(g'\left(x\right)\ge0\)
\(a,f'\left(x\right)=3x^2-6x\\ f'\left(x\right)\le0\Leftrightarrow3x^2-6x\le0\\ \Leftrightarrow3x\left(x-2\right)\le0\Leftrightarrow0\le x\le2\)
Lời giải:
a. $f'(x)\leq 0$
$\Leftrightarrow 3x^2-6x\leq 0$
$\Leftrightarrow x(x-2)\leq 0$
$\Leftrightarrow 0\leq x\leq 2$
b.
$f'(x)=x^2-3x+2=0$
$\Leftrightarrow 3x^2-6x=x^2-3x+2=0$
$\Leftrightarrow 3x(x-2)=(x-1)(x-2)=0$
$\Leftrightarrow x-2=0$
$\Leftrightarrow x=2$
c.
$g(x)=f(1-2x)+x^2-x+2022$
$g'(x)=(1-2x)'f(1-2x)'_{1-2x}+2x-1$
$=-2[3(1-2x)^2-6(1-2x)]+2x-1$
$=-24x^2+2x+5$
$g'(x)\geq 0$
$\Leftrightarrow -24x^2+2x+5\geq 0$
$\Leftrightarrow (5-12x)(2x-1)\geq 0$
$\Leftrightarrow \frac{-5}{12}\leq x\leq \frac{1}{2}$
Cho hàm số y= f(x)=x^3-2x^2 (C) a) Tìm f'(x). Giải bất phương trình f'(x)>0 b) Viết phương trình tiếp tuyến của (C) tại điểm M có hoành độ x0=2
Cho hàm số y = f(x)=x^3-2x^2(C) a) tìm f'(x) . Giải bất phương trình f'(x)>0 b) viết phương trình tiếp tuyến của (C) tại điểm M có hoành độ x0=2
\(f'\left(x\right)=3x^2-4x\)
\(f'\left(x\right)>0\Leftrightarrow3x^2-4x>0\Rightarrow\left[{}\begin{matrix}x>\dfrac{4}{3}\\x< 0\end{matrix}\right.\)
\(f'\left(2\right)=4\) ; \(f\left(2\right)=0\)
Phương trình tiếp tuyến:
\(y=4\left(x-2\right)+0\Leftrightarrow y=4x-8\)
Cho hàm số: \(f(x)=\dfrac{1}{3}x^3−\dfrac{1}{2}x^2−4x+6\)
a) Giải phương trình \(f’(\sin x) = 0\)
b) Giải phương trình \(f’’(\cos x) = 0\)
c) Viết phương trình tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ là nghiệm của phương trình \(f’’(x) = 0\)
Cho hàm số f (x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) và f ' ( x ) = 1 x 2 + x , f ( 1 ) = ln 1 2 . Biết ∫ 1 2 ( x 2 + 1 ) f ( x ) d x = a ln 3 + b ln 2 + c với a,b,c là các số hữu tỉ. Giá trị biểu thức a+b+c bằng
A. 27 2
B. 1 6
C. 7 6
D. - 3 2
Bài 1: Giải các phương trình
|
|
a/ ![]() c/
c/ ![]()
b/ ![]() d/
d/ ![]()
e/ (x +![]() )(x-
)(x-![]() ) = 0 g/ (3x-1)(2x-3)(x+5) = 0
) = 0 g/ (3x-1)(2x-3)(x+5) = 0
h/ x2 – x = 0
f/ x2 – 2x = 0 i/ x2 – 3x = 0 k/ (x+1)(x+2) =(2-x)(x+2)
Bài 4: Giải các phương trình sau:
g) ![]() h)
h)![]()
n)  m)
m)
i/ ![]() = 8 – x k)
= 8 – x k) ![]() = – 4x +7
= – 4x +7
f. ![]()
Bài 6: Giải các bất phương trình sau và biểu diễn nghiệm trên trục số:
j/ 3x - (2x + 5 ) £ (2x – 3 ) k/ (x – 3)(x + 3) < x(x + 2 ) + 3
p/ 1+![]() q)
q) ![]()
b. ![]()
6:
k: =>x^2-9<x^2+2x+3
=>2x+3>-9
=>2x>-12
=>x>-6
1:
h: =>x(x-1)=0
=>x=0; x=1
i: =>x(x-3)=0
=>x=0; x=3
Cho f(x)=x^2 -2(m-2)x+m+10. Định m để:
a. Phương trình f(x)=0 có một nghiệm x= 1 và tính nghiệm kia
b. Phương trình f(x)=0 có nghiệm kép. Tính nghiệm kép đó.
c. Tìm m để phương trình f(x)=0 có 2 nghiệm âm phân biệt.
d. Tìm m để f(x)<0 có nghiệm đúng với mọi xϵR
a.
\(f\left(x\right)=0\) có nghiệm \(x=1\Rightarrow f\left(1\right)=0\)
\(\Rightarrow1-2\left(m-2\right)+m+10=0\)
\(\Rightarrow m=15\)
Khi đó nghiệm còn lại là: \(x_2=\dfrac{m+10}{x_1}=\dfrac{25}{1}=25\)
b.
Pt có nghiệm kép khi: \(\Delta'=\left(m-2\right)^2-\left(m+10\right)=0\)
\(\Rightarrow m^2-5m-6=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=6\end{matrix}\right.\)
Với \(m=-1\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=-3\)
Với \(m=6\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=4\)
c.
Pt có 2 nghiệm âm pb khi:
\(\left\{{}\begin{matrix}\Delta'=m^2-5m-6>0\\x_1+x_2=2\left(m-2\right)< 0\\x_1x_2=m+10>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -1\\m>6\end{matrix}\right.\\m< 2\\m>-10\end{matrix}\right.\) \(\Rightarrow-10< m< -1\)
d.
\(f\left(x\right)< 0;\forall x\in R\Rightarrow\left\{{}\begin{matrix}a=1< 0\left(\text{vô lý}\right)\\\Delta'=m^2-5m-6< 0\end{matrix}\right.\)
Không tồn tại m thỏa mãn
Cho các hàm số
f ( x ) = x 3 + b x 2 + c x + d ( C )
g ( x ) = x 2 − 3 x − 1 .
a) Xác định b, c, d sao cho đồ thị (C) đi qua các điểm (1; 3), (−1; −3) và f′(1/3) = 5/3 ;
b) Viết phương trình tiếp tuyến của (C) tại điểm có hoành độ x 0 = 1 ;
c) Giải phương trình f′(sint) = 3;
d) Giải phương trình f′′(cost) = g′(sint);
e) Tìm giới hạn lim z → 0 f ' ' sin 5 z + 2 g ' sin 3 z + 3
Bài 1: Giải các phương trình sau:
a) x - 2 = 0 b)x² – 2x =0
e) 2x² +5x +3= 0 f) x² –x-12 =0
a) \(x-2=0\Leftrightarrow x=2\)
b) \(x^2-2x=0\Leftrightarrow x\left(x-2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
e) \(2x^2+5x+3=0\Leftrightarrow\left(2x+3\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=-1\end{matrix}\right.\)
f) \(x^2-x-12=0\Leftrightarrow\left(x-4\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Cho hàm số f ( x = x 3 + b x 2 + c x + d , C g x = x 2 - 3 x + 1
Với các số b, c, d tìm được ở bài 19, hãy:
a) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x = - 1 .
b) Giải phương trình f ' sin x = 0 .
c) tính lim x → 0 f ' ' sin 5 x + 1 g ' sin 3 x + 3
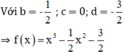
a) f’(x) = 3x2 – x.
⇒ f’(-1) = 4; f(-1) = -3.
⇒ Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = -1 là:
y = 4.(x + 1) – 3 = 4x + 1.
b) f’(sin x) = 0
⇔ 3.sin2x – sin x = 0
⇔ sin x.(3sin x – 1) = 0