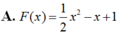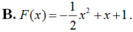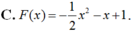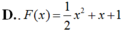Cho hàm số f x = x 2 + n x < 1 2 m x - 3 x > 1 m + 3 x = 1
liên tục tại điểm x = 1. Tính m - n 2018 + m + 1 n 2019
A. 0
B. 1
C. -1
D. 2
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Những câu hỏi liên quan
Cho hàm số f(x)=(x^2 +1)/x^3 -4x .Tính đạo hàm cấp n=30 tại x=1 của hàm số f(x)
Xem chi tiết
Trước hết ta xét: \(g\left(x\right)=\dfrac{1}{x+a}=\left(x+a\right)^{-1}\) với a là hằng số bất kì
\(g'\left(x\right)=-1.\left(x+a\right)^{-2}=\left(-1\right)^1.1!.\left(x+a\right)^{-\left(1+1\right)}\)
\(g''\left(x\right)=-1.\left(-2\right).\left(x+a\right)^{-3}=\left(-1\right)^2.2!.\left(x+a\right)^{-\left(2+1\right)}\)
Từ đó ta dễ dàng tổng quát được:
\(g^{\left(n\right)}\left(x\right)=\left(-1\right)^n.n!.\left(x+a\right)^{-\left(n+1\right)}=\dfrac{\left(-1\right)^n.n!}{\left(x+a\right)^{n+1}}\)
Xét: \(f\left(x\right)=\dfrac{x^2+1}{x\left(x-2\right)\left(x+2\right)}=-\dfrac{1}{4}.\left(\dfrac{1}{x}\right)+\dfrac{5}{8}\left(\dfrac{1}{x+2}\right)+\dfrac{5}{8}\left(\dfrac{1}{x-2}\right)\)
Áp dụng công thức trên ta được:
\(f^{\left(30\right)}\left(1\right)=\dfrac{1}{4}.\dfrac{\left(-1\right)^{30}.30!}{1^{31}}+\dfrac{5}{8}.\dfrac{\left(-1\right)^{30}.30!}{\left(1+2\right)^{31}}+\dfrac{5}{8}.\dfrac{\left(-1\right)^{30}.30!}{\left(1-2\right)^{31}}\)
Bạn tự rút gọn kết quả nhé
Đúng 2
Bình luận (1)
\(f\left(x\right)=\dfrac{x^2+1}{x^3}-4x\) hay \(f\left(x\right)=\dfrac{x^2+1}{x^3-4x}\) bạn?
Đúng 1
Bình luận (1)
Cho hàm số f(x) = mx^2 +2x +2 khi x>0 và nx +2 khi x<=0. Tìm tất cả các giá trị của các tham số m,n sao cho f(x) có đạo hàm tại x=0
Để hàm số có đạo hàm tại x=0 phải thỏa mãn 2 điều kiện, đó là hàm số liên tục tại x=0 và có đạo hàm bên trái bằng đạo hàm bên phải
Để hàm số liên tục tại x=0 \(\Leftrightarrow\lim\limits_{x\rightarrow0^+}=\lim\limits_{x\rightarrow0^-}=f\left(0\right)\Leftrightarrow2=2\left(tm\right)\)
\(f'\left(0^+\right)=\lim\limits_{x\rightarrow0^+}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0^+}\dfrac{mx^2+2x+2-2}{x}=\lim\limits_{x\rightarrow0^+}\dfrac{x\left(mx+2\right)}{x}=2\)
\(f'\left(0^-\right)=\lim\limits_{x\rightarrow0^-}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0^-}\dfrac{nx+2-2}{x}=n\)
\(\Rightarrow\left\{{}\begin{matrix}m\in R\\n=2\end{matrix}\right.\)
\(f\left(0^+\right)=f\left(0^-\right)\Leftrightarrow n=2\)
Đúng 2
Bình luận (0)
Cho hàm số f(x) - x^2 + 3x - 1
a, tính f(-2) , f(-1)
b, Điểm nào dưới đây không thuộc đồ thị hàm số: M (-1; -3), N(1;3), H(3;1)
a: \(f\left(-2\right)=\left(-2\right)^2+3\cdot\left(-2\right)-1\)
=4-6-1
=-3
\(f\left(-1\right)=\left(-1\right)^2+3\cdot\left(-1\right)-1\)
\(=1-3-1\)
=-3
Đúng 0
Bình luận (0)
b: \(F\left(-1\right)=-\left(-1\right)^2+3\cdot\left(-1\right)-1\)
\(=-1-3-1=-5\)
Vậy: M(-1;-3) không thuộc đồ thị
\(F\left(1\right)=-1^2+3\cdot1-1\)
\(=-1+3-1\)
=1
Vậy: N(1;3) không thuộc đồ thị
\(F\left(3\right)=-3^2+3\cdot3-1=-9+6-1=-4\)
Vậy: H(3;1) không thuộc đồ thị
Đúng 1
Bình luận (0)
a) cho hàm số y=(f)x=x^6+1/x^3.cmr f(1/2)=f(x)
b) cho hàm số y=(f)x=x^2+1/x^2.CMR f(x)=f(-x)
c) cho hàm số y=(f)x=5^x. Tính f(x+1)-f(x)
HELPPPPPPPPPPPPP ME!
SGK Cánh Diều
13 tháng 8 2023 lúc 22:35
Cho hàm số \(f(x) = {2^{3x + 2}}\)
a) Hàm số f(x) là hàm hợp của hàm số nào?
b) Tìm đạo hàm của f(x)
a) Hàm số f(x) là hàm hợp của hàm số \(y = {a^x}\)
b) \(f'(x) = \left( {{2^{3x + 2}}} \right)' = \left( {3x + 2} \right)'{.2^{3x + 2}}.\ln 2 = {3.2^{3x + 2}}.\ln 2\)
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
(
x
-
1
)
2
(
m
x
2
+
4
m
x
-
m
+
n
-
2
)
với
m
,
n
∈
R
. Biết trên khoảng...
Đọc tiếp
Cho hàm số f ( x ) = ( x - 1 ) 2 ( m x 2 + 4 m x - m + n - 2 ) với m , n ∈ R . Biết trên khoảng - 7 6 ; 0 hàm số đạt cực đại tại x = -1 Trên đoạn - 7 2 ; 5 4 hàm số đã cho đạt cực tiểu tại.
A. x = - 7 2
B. x = - 3 2
C. x = - 5 2
D. x = - 5 4
Bài 1: Xét tính đơn điệu của hàm số yf(x) khi biết đạo hàm của hàm số là:a) f(x)(x+1)(1-x^2)(2x-1)^3b) f(x)(x+2)(x-3)^2(x-4)^3Bài 2: Cho hàm số yf(x) có đạo hàm f(x)x(x+1)(x-2). Xét tính biến thiên của hàm số:a) yf(2-3x)b) yf(x^2+1)c) yf(3x+1)
Đọc tiếp
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
Cho
f
(
x
)
−
2
x
+
2
;
g
(
x
)
3
x
+
1
Tìm
M
(
x
0
;
y
0...
Đọc tiếp
Cho f ( x ) = − 2 x + 2 ; g ( x ) = 3 x + 1
Tìm M ( x 0 ; y 0 ) biết N ( x 0 ; 2 ) thuộc đồ thị hàm số f(x), P ( 3 ; y 0 ) thuộc đồ thị hàm số g(x)
A. M (1;10)
B. M (0;-10)
C. M (0;10)
D. M (10;0)
Cho hàm số f(x) có đạo hàm f ’ ( x ) = x ( x - 1 ) ( x + 2 ) 2 . Số điểm cực trị của hàm số đã cho là:
A. 2
B. 1
C. 4
D. 3
Cho hàm số
F
(
x
)
a
x
3
+
b
x
2
+
c
x
+
1
là một nguyên hàm của hàm số f(x) thỏa mãn f(1) 2, f(2) 3, f(3) 4. Hàm số F(x) là
Đọc tiếp
Cho hàm số F ( x ) = a x 3 + b x 2 + c x + 1 là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là
