Biểu thức nào sau đây là đúng:
A. q = I t
B. I = t q
C. q = I t
D. I = q t
Công thức nào sau đây mô tả đúng nguyên lí I của NĐLH ?
A. ∆ U = A - Q. B. ∆ U = Q-A.
C. A = ∆ U - Q. D. ∆ U = A + Q.
Đặt một hiệu điện thế U vào hai đầu của một điện trở R thì cường độ dòng điện chạy qua là I. Công thức nào dưới đây không phải là công thức tính nhiệt lượng tỏa ra trên dây dẫn trong thời gian t?
A. Q = U t / I
B. Q = U I t
C. Q = U t 2 / R
D. Q = I 2 R t
Bài 1: Tìm Min của các biểu thức sau:
a) \(B=|x-1|+|x-2|+|x-8|\)
b) \(D=\frac{2x^2-9}{x^2+4}\)
Bài 2: Tìm Max của biểu thức sau:
\(B=\frac{2-5x^2}{4x^2+7}\)
Bài 3:
a)Cho \(x^2+y^2=1\) Hãy tính giá trị của đa thức \(M=2x^4+3x^2y^2++y^4+y^2\)
b) Cho \(x^2+y^2+1=0\) Tính giá trị của biểu thức \(M=x^3+2x^2+x^2y+xy+2x+y+4\)
Mn giúp mk nka! IU nhìu nhắm!
Bài 1: CMR các biểu thức sau luôn dương với mọi giá trị của biểu thức
2x\(^2\)+2x+1
Bài 2: Tìm GTNN của biểu thức
a. A=x\(^2\)-3x+5
b. B=(2x-1)\(^2\) +(x+2)\(^2\)
Bài 3: Tìm GTLN của biểu thức
a. A=4-\(x^2\)+2x
b. B=4x-x\(^2\)
Bài 1:
\(2x^2+2x+1=2\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{1}{2}=2\left(x+\dfrac{1}{2}\right)^2+\dfrac{1}{2}>0\Rightarrowđpcm\)Bài 2:
\(A=x^2-3x+5=\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{11}{4}=\left(x-\dfrac{3}{2}\right)^2+\dfrac{11}{4}\)Với mọi giá trị của x ta có:
\(\left(x-\dfrac{3}{2}\right)^2\ge0\Rightarrow\left(x-\dfrac{3}{2}\right)^2+\dfrac{11}{4}\ge\dfrac{11}{4}\)
Vậy GTNN của A là \(\dfrac{11}{4}\)
Để \(A=\dfrac{11}{4}\) thì \(x-\dfrac{3}{2}=0\Rightarrow x=\dfrac{3}{2}\)
b, \(B=\left(2x-1\right)^2+\left(x+2\right)^2=4x^2-4x+1+x^2+4x+4=5x^2+5=5\left(x^2+1\right)\)
Với mọi giá trị của x ta có:
\(x^2\ge0\Rightarrow x^2+1\ge1\Rightarrow5\left(x^2+1\right)\ge5\)
Vậy \(Min_B=5\)
Để B = 5 thì \(x^2=0\Rightarrow x=0\)
Bài 3:
\(A=4-x^2+2x=-\left(x^2-2x+1\right)+5=-\left(x-1\right)^2+5\)
Với mọi giá trị của x ta có:
\(\left(x-1\right)^2\ge0\Rightarrow-\left(x-1\right)^2\le0\Rightarrow-\left(x-1\right)^2+5\le5\)Vậy \(Max_A=5\)
Để A = 5 thì \(x-1=0\Rightarrow x=1\)
b, \(B=4x-x^2=4-\left(4-4x+x^2\right)=4-\left(2-x\right)^2\)
Với mọi giá trị của x ta có :
\(\left(2-x\right)^2\ge0\Rightarrow4-\left(2-x\right)^2\le4\)
Vậy \(Max_B=4\)
Để B = 4 thì \(2-x=0\Rightarrow x=2\)
Bài 1: CMR các biểu thức sau luôn dương với mọi giá trị của biểu thức
\(2x^2+2x+1\)
Ta có: \(2x^2>2x\forall x\) mà \(2x^2\ge0\)
\(\Rightarrow2x^2-2x\ge0\)
Vậy \(2x^2+2x+1\ge1\) (đpcm)
bài 1: Tìm GTNN của các biểu thức sau:
a) \(A=x^{2^{ }}-3x+4\)
b) \(B=2x^2-4x+1\)
c) \(C=4x^{2^{ }}-4x\)
Bài 2: Tìm GTLN của các biểu thức sau:
a) \(A=-x-4x+2\)
b) \(B=\left(x+4\right)\left(2-x\right)\)
Bài 3: Tính giá trị của các biểu thức sau:
a) \(A=9x^2+42x+49\) với \(x=1\)
b) \(B=\left(x+y\right)^3-x^{2^{ }}+2xy-y^2\) với \(x-y=-5\)
Bài 3:
a) A = 9x2 + 42x + 49
= (3x + 7)2 (1)
Thay x = 1 vào (1)
Ta có: (3.1 + 7)2
= 102
= 100
Bài 1:
a) C = 4x2 - 4x
= [(2x)2 - 2.2x.1 + 1] - 1
= (2x - 1)2 - 1
Ta có: (2x - 1)2 ≥ 0 với ∀x
Nên: (2x - 1)2 - 1 ≥ -1 với ∀x
Dấu "=" xảy ra ⇔ (2x - 1)2 = 0
2x - 1 = 0
2x = 1
x = \(\frac{1}{2}\)
Vậy GTNN của biểu thức C là -1 khi x = \(\frac{1}{2}\)
Bài 2:
b) B = (x + 4)(2 - x)
= 2x - x2 + 8 - 4x
= -x2 - 2x + 8
= -(x2 + 2x + 1 - 1) + 8
= -(x + 1)2 + 9
Ta có: -(x + 1)2 ≤ 0 với ∀x
Nên: -(x + 1)2 + 9 ≤ 9 với ∀x
Dấu "=" xảy ra ⇔ -(x + 1)2 = 0
x + 1 = 0
x = -1
Vậy GTLN của biểu thức B là 9 khi x = -1
Bạn ơi bài 2a có đúng đề bài không vậy bạn?![]()
Bạn ơi câu 2a thiếu mũ 2 ở x nha :3
Bài 2:
a) A = -x2 - 4x + 2
= -(x2 + 4x + 2 - 2) + 2
= -(x + 2)2 + 4
Ta có: -(x + 2)2 ≤ 0 với ∀x
Nên: -(x + 2)2 + 4 ≤ 4 với ∀x
Dấu "=" xảy ra ⇔ -(x + 2)2 = 0
x + 2 = 0
x = -2
Vậy GTLN của biểu thức A là 4 khi x = -2
Sự biến thiên theo thời gian của điện tích q của một bản tụ điện và của cường độ dòng điện i trong một mạch dao động lí tưởng được biểu diễn bằng đố thị q(t) nét liền và i(t) nét đứt trên cùng một hệ tọa độ [(q,i)t] ở Hình 20.3. Đồ thị nào đúng ? Lấy mốc thời gian là lúc tụ điện bắt đầu phóng điện trong mạch.
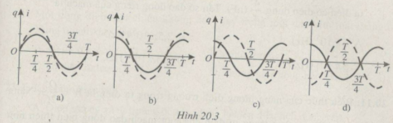
A. Đồ thị a. B. Đồ thị b.
C. Đồ thị c. D. Không có đồ thị nào.
Câu 18 . Phát biểu nào sau đây là sai ?
A. \(\sqrt{2}\) ∈ I B. \(\sqrt{9}\) ∈ I C. π ∈ I D. \(\sqrt{4}\) ∈ Q
Bài 1: Tìm x biết:
a) \(|x-1|=x-1\)
b) \(|2x-3|=3-2x\)
c) \(|2x-3|-x=5\)
d) \(|x|-x=6\)
Bài 2: a) Tìm GTLN của biểu thức sau:
A=\(5-|2x-1|\)
B=\(-|x+5|-2017\)
b) Tìm GTNN của biểu thức sau:
C=\(5+|x-3|\)
D=\(|x-2016|+2017\)
a) |x - 1| = x - 1
Vậy x là 1 số tự nhiên.
1. a.|x - 1 |= x -1
\(\left[{}\begin{matrix}x-1=x-1\\x-1=-x+1\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\2x=2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Chúc bạn học tốt !
Bài 1:
a) \(\left|x-1\right|=x-1\)
\(\Rightarrow\left[{}\begin{matrix}x-1=x-1\\x-1=-x+1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\in\varnothing\\2x=2\Rightarrow x=1\end{matrix}\right.\)
b) \(\left|2x-3\right|=3-2x\)
\(\Rightarrow\left[{}\begin{matrix}2x-3=3-2x\\2x-3=-3+2x\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}4x=6\\x\in\varnothing\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1,5\\x\in\varnothing\end{matrix}\right.\)
c) \(\left|2x-3\right|-x=5\)
\(\Rightarrow\)\(\left|2x-3\right|=5+x\)
\(\Rightarrow\)\(\left[{}\begin{matrix}2x-3=5+x\\2x-3=-5-x\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=8\\3x=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=\dfrac{-2}{3}\end{matrix}\right.\)
Bài 2:
a) \(A=5-\left|2x-1\right|\)
Xét \(\left|2x-1\right|\ge0\)
\(\Rightarrow5-\left|2x-1\right|\le5\)
\(\Rightarrow Max_A=5\Leftrightarrow2x-1=0\)
\(\Leftrightarrow x=\dfrac{1}{2}\)
\(B=-\left|x+5\right|-2017\)
Xét \(-\left|x+5\right|\le0\)
\(\Rightarrow-\left|x+5\right|-2017\le-2017\)
\(\Rightarrow Max_B=-2017\Leftrightarrow\left|x+5\right|=0\)
\(\Leftrightarrow x=-5\)
b) \(C=5+\left|x-3\right|\)
Xét \(\left|x-3\right|\ge0\)
\(\Rightarrow5+\left|x-3\right|\ge5\)
\(\Rightarrow Min_C=5\Leftrightarrow x-3=0\)
\(\Rightarrow x=3\)
\(D=\left|x-2016\right|+2017\)
Xét \(\left|x-2016\right|\ge0\)
\(\Rightarrow\left|x-2016\right|+2017\ge2017\)
\(\Rightarrow Min_D=2017\Leftrightarrow x-2016=0\)
\(\Rightarrow x=2016\)
Cho biểu thức sau:
A=(\(\dfrac{x-2}{2x-2}\)\(+\)\(\dfrac{3}{2x-2}\)\(-\)\(\dfrac{x+3}{2x+2}\)):(1-\(\dfrac{x-3}{x+1}\))
a)Tìm điều kiện và rút gọn
b)Tính giá trị của biểu thức khi x=2005
c)Tìm x để A có giá trị=-1002
GIẢI GIÚP MÌNH BÀI NÀY VỚI !!!!!!!!
Cho biểu thức \(Q=\left(\frac{1}{x+1}+\frac{6x+3}{x^3+1}-\frac{2}{x^2-x+1}\right):\left(x+2\right)\)
a)Tìm điều kiện xác định của Q , rút gọn Q .
b)Tìm x khi Q=\(\frac{1}{3}\).
c)Tìm giá trị lớn nhất của biểu thức Q .
Quan trọng là giải giúp mình câu c nha!!!!!!Cảm ơn!!!!!
c/\(Q=\frac{1}{x^2-x+1}\)
Ta có \(x^2-x+1=\left(x^2-x+\frac{1}{4}\right)+\frac{3}{4}=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Suy ra MAX Q=3/4 với x=1/2