Cho phương trình z 2 - 4 z 2 - 3 z 2 - 4 z - 40 = 0 . Gọi z 1 ; z 2 ; z 3 và z 4 là bốn nghiệm của phương trình đã cho. Tính giá trị của biểu thức P = z 1 2 + z 2 2 + z 3 3 + z 4 2
A. 33
B. 34.
C. 35
D. 36
Giải phương trình:
\(\left(\dfrac{z^2+2z+4}{z-2}\right)^2+7=\dfrac{8-z^3}{\left(z-2\right)^2}\)
ĐKXĐ: \(z\ne2\)
\(\left(\dfrac{z^2+2z+4}{z-2}\right)^2+7+\dfrac{\left(z-2\right)\left(z^2+2x+4\right)}{\left(z-2\right)^2}=0\)
\(\Leftrightarrow\left(\dfrac{z^2+2z+4}{z-2}\right)^2+\dfrac{z^2-2z+4}{z-2}+7=0\)
Đặt \(\dfrac{z^2+2z+4}{z-2}=x\)
\(\Rightarrow x^2+x+7=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{27}{4}=0\)
Pt đã cho vô nghiệm
Số nghiệm phức của phương trình z + 2 | z | + 3 - i = ( 4 + i ) | z | z là
A. 1.
B. 2.
C. 3.
D. 4.
Tìm a,b sao cho hệ phương trình có nghiệm duy nhất
xyz+z=a
xyz^2+z=b
x^2+y^2+z^2=4
Giúp mk giải bài này vs @@ . Ai giải chi tiết mk sẽ tick cho <3 <3
Cho phương trình: ( z2 - z) ( z + 3) (z + 2) = 10 .Tính tổng tất cả các phần thực của các nghiệm phương trình trên.
A. -1
B. -2
C. -3
D. -4
Chọn D.
Phương trình đã cho tương đương với phương trình
z( z + 2) ( z - 1) ( z + 3)
Hay ( z2 + 2z) ( z2 + 2z - 3) = 10
Đặt t = z2 + 2z. Khi đó phương trình trở thành: t2 - 2t – 10 = 0.
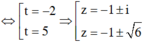
Vậy phương trình có các nghiệm: ![]()
Tổng tất cả các phần thực của các nghiệm phương trình đã cho là:
-1+ ( -1) + (-1) + ( -1) = -4.
cho x, y, z là nghiệm bất phương trình \(\left\{{}\begin{matrix}x^2+y^2+z^2=8\\xy+yz+zx=4\end{matrix}\right.\)
Chứng minh rằng \(-\dfrac{8}{3}\) ≤ x, y, z ≤ \(\dfrac{8}{3}\)
Trong không gian tọa độ Oxyz, cho mặt cầu (S) có phương trình (x-2)2 + (y+1)2 + (z-3)2 = 20. Mặt phẳng có phương trình x-2y+2z-1=0 và đường thẳng ∆ có phương trình x 1 = y + 2 2 = z + 4 - 30 . Viết phương trình đường thẳng ∆ ' nằm trong mặt phẳng α vuông góc với ∆ đồng thời cắt (S) theo một dây cung có độ dài lớn nhất.
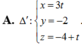

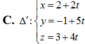
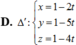
Giải các phương trình sau: ( z2 + z) 2 + 4( z2+ z) - 12 = 0
A. z = -1; z = 2
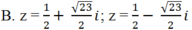
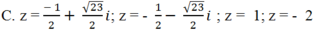
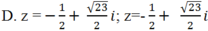
Chọn C.
Đặt t = z2 + z; Phương trình đã cho trở thành
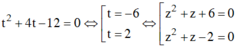
Với 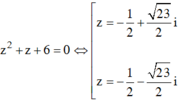
Với 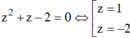
Vậy phương trình đã cho có 4 nghiệm.
giải hệ phương trình sau
\(\left\{{}\begin{matrix}x+\sqrt{y-2}+\sqrt{4-z}=y^2-5z+11\\y+\sqrt{z-2}+\sqrt{4-x}=z^2-5x+11\\z+\sqrt{x-2}+\sqrt{4-y}=x^2-5y+11\end{matrix}\right.\)
ĐKXĐ : \(2\le x,y,z\le4\)
Từ hệ phương trình ta suy ra được
\(\Sigma x+\Sigma\sqrt{x-2}+\Sigma\sqrt{4-x}=\Sigma x^2-5\Sigma x+33\\ \Leftrightarrow\Sigma\left(x^2-6x+9\right)+6=\Sigma\left(\sqrt{x-2}+\sqrt{4-x}\right)\\ \Leftrightarrow\Sigma\left(x-3\right)^2+6=\Sigma\left(\sqrt{x-2}+\sqrt{4-x}\right)\left(1\right)\)
Áp dụng bất đẳng thức \(\sqrt{A}+\sqrt{B}\le\sqrt{2\left(A+B\right)}\)
\(\Sigma\left(\sqrt{x-2}+\sqrt{4-x}\right)\le\Sigma\sqrt{2\left(x-2+4-x\right)}=\Sigma2=6\)
\(\Rightarrow\Sigma\left(x-3\right)^2+6\le6\Rightarrow\Sigma\left(x-3\right)^2\le0\)
Mà \(\Sigma\left(x-3\right)^2\ge0\)
\(\Rightarrow\left(x-3\right)^2=\left(y-3\right)^2=\left(z-3\right)^2=0\\ \Leftrightarrow x=y=z=3\)
Thay vào ta thấy thỏa mãn -> x=y=z=3 là nghiệm hpt
Giải phương trình:
\(x+y+z+11=2\sqrt{x}+4\sqrt{y-1}+6\sqrt{z-2}\)
Lời giải:
ĐKXĐ: $x\geq 0; y\geq 1; z\geq 2$
PT \(\Leftrightarrow (x-2\sqrt{x}+1)+[(y-1)-4\sqrt{y-1}+4]+[(z-2)-6\sqrt{z-2}+9]=0\)
\(\Leftrightarrow (\sqrt{x}-1)^2+(\sqrt{y-1}-2)^2+(\sqrt{z-2}-3)^2=0\)
Vì \((\sqrt{x}-1)^2, (\sqrt{y-1}-2)^2, (\sqrt{z-2}-3)^2\geq 0\) nên để tổng của chúng bằng $0$ thì:
\((\sqrt{x}-1)^2=(\sqrt{y-1}-2)^2=(\sqrt{z-2}-3)^2=0\)
$\Leftrightarrow x=1; y=5; z=11$