xác định và ghi tọa độ địa l1 của các điểm A,B,C

Những câu hỏi liên quan
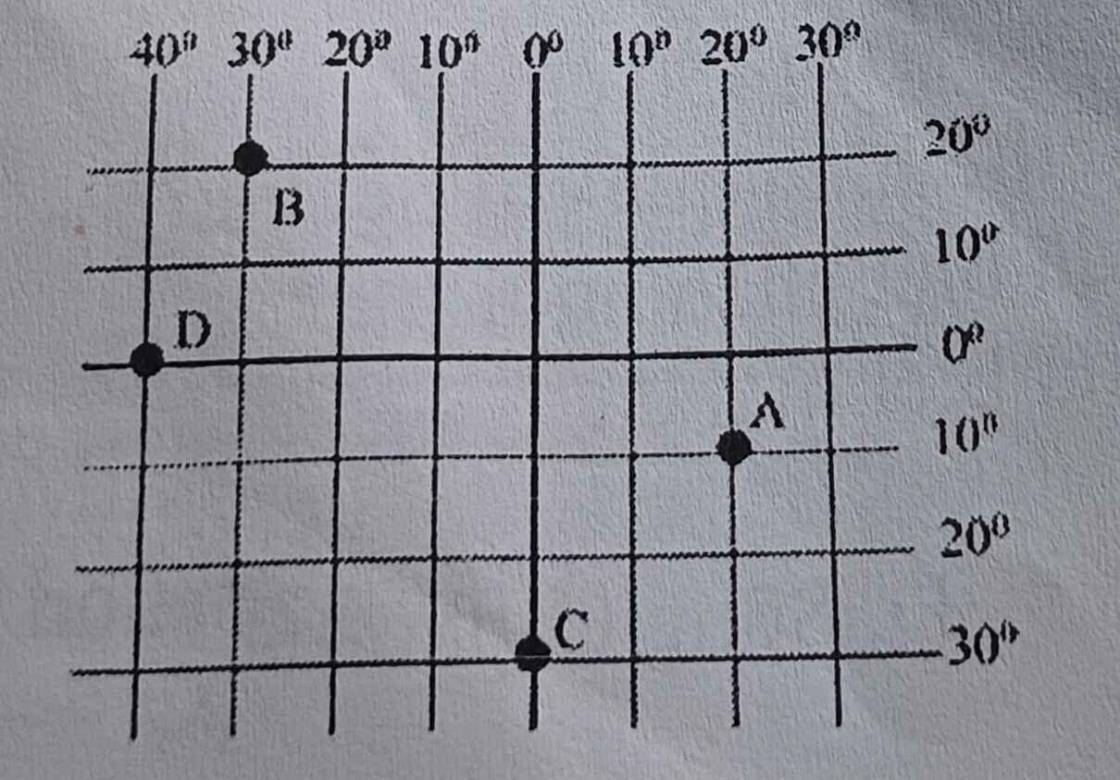 Xác định tọa độ địa lí của các điểm A, B, C, D.
Xác định tọa độ địa lí của các điểm A, B, C, D.
A:20oĐ và 10oN
B:30oT và 20oB
C:0o và 30oN
D:40oT và 0o
Đúng 0
Bình luận (0)
Quan sát hình 1.2, hãy xác định tọa độ địa lí của các điểm A, B, C, D.
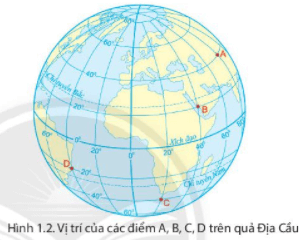
Vị trí A: 40oB, 80oĐ.
Vị trí B: 20oB, 40oĐ.
Vị trí C: 40oN, 20oĐ.
Vị trí D: 20oN, 40oT.
Đúng 5
Bình luận (3)
Hãy xác định tọa độ địa lí của các điểm A, B, C, D, E trong hình dưới đây
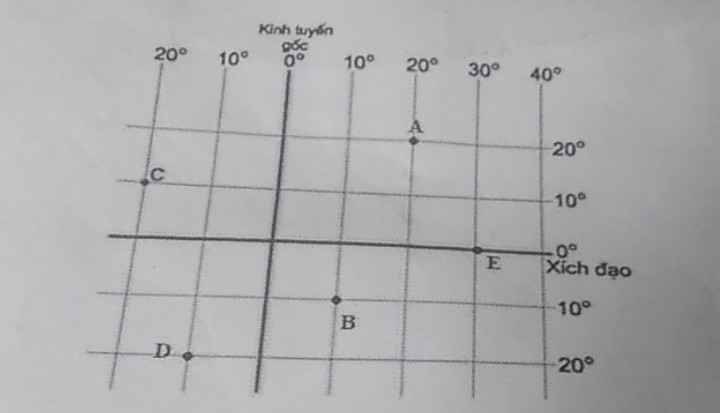
- A (20oB, 20oĐ)
- B (10oĐ, 10oN)
- C (20oT, 10oB)
- D (10oT, 20oN)
- E (30oĐ, 0o)
Đúng 2
Bình luận (0)
- A (20oB, 20oĐ)
- B (10oĐ, 10oN)
- C (20oT, 10oB)
- D (10oT, 20oN)
- E (30oĐ, 0o)
Đúng 0
Bình luận (0)
Cách xác định và ghi tọa độ địa lí của 1 điểm.Cách xác định phương hướng trên bản đồ
Tham khảo:
– Kinh độ: Kinh độ của một điểm là khoảng cách tính bằng số đo từ kinh tuyến đi qua điểm đó đến kinh tuyến gốc
– Vĩ độ: Vĩ độ địa lý của một điểm là góc hợp bởi đường dây dọi đi qua điểm đó và mặt phẳng xích đạo.
– Tọa độ địa lí của 1 điểm là kinh độ và vĩ độ của điểm đó.
Xác định kinh độ vĩ độ trên bản đồ
Trên mỗi tấm bản đồ đều được in các đường kinh độ và vĩ độ, dựa vào đó ta có thể xác định được tọa độ địa lý, và cách xác định tọa độ 1 điểm trên bản đồ như sau:
Viết:
Kinh độ trênVĩ độ dưới
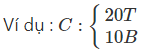
- Theo quy ước trên bản đồ địa lý, khi bạn nhiền vào bản đồ thì phía nam ở bên dưới, phía bắc ở bên trên, phía đông bên tay phải, phía tây bên tay trái (trên bắc – dưới nam – phải đông – trái tây). Khi đã xác định được một hướng thì bạn hoàn toàn có thể xác định được các hướng còn lại trên bản đồ một cách dễ dàng.
Đúng 1
Bình luận (0)
Dựa vào kinh,vĩ tuyến
Hướng chỉ đầu Bắc
A(Vĩ tuyến,Kinh tuyến)
Đúng 0
Bình luận (0)
Câu 1: Trình bày khái niệm kinh, vĩ tuyến và đặc điểm của các đường kinh, vĩ tuyến? Cách tính số lượng các đường kinh, vĩ tuyến trên quả Địa Cầu và xác định tọa độ địa lí của một điểm trên bản đồ?Câu 2: Trình bày các cách xác định phương hướng trên bản đồ?Câu 3: Nêu khái niệm và ý nghĩa của tỉ lệ bản đồ? Tính khoảng cách trên thực tế và khoảng cách trên bản đồ dựa vào tỉ lệ bản đồ?Câu 4: Trình bày đặc điểm hình dạng, kích thước của Trái Đất?Câu 5: Trình bày đặc điểm của chuyển động tự quay quanh...
Đọc tiếp
Câu 1: Trình bày khái niệm kinh, vĩ tuyến và đặc điểm của các đường kinh, vĩ tuyến? Cách tính số lượng các đường kinh, vĩ tuyến trên quả Địa Cầu và xác định tọa độ địa lí của một điểm trên bản đồ?
Câu 2: Trình bày các cách xác định phương hướng trên bản đồ?
Câu 3: Nêu khái niệm và ý nghĩa của tỉ lệ bản đồ? Tính khoảng cách trên thực tế và khoảng cách trên bản đồ dựa vào tỉ lệ bản đồ?
Câu 4: Trình bày đặc điểm hình dạng, kích thước của Trái Đất?
Câu 5: Trình bày đặc điểm của chuyển động tự quay quanh trục của Trái Đất và các hệ quả? Giải thích một số hiện tượng thực tế sinh ra do sự vận động tự quay quanh trục của Trái Đất?
Câu 6: Tính giờ của các khu vực khác nhau trên Trái Đất theo giờ quốc tế(GMT) ?
Câu 7: Trình bày sự chuyển động của Trái Đất quanh Mặt Trời và các hệ quả? Giải thích một số hiện tượng thực tế sinh ra do sự chuyển động của Trái Đất quanh Mặt Trời?
2) Dựa vào các đường kinh tuyến, vĩ tuyến
- Dựa vào mũi tên chỉ hướng Bắc sau đó xác định các hướng còn lại
Đúng 1
Bình luận (9)
3) https://hoc24.vn/ly-thuyet/bai-3-ti-le-ban-do-khai-niem-ban-do.1337/
chắc là cái câu này =))
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4).a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox. b) Xác định các hệ số a và b biết đồ thị hàm số y ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút).c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ n...
Đọc tiếp
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4).
a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y = 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox.
b) Xác định các hệ số a và b biết đồ thị hàm số y= ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút).
c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ nhất).
a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
Vậy: (d): y=2x+b
Vì (d) đi qua điểm C(-1;4) nên
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
hay b=6
Vậy: (d): y=2x+6
Thay y=0 vào (d), ta được:
2x+6=0
hay x=-3
Vậy: A(-3;0)
b) Vì y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\b=a+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=\dfrac{-4}{5}+4=\dfrac{-4}{5}+\dfrac{20}{5}=\dfrac{16}{5}\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4). a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox. b) Xác định các hệ số a và b biết đồ thị hàm số y ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút). c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ...
Đọc tiếp
Trên mặt phẳng tọa độ cho hai điểm B(4; 0) và C(-1; 4).
a) Viết phương trình đường thẳng (d) đi qua điểm C và song song với đường thẳng y = 2x-3. Xác định tọa độ giao điểm A của đường thẳng (d) với trục hoành Ox.
b) Xác định các hệ số a và b biết đồ thị hàm số y= ax +b đi qua 2 điểm B và C. Tính góc tạo bởi đường thẳng BC và trục hoành Ox (làm tròn đến phút).
c) Tính chu vi của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimét) (kết quả làm tròn đến chữ số thập phân thứ nhất).
a) Gọi (d): y=ax+b
Vì (d)//y=2x-3 nên ta có: \(\left\{{}\begin{matrix}a=2\\b\ne-3\end{matrix}\right.\)
=> (d): y=2x+b
Thay x=-1 và y=4 vào (d), ta được:
\(2\cdot\left(-1\right)+b=4\)
\(\Leftrightarrow b=6\)
Vậy: (D): y=2x+6
Thay y=0 vào (d),ta được:
\(2x+6=0\)
\(\Leftrightarrow x=-3\)
Vậy: A(-3;0)
b) Vì đồ thị hàm số y=ax+b đi qua hai điểm B(4;0) và C(-1;4) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=0\\-a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a=-4\\-a+b=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{4}{5}\\b=4+a=4+\dfrac{-4}{5}=4-\dfrac{4}{5}=\dfrac{16}{5}\end{matrix}\right.\)
Vậy: \(a=-\dfrac{4}{5}\); \(b=\dfrac{16}{5}\)
c) Độ dài đoạn thẳng AB là:
\(AB=\sqrt{\left(-3-4\right)^2+\left(0-0\right)^2}=7\)(cm)
Độ dài đoạn thẳng AC là:
\(AC=\sqrt{\left(-3+1\right)^2+\left(0-4\right)^2}=2\sqrt{5}\left(cm\right)\)
Độ dài đoạn thẳng BC là:
\(BC=\sqrt{\left(4+1\right)^2+\left(0-4\right)^2}=\sqrt{41}\left(cm\right)\)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC\)
\(=7+2\sqrt{5}+\sqrt{41}\)
\(\simeq17,9\left(cm\right)\)
Đúng 1
Bình luận (1)
(Làm hộ mình câu b nha)
Cho các hàm số: \(y=x^2\) và y=-x+2.
a)Xác định tọa độ các giao điểm A, B của đồ thị hai hàm số đã cho và tọa độ trung điểm I của AB
b) Xác định tọa độ của điểm M thuộc DTHS: \(y=x^2\) sao cho tam giác ABM cân tại M
b: A(1;1) B(-2;4)
\(M\left(x;x^2\right)\)
Theo đề, ta có: MA=MB
\(\Leftrightarrow\sqrt{\left(x-1\right)^2+\left(x^2-1\right)^2}=\sqrt{\left(x+2\right)^2+\left(x^2-4\right)^2}\)
\(\Leftrightarrow x^2-2x+1+x^4-2x^2+1=x^2+4x+4+x^4-8x^2+16\)
\(\Leftrightarrow6x^2-6x-18=0\)
\(\Leftrightarrow x^2-x-3=0\)
\(\Delta=\left(-1\right)^2-4\cdot1\cdot\left(-3\right)=13>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{1-\sqrt{13}}{2}\\x_2=\dfrac{1+\sqrt{13}}{2}\end{matrix}\right.\)
Vậy: \(M\left(\dfrac{1-\sqrt{13}}{2};\dfrac{7-\sqrt{13}}{2}\right);M\left(\dfrac{1+\sqrt{13}}{2};\dfrac{7+\sqrt{13}}{2}\right)\)
Đúng 2
Bình luận (0)
Hãy ghi tọa độ địa lí của các điểm A, B, C trên bản đồ hình 12.

























