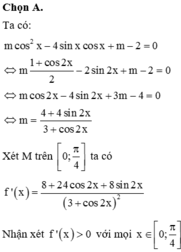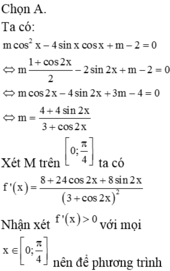\(\Leftrightarrow m\left(2cos^2x-1\right)-4\left(m-2\right)cosx+3m-6=0\)

\(\Leftrightarrow m.cos^2x-2\left(m-2\right)cosx+m-3=0\)

Đặt \(cosx=t\Rightarrow0\le t< 1\)

\(\Rightarrow f\left(t\right)=mt^2-2\left(m-2\right)t+m-3=0\) (1)

Ứng với mỗi giá trị \(t\in\left(0;1\right)\) có 2 giá trị x thuộc \(\left(-\frac{\pi}{2};\frac{\pi}{2}\right)\) thỏa mãn (t=0 thì có đúng 1 giá trị x nên ko phù hợp)

Vậy pt đã cho có đúng 2 nghiệm thuộc \(\left(-\frac{\pi}{2};\frac{\pi}{2}\right)\) khi và chỉ khi (1) có đúng 1 nghiệm thuộc \(\left(0;1\right)\) và ko có nghiệm bằng 0

- Với \(m=0\Rightarrow t=\frac{3}{4}\) (thỏa mãn)

- Với \(m\ne0\) để pt có nghiệm khác 0 \(\Rightarrow m\ne3\)

\(\Delta'=\left(m-2\right)^2-m\left(m-3\right)=-m+4\)

TH1: \(\left\{{}\begin{matrix}\Delta'=0\\-\frac{b}{2a}=\frac{m-2}{m}\in\left(0;1\right)\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=4\\\frac{m-2}{m}\in\left(0;1\right)\end{matrix}\right.\) (thỏa mãn)

TH2: \(\Delta'>0\Rightarrow m< 4\)

Pt có đúng 1 nghiệm thuộc \(\left(0;1\right)\) khi \(f\left(0\right).f\left(1\right)< 0\)

\(\Leftrightarrow\left(m-3\right)\left(m-2m+4+m-3\right)< 0\) \(\Rightarrow m< 3\)

Vậy \(\left[{}\begin{matrix}m=4\\m< 3\end{matrix}\right.\)

1. Để biết tại sao \(0\le cosx< 1\) thì bạn cần vẽ đường tròn lượng giác để xác định

2. Bạn thay \(t=0\) vào (1) thành \(m-3\ne0\) thôi

Đặt \(cosx=t\in\left[-1;1\right]\)

\(\Rightarrow6t^2+\left(9m-7\right)t-6m+2=0\)

\(\Leftrightarrow6t^2-7t+2+9mt-6m=0\)

\(\Leftrightarrow\left(2t-1\right)\left(3t-2\right)+3m\left(3t-2\right)=0\)

\(\Leftrightarrow\left(3t-2\right)\left(2t+3m-1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}cosx=\dfrac{2}{3}\\cosx=\dfrac{-3m+1}{2}\end{matrix}\right.\) 

(Chà tới đây mới thấy ko cần đặt ẩn phụ, nhìn con số 9m và 6m to 1 cách vô lý đã nghi nghi có gì đó bất thường trong nghiệm :D)

Pt \(cosx=\dfrac{2}{3}\) cho 1 nghiệm thuộc \(\left(0;\dfrac{\pi}{2}\right)\)

Để pt có 3 nghiệm pb thì \(cosx=\dfrac{-3m+1}{2}\) cho 2 nghiệm pb thuộc khoảng đã cho

Từ đường tròn lượng giác ta dễ dàng suy ra: \(-1< \dfrac{-2m+1}{2}< 0\)

\(\Leftrightarrow\left(cosx+1\right)\left(4cos2x-m.cosx\right)=m\left(1-cosx\right)\left(1+cosx\right)\)

\(\Leftrightarrow4cos2x-m.cosx=m\left(1-cosx\right)\)

\(\Leftrightarrow4cos2x=m\)

\(\Rightarrow cos2x=\dfrac{m}{4}\)

Pt có đúng 2 nghiệm thuộc đoạn đã cho khi và chỉ khi:

\(-1< \dfrac{m}{4}\le-\dfrac{1}{2}\Leftrightarrow-4< m\le-2\)

Có 2 giá trị nguyên của m thỏa mãn

1.

\(3cos2x-7=2m\)

\(\Leftrightarrow cos2x=\dfrac{2m-7}{3}\)

Phương trình đã cho có nghiệm khi:

\(-1\le\dfrac{2m-7}{3}\le1\)

\(\Leftrightarrow2\le m\le5\)

2.

\(2cos^2x-\sqrt{3}cosx=0\)

\(\Leftrightarrow cosx\left(2cosx-\sqrt{3}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\cosx=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k\pi\\x=\pm\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Rightarrow\) Có 4 nghiệm \(\dfrac{\pi}{2};\dfrac{3\pi}{2};\dfrac{\pi}{6};\dfrac{11\pi}{6}\) thuộc đoạn \(\left[0;2\pi\right]\)