Đường thẳng d1 đi qua 2 điểm \(A\left(-4;0\right)\) và \(B\left(0;2\right)\). Đg thg d2 là ảnh của d1 qua phép tịnh tiến \(\overrightarrow{u}\left(0;3\right)\). Tìm phương trình của d2

Những câu hỏi liên quan
Cho 2 đường thẳng
d1 : \(\left\{{}\begin{matrix}x=4-3t\\y=-1+2t\end{matrix}\right.\) và d2 : x+2y-1=0
a.Tìm tọa độ giao điểm A của d1 và d2
b. Viết ptts và pttq của:
- Đường thẳng đi qua A và vuông góc với d1
- Đường thẳng đi qua A và song song với d2
a. Tọa độ A thỏa mãn:
\(4-3t+2\left(-1+2t\right)-1=0\Rightarrow t=-1\)
\(\Rightarrow A\left(7;-3\right)\)
b. d1 nhận \(\left(-3;2\right)=-1\left(3;-2\right)\) là 1 vtcp nên đường thẳng d nhận \(\left(2;3\right)\) là 1 vtcp và \(\left(3;-2\right)\) là 1 vtpt
Phương trình tham số d: \(\left\{{}\begin{matrix}x=7+2t\\y=-3+3t\end{matrix}\right.\)
Pt tổng quát:
\(3\left(x-7\right)-2\left(y+3\right)=0\Leftrightarrow3x-2y-27=0\)
Đường thẳng d2 nhận \(\left(1;2\right)\) là 1 vtpt nên d3 nhận \(\left(1;2\right)\) là 1 vtpt và \(\left(2;-1\right)\) là 1 vtcp
Phương trình tham số d3: \(\left\{{}\begin{matrix}x=7+2t\\y=-3-t\end{matrix}\right.\)
Pt tổng quát:
\(1\left(x-7\right)+2\left(y+3\right)=0\Leftrightarrow x+2y-1=0\)
Đúng 0
Bình luận (0)
Viết phương trình đường thẳng (d)
A, (d) đi qua m (-2;5) là vuông góc với (d1) y=(-1 )/2x+2
B, (d) song song đường thẳng (d1) y=-3+4 và đi qua giao điểm của 2 đường thẳng (d2) y=2x-3 và (d3) y=3x-7/2
a: (d) vuông góc (d1)
=>a*(-1/2)=-1
=>a=2
=>(d): y=2x+b
Thay x=-2 và y=5 vào (d), ta được:
b-4=5
=>b=9
b:
Sửa đề: (d1): y=-3x+4
Tọa độ giao của (d2) và (d3) là:
3x-7/2=2x-3 và y=2x-3
=>x=1/2 và y=1-3=-2
(d)//(d1)
=>(d): y=-3x+b
Thay x=1/2 và y=-2 vào (d), ta được:
b-3/2=-2
=>b=1/2
=>y=-3x+1/2
Đúng 1
Bình luận (1)
Bài 6: Cho điểm A(-2;2) và đường thẳng (:y = -2(x+1)
1. Điểm A có thuộc (d1) không ? Vì sao ?
2. Tìm a để hàm số (P): \(y=x^2\) đi qua A
3. Xác định Phương trình đường thẳng (d2) đi qua A và vuông góc với (d1)
4. Gọi A và B là giao điểm của (P) và (d2) ; C là giao điểm của (d1) với trục tung . Tìm toạ độ của B và C . Tính chu vi tam giác ABC?
1) Thay x=-2 và y=2 vào hàm số y=-2(x+1), ta được:
\(-2\cdot\left(-2+1\right)=\left(-2\right)\cdot\left(-1\right)=2=y\)
Vậy: A(-2;2) thuộc (d1)
Đúng 1
Bình luận (0)
cho đường thẳng(d1) y=x+2 gọi A là điểm thuộc đường thẳng (d1) có hoành độ x=2 viết phương trình đường thẳng (d2) đi qua A vuông góc với (d1)
Tọa độ điểm `A` có `x=2` và `in (d_1)`
`=>` Thay `x=2` vào `(d_1)` có: `y=2+2=4`
`=>A(2;4)`
Gọi ptr đường thẳng `(d_2)` có dạng: `y=ax + b`
Vì `(d_2) \bot (d_1)=>a.a'=-1`
`=>a.1=-1<=>a=-1`
Thay `A(2;4)` và `a=-1` vào `(d_2)` có:
`4=-1.2+b<=>b=6`
Vậy ptr đường thẳng `(d_2)` là: `y=-x+6`
Đúng 2
Bình luận (0)
Trong các cách sau, có bao nhiêu cách để xác định một mặt phẳng 1. Đi qua 3 điểm phân biệt 2. Đi qua 1 điểm và chứa 1 đường thẳng không đi qua điểm đó 3. Đi qua 2 đường thẳng bất kì 4. Đi qua đường thẳng (d1) và song song với đường thẳng (d2) cho trước, sao cho d1 và d2 không cắt nhau 5. Song song với 2 đường thẳng cắt nhau 6. Song song với 2 đường thẳng chéo nhau 7. Đi qua 1 điểm và song song với một đường thẳng cho trước 8. Đi qua 1 điểm và song song với một m...
Đọc tiếp
Trong các cách sau, có bao nhiêu cách để xác định một mặt phẳng
1. Đi qua 3 điểm phân biệt
2. Đi qua 1 điểm và chứa 1 đường thẳng không đi qua điểm đó
3. Đi qua 2 đường thẳng bất kì
4. Đi qua đường thẳng (d1) và song song với đường thẳng (d2) cho trước, sao cho d1 và d2 không cắt nhau
5. Song song với 2 đường thẳng cắt nhau
6. Song song với 2 đường thẳng chéo nhau
7. Đi qua 1 điểm và song song với một đường thẳng cho trước
8. Đi qua 1 điểm và song song với một mặt phẳng cho trước
A. 2
B. 3
C. 4
D. 5
Đáp án B
Các cách xác định mặt phẳng đúng: 2; 4 ; 8
1. Đi qua 3 điểm phân biệt không thẳng hàng
3. Trong trường hợp 2 đường thẳng chéo nhau thì không thể xác định được mặt phẳng
5. Song song với 2 đường thẳng cắt nhau Có vô số mặt phẳng như vậy.
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
6. Song song với 2 đường thẳng chéo nhau Có vô số mặt phẳng như vậy
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
7. Đi qua 1 điểm và song song với một đường thẳng cho trước. Có vô số mặt phẳng như vậy
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho điểm A(4;2;-3) và hai đường thẳng
d
1
:
x
4
y
6
z
−
1
,
d
2
:
x...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(4;2;-3) và hai đường thẳng d 1 : x 4 = y 6 = z − 1 , d 2 : x = − 1 + 2 t y = 2 + 3 t z = 4 − t . Đường thẳng d đi qua điểm A, đồng thời vuông góc với hai đường thẳng d 1 , d 2 có phương trình là:
A. x = 3 + 4 t y = − 2 + 2 t z = − 3 − 3 t
B. x = 4 + 2 t y = 2 + 3 t z = − 3 − t
C. x = 4 + 3 t y = 2 + 2 t z = − 3
D. x = 4 + 3 t y = 2 − 2 t z = − 3
Đáp án D
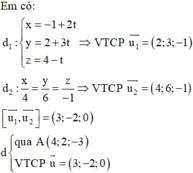
Đường thẳng d đi qua điểm A, đồng thời vuông góc với d 1 , d 2 có phương trình là: x = 4 + 3 t y = 2 − 2 t z = − 3
Đúng 0
Bình luận (0)
(d1):y=-x+4 và (d2):y=x+2
a) vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ giao điểm M của hai đường thẳng (d1) và (d2) xác định đường thẳng (d3) biết (d3) đi qua điểm M
Cho điểm A(1; 1) và hai đường thẳng (
d
1
): y x − 1; (
d
2
): y 4x − 2. Viết phương trình đường thẳng (d) đi qua điểm A và cắt các đường thẳng (d1), (
d
1
) tạo thành một tam giác vuông. A. y 2x–1 B. y –2x+3 C.
y
−
x
+...
Đọc tiếp
Cho điểm A(1; 1) và hai đường thẳng ( d 1 ): y = x − 1; ( d 2 ): y = 4x − 2. Viết phương trình đường thẳng (d) đi qua điểm A và cắt các đường thẳng (d1), ( d 1 ) tạo thành một tam giác vuông.
A. y = 2x–1
B. y = –2x+3
C. y = − x + 2 y = − 1 4 x + 5 4
D. Không xác định được
Tìm giao điểm của 2 đường thẳng
(d1) 5x - 2y = 6 , d1 đi qua A ( 5;-1)
(d2) x + by = 2 , d2 đi qua B (-7;3)
Cho 3 điểm A ( 0; -8 ) , B ( 5/2 ; 2 ) , C ( 1; 7 ) và đường thẳng (d1) có phương trình 3x + 2y = -1
a, Viết phương trình đường thẳng (d2) đi qua hai điểm A và B
b, Viết phương trình đường thẳng (d3) đi qua điểm C và song song với (d1)




















