a: \(VT=\dfrac{cot^2x}{1+cot^2x}\cdot\dfrac{1+tan^2x}{tan^2x}\)

\(=\dfrac{cot^2x}{\dfrac{1}{sin^2x}}\cdot\dfrac{\dfrac{1}{cos^2x}}{tan^2x}\)

\(=\dfrac{cot^2x}{tan^2x}\cdot\dfrac{1}{cos^2x}:\dfrac{1}{sin^2x}\)

\(=\dfrac{cot^2x}{tan^2x}\cdot\dfrac{sin^2x}{cos^2x}\)

\(=cot^2x\)

\(VP=\dfrac{tan^2x+cot^2x}{1+tan^4x}=\dfrac{\dfrac{sin^2x}{cos^2x}+\dfrac{cos^2x}{sin^2x}}{1+\dfrac{sin^4x}{cos^4x}}\)

\(=\dfrac{sin^4x+cos^4x}{sin^2x\cdot cos^2x}:\dfrac{cos^4x+sin^4x}{cos^4x}\)

\(=\dfrac{sin^4x+cos^4x}{sin^2x\cdot cos^2x}\cdot\dfrac{cos^4x}{cos^4x+sin^4x}=\dfrac{cos^2x}{sin^2x}=cot^2x\)

=>VT=VP

b:

\(\dfrac{tan^2x-cos^2x}{sin^2x}+\dfrac{cot^2x-sin^2x}{cos^2x}\)

\(=\dfrac{\left(\dfrac{sinx}{cosx}\right)^2-cos^2x}{sin^2x}+\dfrac{\left(\dfrac{cosx}{sinx}\right)^2-sin^2x}{cos^2x}\)

\(=\dfrac{sin^2x-cos^4x}{cos^2x\cdot sin^2x}+\dfrac{cos^2x-sin^4x}{sin^2x\cdot cos^2x}\)

\(=\dfrac{sin^2x+cos^2x-cos^4x-sin^4x}{cos^2x\cdot sin^2x}\)

\(=\dfrac{1-\left(cos^2x+sin^2x\right)^2+2\cdot cos^2x\cdot sin^2x}{cos^2x\cdot sin^2x}\)

\(=\dfrac{2\cdot cos^2x\cdot sin^2x}{cos^2x\cdot sin^2x}=2\)

\(cos5x.cos3x+sin7x.sinx=\frac{1}{2}cos8x+\frac{1}{2}cos2x-\frac{1}{2}cos8x+\frac{1}{2}cos6x\)

\(=\frac{1}{2}\left(cos6x+cos2x\right)=cos4x.cos2x\)

\(\frac{1-2sin^22x}{1-sin4x}=\frac{cos^22x-sin^22x}{cos^22x+sin^22x-2sin2x.cos2x}\)

\(=\frac{\left(cos2x-sin2x\right)\left(cos2x+sin2x\right)}{\left(cos2x-sin2x\right)^2}=\frac{cos2x+sin2x}{cos2x-sin2x}=\frac{\frac{cos2x}{cos2x}+\frac{sin2x}{cos2x}}{\frac{cos2x}{cos2x}-\frac{sin2x}{cos2x}}=\frac{1+tan2x}{1-tan2x}\)

\(2cosx-3cos\left(\pi-x\right)+5sin\left(4\pi-\frac{\pi}{2}-x\right)+cot\left(\pi+\frac{\pi}{2}-x\right)\)

\(=2cosx+3cosx-5sin\left(\frac{\pi}{2}+x\right)+cot\left(\frac{\pi}{2}-x\right)\)

\(=5cosx-5cosx+tanx=tanx\)

A = 4 ( 2 sinx . cosx )² . cos²2x + cos²4x

A = 4 . sin²2x . cos²2x + cos²4x

A = ( 2 sin2x . cos2x)² + cos²4x

A = sin² 4x + cos²4x  = 1

\(\frac{sin3x+sinx+sin4x}{cos4x+1+cosx+cos3x}=\frac{2sin2x.cosx+2sin2x.cos2x}{2cos^22x+2cos2x.cosx}=\frac{2sin2x\left(cosx+cos2x\right)}{2cos2x\left(cos2x+cosx\right)}=\frac{sin2x}{cos2x}=tan2x\)

\(\frac{sin^22x+2cos\left(2\pi+\pi+2x\right)-2}{-3+4cos2x+cos\left(\pi-4x\right)}=\frac{sin^22x-2cos2x-2}{-3+4cos2x-cos4x}=\frac{4sin^2x.cos^2x-2\left(2cos^2x-1\right)-2}{-3+4\left(1-2sin^2x\right)-\left(1-2sin^22x\right)}\)

\(=\frac{4cos^2x\left(sin^2x-1\right)}{-8sin^2x+2sin^22x}=\frac{2cos^2x.\left(-cos^2x\right)}{-4sin^2x+4sin^2x.cos^2x}=\frac{cos^4x}{2sin^2x\left(1-cos^2x\right)}\)

\(=\frac{cos^4x}{2sin^4x}=\frac{1}{2}cot^4x\)

a/

\(\Leftrightarrow\frac{1}{2}-\frac{1}{2}cos2x+\frac{1}{2}-\frac{1}{2}cos6x-2\left(1-sin^22x\right)=0\)

\(\Leftrightarrow1-\frac{1}{2}\left(cos6x+cos2x\right)-2cos^22x=0\)

\(\Leftrightarrow1-cos4x.cos2x-2cos^22x=0\)

\(\Leftrightarrow2cos^22x-1+cos4x.cos2x=0\)

\(\Leftrightarrow cos4x+cos4x.cos2x=0\)

\(\Leftrightarrow cos4x\left(cos2x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos4x=0\\cos2x=-1\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}4x=\frac{\pi}{2}+k\pi\\2x=\pi+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{8}+\frac{k\pi}{4}\\x=\frac{\pi}{2}+k\pi\end{matrix}\right.\)

b/

\(\Leftrightarrow cos\left(2x+\frac{\pi}{3}\right)+cos\left(\frac{\pi}{3}\right)+\sqrt{3}sin2x=1\)

\(\Leftrightarrow cos2x.cos\left(\frac{\pi}{3}\right)-sin2x.sin\left(\frac{\pi}{3}\right)+\frac{1}{2}+\sqrt{3}sin2x=1\)

\(\Leftrightarrow\frac{1}{2}cos2x+\frac{\sqrt{3}}{2}sin2x=\frac{1}{2}\)

\(\Leftrightarrow cos\left(2x-\frac{\pi}{3}\right)=\frac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{3}+k2\pi\\2x-\frac{\pi}{3}=-\frac{\pi}{3}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+k\pi\\x=k\pi\end{matrix}\right.\)

c/

\(\Leftrightarrow5+5cosx=2+\left(sin^2x-cos^2x\right)\left(sin^2x+cos^2x\right)\)

\(\Leftrightarrow3+5cosx=sin^2x-cos^2x\)

\(\Leftrightarrow3+5cosx=1-cos^2x-cos^2x\)

\(\Leftrightarrow2cos^2x+5cosx+2=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cosx=-2\left(l\right)\\cosx=-\frac{1}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{2\pi}{3}+k2\pi\\x=-\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)

a: Ta sẽ có hình vẽ sau:

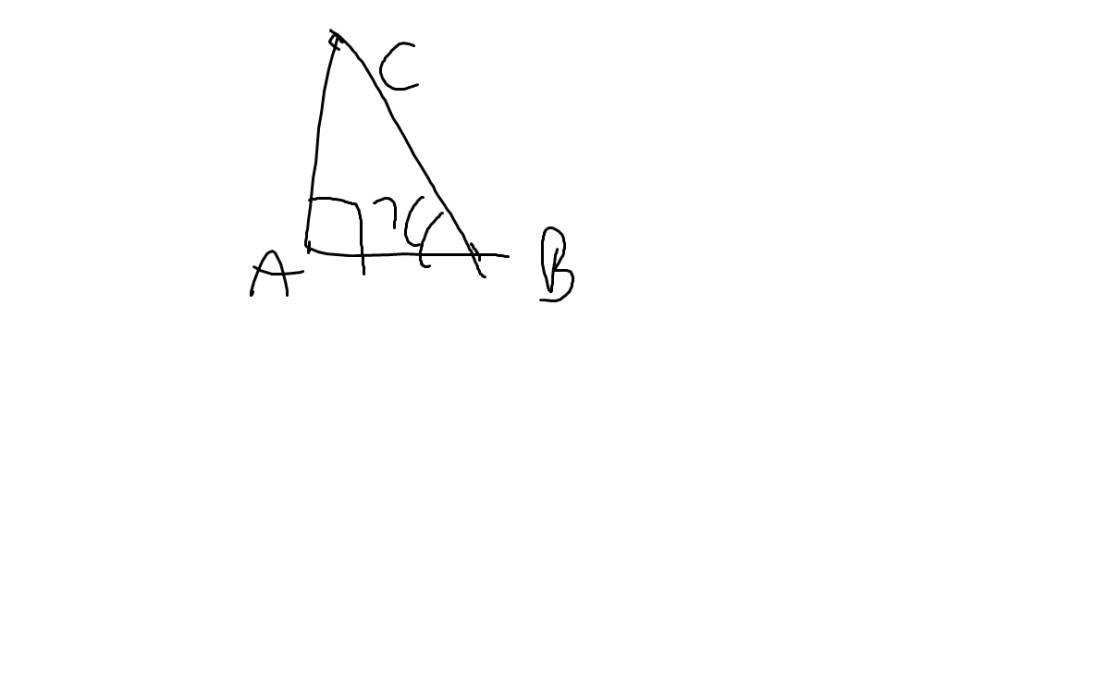
Đặt \(x=\widehat{B}\)

sin x=sin B=AC/BC

cosx=cosB=AB/BC

\(tanx=tanB=\dfrac{AC}{AB}=\dfrac{sinx}{cosx}\)

=>\(tan^2x=\dfrac{sin^2x}{cos^2x}\)

b: \(cot^2x=\dfrac{1}{tan^2x}=1:\dfrac{sin^2x}{cos^2x}=\dfrac{cos^2x}{sin^2x}\)

a: \(sin\left(x-\dfrac{\Omega}{4}\right)=-\dfrac{\sqrt{2}}{2}\)

=>\(sin\left(x-\dfrac{\Omega}{4}\right)=sin\left(-\dfrac{\Omega}{4}\right)\)

=>\(\left[{}\begin{matrix}x-\dfrac{\Omega}{4}=-\dfrac{\Omega}{4}+k2\Omega\\x-\dfrac{\Omega}{4}=\Omega+\dfrac{\Omega}{4}+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=k2\Omega\\x=\dfrac{3}{2}\Omega+k2\Omega\end{matrix}\right.\)

b: \(cos\left(x+\dfrac{\Omega}{4}\right)=cos\left(\dfrac{3}{4}\Omega\right)\)

=>\(\left[{}\begin{matrix}x+\dfrac{\Omega}{4}=\dfrac{3}{4}\Omega+k2\Omega\\x+\dfrac{\Omega}{4}=-\dfrac{3}{4}\Omega+k2\Omega\end{matrix}\right.\)

=>\(\left[{}\begin{matrix}x=\dfrac{1}{2}\Omega+k2\Omega\\x=-\Omega+k2\Omega\end{matrix}\right.\)

c: ĐKXĐ: \(\left\{{}\begin{matrix}2x< >\dfrac{\Omega}{2}+k\Omega\\x+\dfrac{\Omega}{3}< >\dfrac{\Omega}{2}+k\Omega\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x< >\dfrac{\Omega}{4}+\dfrac{k\Omega}{2}\\x< >\dfrac{1}{6}\Omega+k\Omega\end{matrix}\right.\)

\(tan2x=tan\left(x+\dfrac{\Omega}{3}\right)\)

=>\(2x=x+\dfrac{\Omega}{3}+k\Omega\)

=>\(x=\dfrac{\Omega}{3}+k\Omega\)

d: ĐKXĐ: \(2x< >k\Omega\)

=>\(x< >\dfrac{k\Omega}{2}\)

\(cot2x=-\dfrac{\sqrt{3}}{3}\)

=>\(cot2x=cot\left(-\dfrac{\Omega}{3}\right)\)

=>\(2x=-\dfrac{\Omega}{3}+k\Omega\)

=>\(x=-\dfrac{\Omega}{6}+\dfrac{k\Omega}{2}\)