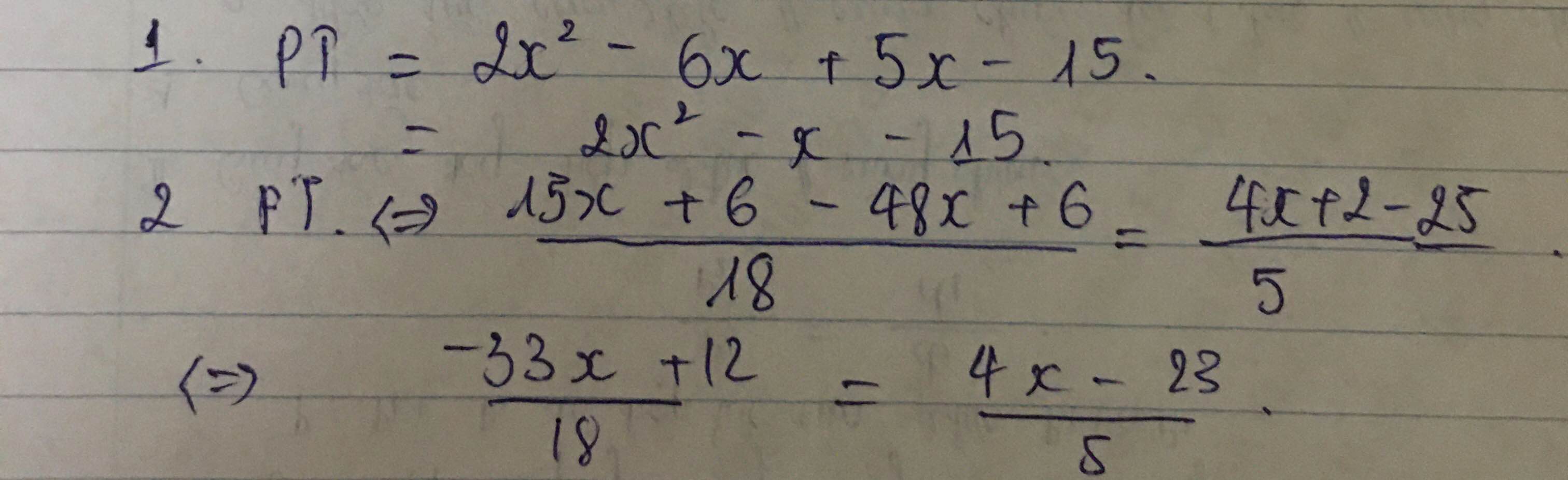1: \(\Leftrightarrow2x^2-10x-3x-2x^2=0\)

=>-13x=0

=>x=0

2: \(\Leftrightarrow5x-2x^2+2x^2-2x=13\)

=>3x=13

=>x=13/3

3: \(\Leftrightarrow4x^4-6x^3-4x^3+6x^3-2x^2=0\)

=>-2x^2=0

=>x=0

4: \(\Leftrightarrow5x^2-5x-5x^2+7x-10x+14=6\)

=>-8x=6-14=-8

=>x=1

`1)2x(x-5)-(3x+2x^2)=0`

`<=>2x^2-10x-3x-2x^2=0`

`<=>-13x=0`

`<=>x=0`

___________________________________________________

`2)x(5-2x)+2x(x-1)=13`

`<=>5x-2x^2+2x^2-2x=13`

`<=>3x=13<=>x=13/3`

___________________________________________________

`3)2x^3(2x-3)-x^2(4x^2-6x+2)=0`

`<=>4x^4-6x^3-4x^4+6x^3-2x^2=0`

`<=>x=0`

___________________________________________________

`4)5x(x-1)-(x+2)(5x-7)=0`

`<=>5x^2-5x-5x^2+7x-10x+14=0`

`<=>-8x=-14`

`<=>x=7/4`

___________________________________________________

`5)6x^2-(2x-3)(3x+2)=1`

`<=>6x^2-6x^2-4x+9x+6=1`

`<=>5x=-5<=>x=-1`

___________________________________________________

`6)2x(1-x)+5=9-2x^2`

`<=>2x-2x^2+5=9-2x^2`

`<=>2x=4<=>x=2`

a: ĐKXĐ: \(x\notin\left\{\dfrac{5}{2}\right\}\)

\(\log_32x-5=3\)

=>\(log_3\left(2x-5\right)=log_327\)

=>2x-5=27

=>2x=32

=>x=16(nhận)

b: ĐKXĐ: x<>0

\(\log_4x^2=2\)

=>\(log_4x^2=log_416\)

=>\(x^2=16\)

=>\(\left[{}\begin{matrix}x=4\left(nhận\right)\\x=-4\left(nhận\right)\end{matrix}\right.\)

c: ĐKXĐ: \(x\notin\left\{\dfrac{1}{3};-\dfrac{5}{2}\right\}\)

\(\log_7\left(3x-1\right)=\log_7\left(2x+5\right)\)

=>3x-1=2x+5

=>x=6(nhận)

d: ĐKXĐ: \(x\notin\left\{1;-1;\dfrac{-1+\sqrt{13}}{4};\dfrac{-1-\sqrt{13}}{4}\right\}\)

\(ln\left(4x^2+2x-3\right)=ln\left(3x^2-3\right)\)

=>\(4x^2+2x-3=3x^2-3\)

=>\(x^2+2x=0\)

=>x(x+2)=0

=>\(\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=-2\left(nhận\right)\end{matrix}\right.\)

e: ĐKXĐ: \(x\notin\left\{-\dfrac{3}{2};\dfrac{1}{3}\right\}\)

\(log\left(2x+3\right)=log\left(1-3x\right)\)

=>2x+3=1-3x

=>5x=-2

=>\(x=-\dfrac{2}{5}\left(nhận\right)\)

b: \(=2x^2-3x+10x-15=2x^2+7x-15\)

a) Ta có: \(\left(2x-3\right)^2=\left(2x-3\right)\left(x+1\right)\)

\(\Leftrightarrow\left(2x-3\right)^2-\left(2x-3\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left(2x-3\right)\left(2x-3-x-1\right)=0\)

\(\Leftrightarrow\left(2x-3\right)\left(x-4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=4\end{matrix}\right.\)

Vậy: \(S=\left\{\dfrac{3}{2};4\right\}\)

b) Ta có: \(x\left(2x-9\right)=3x\left(x-5\right)\)

\(\Leftrightarrow x\left(2x-9\right)-3x\left(x-5\right)=0\)

\(\Leftrightarrow x\left(2x-9\right)-x\left(3x-15\right)=0\)

\(\Leftrightarrow x\left(2x-9-3x+15\right)=0\)

\(\Leftrightarrow x\left(6-x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\6-x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)

Vậy: S={0;6}

c) Ta có: \(3x-15=2x\left(x-5\right)\)

\(\Leftrightarrow3\left(x-5\right)-2x\left(x-5\right)=0\)

\(\Leftrightarrow\left(x-5\right)\left(3-2x\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-5=0\\3-2x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{3}{2}\end{matrix}\right.\)

Vậy: \(S=\left\{5;\dfrac{3}{2}\right\}\)

d) Ta có: \(\dfrac{5-x}{2}=\dfrac{3x-4}{6}\)

\(\Leftrightarrow6\left(5-x\right)=2\left(3x-4\right)\)

\(\Leftrightarrow30-6x=6x-8\)

\(\Leftrightarrow30-6x-6x+8=0\)

\(\Leftrightarrow-12x+38=0\)

\(\Leftrightarrow-12x=-38\)

\(\Leftrightarrow x=\dfrac{19}{6}\)

Vậy: \(S=\left\{\dfrac{19}{6}\right\}\)

e) Ta có: \(\dfrac{3x+2}{2}-\dfrac{3x+1}{6}=2x+\dfrac{5}{3}\)

\(\Leftrightarrow\dfrac{3\left(3x+2\right)}{6}-\dfrac{3x+1}{6}=\dfrac{12x}{6}+\dfrac{10}{6}\)

\(\Leftrightarrow6x+4-3x-1=12x+10\)

\(\Leftrightarrow3x+3-12x-10=0\)

\(\Leftrightarrow-9x-7=0\)

\(\Leftrightarrow-9x=7\)

\(\Leftrightarrow x=-\dfrac{7}{9}\)

Vậy: \(S=\left\{-\dfrac{7}{9}\right\}\)

a, \(x^2\)  - 19 = 5.9

     \(x^2\) - 19 = 45

     \(x^2\)         = 45 + 19

     \(x^2\)         = 64

      \(x^2\)        = 8²

      \(x\)         = 8 

b, (2\(x\) + 1)³ = -0,001

    (2\(x\) + 1)³ = (-0,1)³

     2\(x\) + 1   = -0,1

     2\(x\)        = -0,1 - 1

     2\(x\)       = - 1,1

       \(x\)      = -1,1: 2

       \(x\)      = -  0,55

\(x^2-19=5\cdot9\\\Rightarrow x^2-19=45\\\Rightarrow x^2=45+19\\\Rightarrow x^2=64\\\Rightarrow x^2=(\pm8)^2\)

\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-8\end{matrix}\right.\)

\(---\)

\((2x+1)^3=-0,001\\\Rightarrow (2x+1)^3=(-0,1)^3\\\Rightarrow2x+1=-0,1\\\Rightarrow2x=-0,1-1\\\Rightarrow2x=-1,1\\\Rightarrow x=-1,1:2\\\Rightarrow x=\dfrac{-11}{20}\\---\)

\(\bigg(\dfrac56\bigg)^{2x-1}=\bigg(\dfrac56\bigg)^5\\\Rightarrow 2x-1=5\\\Rightarrow2x=5+1\\\Rightarrow2x=6\\\Rightarrow x=6:2\\\Rightarrow x=3\\---\)

\(\bigg(\dfrac13x-\dfrac23\bigg)^3=27\\\Rightarrow\bigg(\dfrac13x-\dfrac23\bigg)^3=3^3\\\Rightarrow\dfrac13x-\dfrac23=3\\\Rightarrow\dfrac13x=3+\dfrac23\\\Rightarrow\dfrac13x=\dfrac{11}{3}\\\Rightarrow x=\dfrac{11}{3}:\dfrac13\\\Rightarrow x=11\\---\)

\(\bigg(\dfrac{1}{32}\bigg)^x=\bigg(\dfrac12\bigg)^{15}\\\Rightarrow\bigg(\dfrac{1}{32}\bigg)^x=\bigg[\bigg(\dfrac{1}{2}\bigg)^5\bigg]^3\\\Rightarrow\bigg(\dfrac{1}{32}\bigg)^x=\bigg(\dfrac{1^5}{2^5}\bigg)^3\\\Rightarrow\bigg(\dfrac{1}{32}\bigg)^x=\bigg(\dfrac{1}{32}\bigg)^3\\\Rightarrow x=3\\Toru\)

Bài 1:

a) Ta có: \(\frac{4}{5}x-3=\frac{1}{5}x\left(4x-15\right)\)

\(\Leftrightarrow\frac{4x}{5}-3=\frac{4x^2}{5}-3x\)

\(\Leftrightarrow\frac{12x}{15}-\frac{45}{15}-\frac{12x^2}{15}+\frac{45x}{15}=0\)

Suy ra: \(12x-45-12x^2+45x=0\)

\(\Leftrightarrow-12x^2+57x-45=0\)

\(\Leftrightarrow-12x^2+12x+45x-45=0\)

\(\Leftrightarrow-12x\left(x-1\right)+45\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(-12x+45\right)=0\)

\(\Leftrightarrow-3\left(x-1\right)\left(4x-15\right)=0\)

mà \(-3\ne0\)

nên \(\left[{}\begin{matrix}x-1=0\\4x-15=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\4x=15\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\frac{15}{4}\end{matrix}\right.\)

Vậy: Tập nghiệm \(S=\left\{1;\frac{15}{4}\right\}\)

b) Ta có: \(\left(x-3\right)-\frac{\left(x-3\right)\left(2x-5\right)}{6}=\frac{\left(x-3\right)\left(3-x\right)}{4}\)

\(\Leftrightarrow\left(x-3\right)-\frac{\left(x-3\right)\left(2x-5\right)}{6}+\frac{\left(x-3\right)^2}{4}=0\)

\(\Leftrightarrow\frac{12\left(x-3\right)}{12}-\frac{2\left(x-3\right)\left(2x-5\right)}{12}+\frac{3\left(x-3\right)^2}{12}=0\)

Suy ra: \(12\left(x-3\right)-2\left(2x^2-11x+15\right)+3\left(x^2-6x+9\right)=0\)

\(\Leftrightarrow12x-36-4x^2+22x-30+3x^2-18x+27=0\)

\(\Leftrightarrow-x^2+16x-39=0\)

\(\Leftrightarrow-\left(x^2-16x+39\right)=0\)

\(\Leftrightarrow x^2-13x-3x+39=0\)

\(\Leftrightarrow x\left(x-13\right)-3\left(x-13\right)=0\)

\(\Leftrightarrow\left(x-13\right)\left(x-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-13=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=13\\x=3\end{matrix}\right.\)

Vậy: Tập nghiệm S={3;13}

c) Ta có: \(\frac{\left(3x+1\right)\left(3x-2\right)}{3}+5\left(3x+1\right)=\frac{2\left(2x+1\right)\left(3x+1\right)}{3}+2x\left(3x+1\right)\)

\(\Leftrightarrow\frac{9x^2-3x-2}{3}+5\left(3x+1\right)-\frac{12x^2+10x+2}{3}-2x\left(3x+1\right)=0\)

\(\Leftrightarrow\frac{9x^2-3x-2-12x^2-10x-2}{3}-6x^2+13x+5=0\)

\(\Leftrightarrow\frac{-3x^2-13x-4}{3}+\frac{3\left(-6x^2+13x+5\right)}{3}=0\)

Suy ra: \(-3x^2-13x-4-18x^2+39x+15=0\)

\(\Leftrightarrow-21x^2+26x+11=0\)

\(\Leftrightarrow-21x^2-7x+33x+11=0\)

\(\Leftrightarrow-7x\left(3x+1\right)+11\left(3x+1\right)=0\)

\(\Leftrightarrow\left(3x+1\right)\left(-7x+11\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}3x+1=0\\-7x+11=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=-1\\-7x=-11\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{-1}{3}\\x=\frac{11}{7}\end{matrix}\right.\)

Vậy: Tập nghiệm \(S=\left\{-\frac{1}{3};\frac{11}{7}\right\}\)

\(1,\) thiếu đề

\(2,\dfrac{5x+2}{6}-\dfrac{8x-1}{3}=\dfrac{4x+2}{5}-5\)

\(\Leftrightarrow\dfrac{5\left(5x+2\right)}{30}-\dfrac{10\left(8x-1\right)}{30}=\dfrac{6\left(4x+2\right)}{30}-\dfrac{150}{30}\)

\(\Leftrightarrow5\left(5x+2\right)-10\left(8x-1\right)=6\left(4x+2\right)-150\)

\(\Leftrightarrow25x+10-80x+10=24x+12-150\)

\(\Leftrightarrow-55x+20=24x-138\)

\(\Leftrightarrow24x-138+55x-20=0\)

\(\Leftrightarrow79x-158=0\)

\(\Leftrightarrow x=2\)

\(3,ĐKXĐ:\left\{{}\begin{matrix}x\ne1\\x\ne-1\\x\ne3\end{matrix}\right.\\ \dfrac{x}{2x-6}+\dfrac{x}{2x-2}=\dfrac{-2x}{\left(x+1\right)\left(3-x\right)}\)

\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}+\dfrac{2x}{\left(x+1\right)\left(3-x\right)}=0\)

\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}-\dfrac{2x}{\left(x+1\right)\left(x-3\right)}=0\)

\(\Leftrightarrow x\left(\dfrac{1}{2\left(x-3\right)}+\dfrac{1}{2\left(x-1\right)}-\dfrac{2}{\left(x+1\right)\left(x-3\right)}\right)=0\)

\(\Leftrightarrow x\left(\dfrac{\left(x-1\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4\left(x-1\right)}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)

\(\Leftrightarrow x\left(\dfrac{x^2-1}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{x^2-2x-3}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4x-4}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)

\(\Leftrightarrow x.\dfrac{x^2-1+x^2-2x-3-4x+4}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)

\(\Leftrightarrow x.\dfrac{2x^2-6x}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)

\(\Leftrightarrow x.\dfrac{2x\left(x-3\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)

\(\Leftrightarrow x.\dfrac{x}{\left(x-1\right)\left(x+1\right)}=0\)

\(\Leftrightarrow\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}=0\)

\(\Leftrightarrow x=0\)