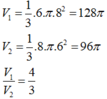Cho ΔABC vuông tại A, AB < AC; vẽ AH ⊥ BC. Trên tia đối HA lấy D sao cho HA = HD. Trên tia BC lấy K sao cho HK = HB
CMR: a) ΔAHK = ΔDHB
b) AK // BD
c) AB = BD
d) Ba điểm D, K, I thẳng hàng ( KI ⊥ AC tại I )

Những câu hỏi liên quan
Cho ΔABC vuông tại B biết: BC=2a; góc A=45°: a) Tính độ dài cạnh AB; AC b) Kẻ BH vuông góc AC. Tính BH=? c) Tính diện tích ΔABC d) Tính chu vi ΔABC e) Tính bán kính đường tròn ngoại tiếp ΔABC
a: ΔBAC vuông tại B có góc A=45 độ
nên ΔBAC vuông cân tại B
=>BA=BC=2a
AC=căn AB^2+BC^2=2a*căn 2
b: BH=BA*BC/AC=4a^2/2*a*căn 2=a*căn 2
c: S ABC=1/2*2a*2a=2a^2
d: C=2a+2a+2a*căn 2=4a+2a*căn 2
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A (AC > AB), đường cao AH. Trên tia HC lấy điểm D sao cho HD = AH. Qua D kẻ đường thẳng vuông góc với BC, cắt cạnh AC tại E.
C/m: a) ΔABC ∼ ΔHAC.
b) EC . AC = DC . BC.
c) ΔBEC ∼ ΔADC.
cho ΔABC vuông tại A. Trên tia đối tia AB, lấy điểm sao cho AD=AB
a. cm= ΔABC=ΔADC
b. Trên tia đối tia AC lấy điểm E sao cho AE=AC. Chứng minh BC//DE
a: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AB=AD
AC chung
Do đó: ΔABC=ΔADC
b: Xét tứ giác BCDE có
A là trung điểm của BD
A là trung điểm của CE
Do đó: BCDE là hình bình hành
Suy ra: BC//DE
Đúng 1
Bình luận (0)
: Cho ΔABC vuông tại A có AB = 5cm, AC = 12cm.
a/ Tính BC.
b/ Trên tia đối của tia AB lấy điểm D sao cho AD = AB. Chứng minh ΔABC = ΔADC.
c/ Chứng minh : BCD cân tại C.
d/ Vẽ đường thẳng qua A song song với BC cắt CD tại E, BE cắt AC tại G. Chứng minh : G là
trọng tâm của BDC. ( Dành cho các lớp 7 A, B, C)
CÂU D THOI CX ĐC:))
a: \(BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔADC vuông tại A có
AC chung
AB=AD
Do đó: ΔABC=ΔADC
c: Ta có: ΔABC=ΔADC
nên BC=DC
hay ΔCBD cân tại C
Đúng 0
Bình luận (0)
Cho ΔABC có AB=AC. AD là tia phân giác của góc A. cho AH vuông góc với AB tại H, AK vuông góc với AC tại K.
Chứng minh ΔABD=ΔACD
Chứng minh ΔHBD=ΔKCD
a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
b: Đề sai rồi bạn
Đúng 0
Bình luận (0)
Cho tam giác ΔABC vuông tại A có AB=6cm,AC=10cm . Đường cao AH a)Chứng minh ΔABC / ΔABH b)Chứng minh AB²=BH.BC c)Tính BC,AH,BH
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)
Đúng 1
Bình luận (0)
a.Xét tam giác ABC và tam giác HBA, có:
^B: chung
^BAC = ^BHA = 90 độ
Vậy tam giác ABC đồng dạng tam giác HBA (g.g)
b.\(\rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)
\(\Leftrightarrow AB^2=BH.BC\left(đfcm\right)\) (1)
c.Áp dụng định lý pitago \(\Rightarrow BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)
(1) \(\Leftrightarrow6^2=2\sqrt{34}BH\)
\(\Leftrightarrow BH=\dfrac{9\sqrt{34}}{17}\left(cm\right)\)
Áp dụng định lý pitago trong tam giác ABH \(\Rightarrow AH=\sqrt{6^2-\left(\dfrac{9\sqrt{34}}{17}\right)^2}=\dfrac{15\sqrt{34}}{17}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A. Tính AB biết HB = 2cm; HC=8cm, AC=6cm
Anh bổ sung là : AH vuông góc với BC nhé
\(BC=HB+HC=2+8=10\left(cm\right)\)
\(\text{Áp dụng định lý Pytago trong tam giác ABC vuông tại A:}\)
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{10^2-6^2}=8\left(cm\right)\)
Đúng 1
Bình luận (0)
Bổ sung đề \(AH\) là đường cao.
Áp dụng hệ thức lượng vào tam giác vuông \(ABC\) và đường cao \(AH\) ta có :
\(AB^2=BC.BH\)
\(\Rightarrow AB=\sqrt{BC.BH}=\sqrt{\left(8+2\right).2}=\sqrt{20}=2\sqrt{5}\)\((cm)\)
Đúng 1
Bình luận (0)
Đề bài sai rồi em
Nếu H là chân đường cao trên BC thì tam giác HAC vuông tại H
Khi đó trong tam giác vuông HAC có AC là cạnh huyền và CH là cạnh góc vuông
Nhưng CH=8>AC=6 là hoàn toàn vô lý
Đúng 1
Bình luận (0)
Cho ΔABC vuông tại A, AB 6cm, AC 8cm. Gọi V1 là thể tích khối nón tạo thành khi quay ΔABC quanh cạnh AB và V2 là thể tích khối nón tạo thành khi quay ΔABC quanh cạnh AC. Tỉ số V1/ V2 bằng A. 4/3 B. 3/4 C. 16/9 D. 64/27
Đọc tiếp
Cho ΔABC vuông tại A, AB = 6cm, AC = 8cm. Gọi V1 là thể tích khối nón tạo thành khi quay ΔABC quanh cạnh AB và V2 là thể tích khối nón tạo thành khi quay ΔABC quanh cạnh AC. Tỉ số V1/ V2 bằng
A. 4/3
B. 3/4
C. 16/9
D. 64/27
Cho ΔABC vuông tại A, có AH vuông góc BC. Tính AB biết HB = 2cm; HC=8cm, AC=6cm
\(BC=BH+HC=2+8=10\left(cm\right)\)
△ABC vuông tại A có \(BC^2=AB^2+AC^2\\ \Rightarrow AB^2=BC^2-AC^2=10^2-6^2=64\\ \Rightarrow AB=8\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho ΔABC vuông tại A, đường cao AH. Gọi E,F lầ lượt là hình chiếu của H trên AB và AC a) Chứng minh ΔAFE ∼ ΔABC b) Chứng minh AH^3 BC.BE.CF
Đọc tiếp
Cho ΔABC vuông tại A, đường cao AH. Gọi E,F lầ lượt là hình chiếu của H trên AB và AC a) Chứng minh ΔAFE ∼ ΔABC b) Chứng minh AH^3= BC.BE.CF
Lời giải:
a. Áp dụng HTL trong tam giác vuông ta có:
$AE.AB=AH^2$
$AF.AC=AH^2$
$\Rightarrow AE.AB=AF.AC\Rightarrow \frac{AE}{AF}=\frac{AC}{AB}$
Xét tam giác $AFE$ và $ABC$ có:
$\widehat{EAF}=\widehat{CAB}=90^0$
$\frac{AE}{AF}=\frac{AC}{AB}$ (cmt)
$\Rightarrow \triangle AFE\sim \triangle ABC$ (c.g.c)
b.
Áp dụng HTL trong tam giác vuông:
$BE.BA=BH^2$
$CF.CA=CH^2$
$\Rightarrow BE.CF.AB.AC=(BH.CH)^2=(AH^2)^2$
$\Leftrightarrow BE.CF.2S_{ABC}=AH^4$
$\Leftrightarrow BE.CF.AH.BC=AH^4$
$\Leftrightarrow BE.CF.BC=AH^3$ (đpcm)
Đúng 1
Bình luận (0)