Tìm a,b,c thuộc Z thỏa mãn
\(\left\{{}\begin{matrix}2a+3b=5\\3a-4c=6\end{matrix}\right.\)
1.Cho\(\left\{{}\begin{matrix}a,b,c>0\\a+2b+3c=20\end{matrix}\right.\)Tìm GTNN
P=\(2a+3b+4c+\dfrac{3}{a}+\dfrac{9}{2b}+\dfrac{4}{c}\)
\(P=\dfrac{5a+10b+15c}{4}+\left(\dfrac{3}{a}+\dfrac{3a}{4}\right)+\left(\dfrac{9}{2b}+\dfrac{b}{2}\right)+\left(\dfrac{4}{c}+\dfrac{c}{4}\right)\)
\(\ge\dfrac{5\left(a+2b+3c\right)}{4}+2\sqrt{\dfrac{3}{a}.\dfrac{3a}{4}}+2\sqrt{\dfrac{9}{2b}.\dfrac{b}{2}}+2\sqrt{\dfrac{4}{c}.\dfrac{c}{4}}\)
\(\Leftrightarrow P\ge\dfrac{5.20}{4}+3+3+2=33\)
Dấu "=" xảy ra khi a=2;b=3;c=4
Vậy \(P_{min}=33\)
Giải hệ phương trình :
\(\left\{{}\begin{matrix}a+2b+3c=10\\2a+3b+c=13\\3a+b+2c=13\end{matrix}\right.\)
Bấm máy tính Casio fx-570 VN giải hệ phương trình 3 ẩn
Mode\(\rightarrow\) 5\(\rightarrow\) 2 :
| Hệ số | a | b | c | d |
| PT 1 | 1 | 2 | 3 | 10 |
| PT 2 | 2 | 3 | 1 | 13 |
| PT 3 | 3 | 1 | 2 | 13 |
Ấn dấu = ta được a=3, b=2, c=1 (trên màn hình máy tính là x,y,z)
2 Pt đầu khử a ,2 pt sau khử a ,ta được HPT 2 ẩn b,c
Giải hpt : \(\left\{{}\begin{matrix}a^3-3a-2=2-b\\b^3-3b-2=4-2c\\c^3-3c-2=6-3a\end{matrix}\right.\)
1.\(\left\{{}\begin{matrix}a,b>0\\2a+3b=4\end{matrix}\right.\)Tìm GTNN của
M=\(\dfrac{2002}{a}+\dfrac{2017}{b}+2096a-5501b\)
Bài này mình làm lâu rồi á bann sửa dấu `2a+3b<=4` thành `2a+3b=4` nhé!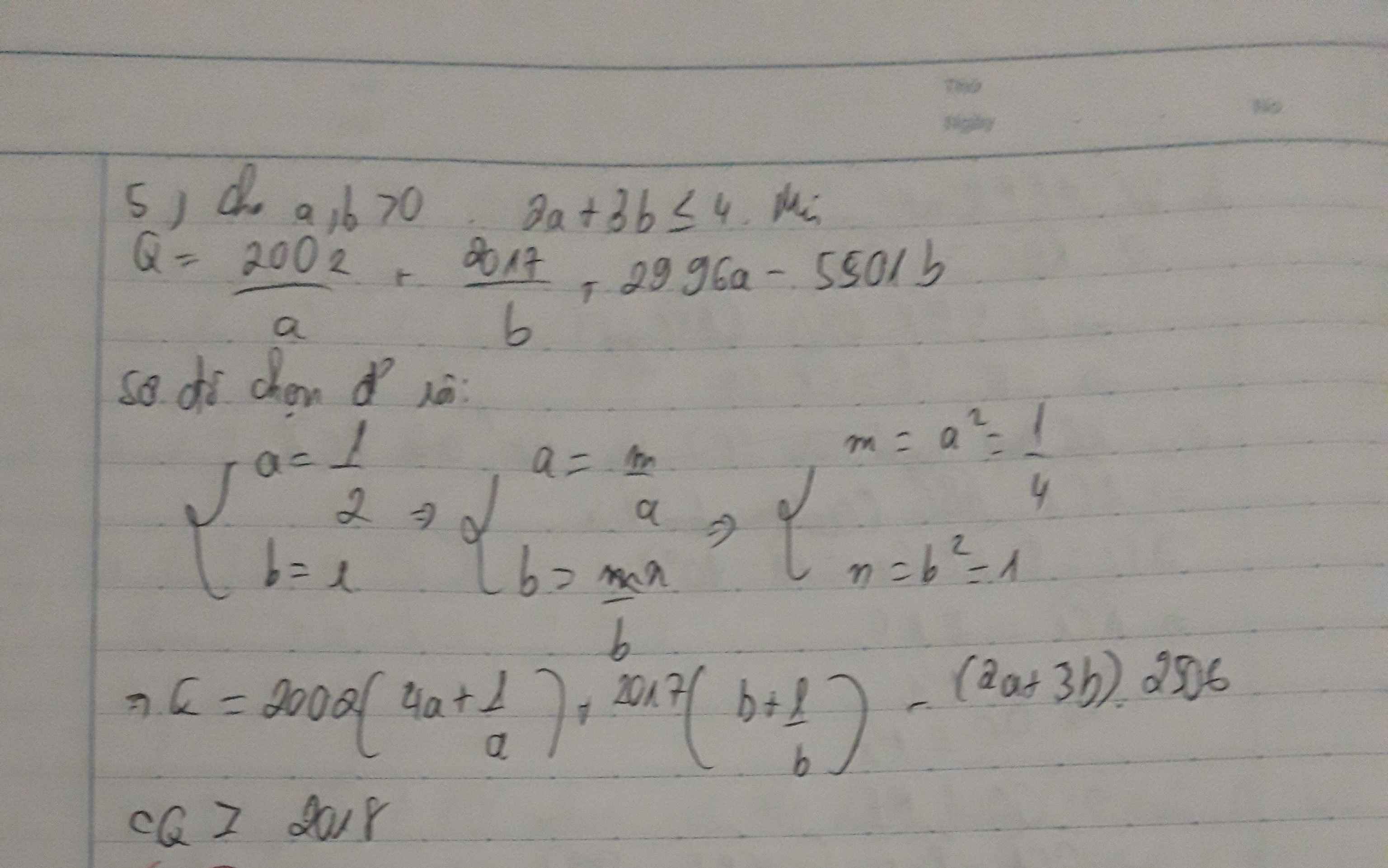
Tìm x,y,z thỏa mãn hệ sau:
\(\left\{{}\begin{matrix}x^3-3x-2=2-y\\y^3-3y-2=4-2z\\z^3-3z-2=6-3x\end{matrix}\right.\)
a) Cho x,y,z thỏa mãn x+y+z+xy+yz+zx=6. Tìm Min \(P=x^2+y^2+z^2\)
giải hệ pt : 1) \(\left\{{}\begin{matrix}\dfrac{1}{\sqrt{x}}+\sqrt{2-\dfrac{1}{y}}=2\\\dfrac{1}{\sqrt{y}}+\sqrt{2-\dfrac{1}{x}}=2\end{matrix}\right.\)
2) \(\left\{{}\begin{matrix}x^2+xy+y^2=7\\x^4+x^2y^2+y^4=21\end{matrix}\right.\)
1. Với mọi số thực x;y;z ta có:
\(x^2+y^2+z^2+\dfrac{1}{2}\left(x^2+1\right)+\dfrac{1}{2}\left(y^2+1\right)+\dfrac{1}{2}\left(z^2+1\right)\ge xy+yz+zx+x+y+z\)
\(\Leftrightarrow\dfrac{3}{2}P+\dfrac{3}{2}\ge6\)
\(\Rightarrow P\ge3\)
\(P_{min}=3\) khi \(x=y=z=1\)
1.1
ĐKXĐ: ...
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{\sqrt{x}}=a>0\\\dfrac{1}{\sqrt{y}}=b>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a+\sqrt{2-b^2}=2\\b+\sqrt{2-a^2}=2\end{matrix}\right.\)
\(\Rightarrow a-b+\sqrt{2-b^2}-\sqrt{2-a^2}=0\)
\(\Leftrightarrow a-b+\dfrac{\left(a-b\right)\left(a+b\right)}{\sqrt{2-b^2}+\sqrt{2-a^2}}=0\)
\(\Leftrightarrow a=b\Leftrightarrow x=y\)
Thay vào pt đầu:
\(a+\sqrt{2-a^2}=2\Rightarrow\sqrt{2-a^2}=2-a\) (\(a\le2\))
\(\Leftrightarrow2-a^2=4-4a+a^2\Leftrightarrow2a^2-4a+2=0\)
\(\Rightarrow a=1\Rightarrow x=y=1\)
2.
\(\left\{{}\begin{matrix}x^2+xy+y^2=7\\\left(x^2+y^2\right)^2-x^2y^2=21\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+xy+y^2=7\\\left(x^2+xy+y^2\right)\left(x^2-xy+y^2\right)=21\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+xy+y^2=7\\x^2-xy+y^2=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x^2+3xy+3y^2=21\\7x^2-7xy+7y^2=21\end{matrix}\right.\)
\(\Rightarrow4x^2-10xy+4y^2=0\)
\(\Leftrightarrow2\left(2x-y\right)\left(x-2y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y=2x\\y=\dfrac{1}{2}x\end{matrix}\right.\)
Thế vào pt đầu
...
Cho a, b , c ko âm và thỏa mãn \(\hept{\begin{cases}2a+b+2c=6\\3a+4b-3c=4\end{cases}}\) . Tìm GTLN và GTNT của P = 2a + 3b - 4c
Bạn nào zúp vs ạ !!!
\(\hept{\begin{cases}2a+b+2c=6\\3a+4b-3c=4\end{cases}}\)\(\Rightarrow a+3b-5c=-2\)
\(\Rightarrow3b=-2+5c-a\)\(\Rightarrow3b+2a-4c=-2+5c-a+2a-4c\)
\(\Rightarrow P=-2+a+c\)
Lại có : \(2a+b+2c=6\Rightarrow2\left(a+c\right)\le6\)
\(\Rightarrow a+c\le3\)
\(\Rightarrow P\le-2+3=1\Rightarrow P\le1\)
Dấu " = " sảy ra \(\Leftrightarrow\hept{\begin{cases}b=0\\3a-3c=4\\2a+2c=6\end{cases}}\)\(\Rightarrow\hept{\begin{cases}b=0\\3a-3c=4\\3a+3c=9\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}a=\frac{13}{6}\\b=0\\c=\frac{5}{6}\end{cases}}\)
Chị chỉ tìm được Max thui
\(\hept{\begin{cases}2a+b+2c=6\\3a+4b-3c=4\end{cases}}\)
<=> \(\hept{\begin{cases}b+2c=6-2a\\4b-3c=4-3a\end{cases}}\)
<=> \(\hept{\begin{cases}c=\frac{20}{11}-\frac{5a}{11}\\b=\frac{26}{11}-\frac{12}{11}a\end{cases}}\)
P = \(2a+3\left(\frac{26}{11}-\frac{12}{11}a\right)-4\left(\frac{20}{11}-\frac{5a}{11}\right)\)
\(=-\frac{2}{11}+\frac{6}{11}a\ge-\frac{2}{11}\)
Dấu "=" xảy ra <=> a = 0 => c =20/11 và b = 26/11
Vậy min P = -2/11 tại a = 0; b = 26/11 và c= 20/11
Cách tìm max khác:
Ta có: \(\hept{\begin{cases}2a+b+2c=6\\3a+4b-3c=4\end{cases}}\)
<=> \(\hept{\begin{cases}2a+2c=6-b\\3a-3c=4-4b\end{cases}}\) <=> \(\hept{\begin{cases}a+c=3-\frac{b}{2}\\a-c=\frac{4}{3}-\frac{4b}{3}\end{cases}}\)
<=> \(\hept{\begin{cases}a=\frac{13}{6}-\frac{11b}{12}\\c=\frac{5}{6}+\frac{5}{12}b\end{cases}}\)
khi đó P = \(2\left(\frac{13}{6}-\frac{11b}{12}\right)+3b-4\left(\frac{5}{6}+\frac{5}{12}b\right)=1-\frac{1}{2}b\le1\)
Dấu bằng xảy ra khi và chỉ khi b = 0 khi đó a = 13/6 và c = 5/6( thỏa mãn)
Vậy maxP = 1 tại a = 13/6 ; b = 0 ; c = 5/6.
Giải pt: \(\left\{{}\begin{matrix}3a^2+2ab+3b^2=12\\a^2+b^2=c^2\end{matrix}\right.\)
Cho HPT: \(\left\{{}\begin{matrix}3x+my=m\\\left(m-1\right)x+2y=m-1\end{matrix}\right.\)
a, Giải HPT khi m = -3
b, Tìm m để HPT có nghiệm duy nhất (x;y) thỏa mãn điều kiện x + y2 = 1
a. Bạn tự giải
b. \(\left\{{}\begin{matrix}6x+2my=2m\\\left(m^2-m\right)x+2my=m^2-m\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}6x+2my=2m\\\left(m^2-m-6\right)x=m^2-3m\end{matrix}\right.\)
Hệ có nghiệm duy nhất khi \(m^2-m-6\ne0\Rightarrow m\ne\left\{-2;3\right\}\)
Khi đó: \(\left\{{}\begin{matrix}x=\dfrac{m}{m+2}\\y=\dfrac{m-1}{m+2}\end{matrix}\right.\)
\(x+y^2=1\Leftrightarrow\dfrac{m}{m+2}+\left(\dfrac{m-1}{m+2}\right)^2=1\)
\(\Leftrightarrow m^2-4m-3=0\)
\(\Leftrightarrow...\)