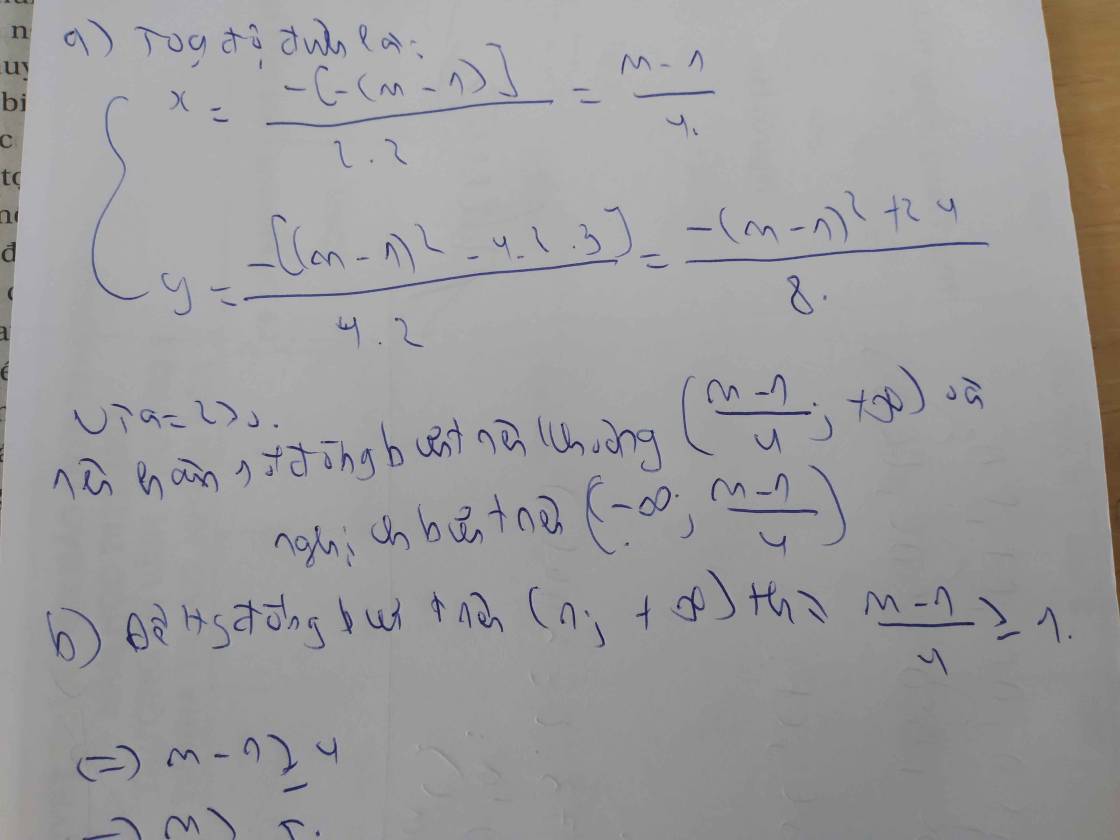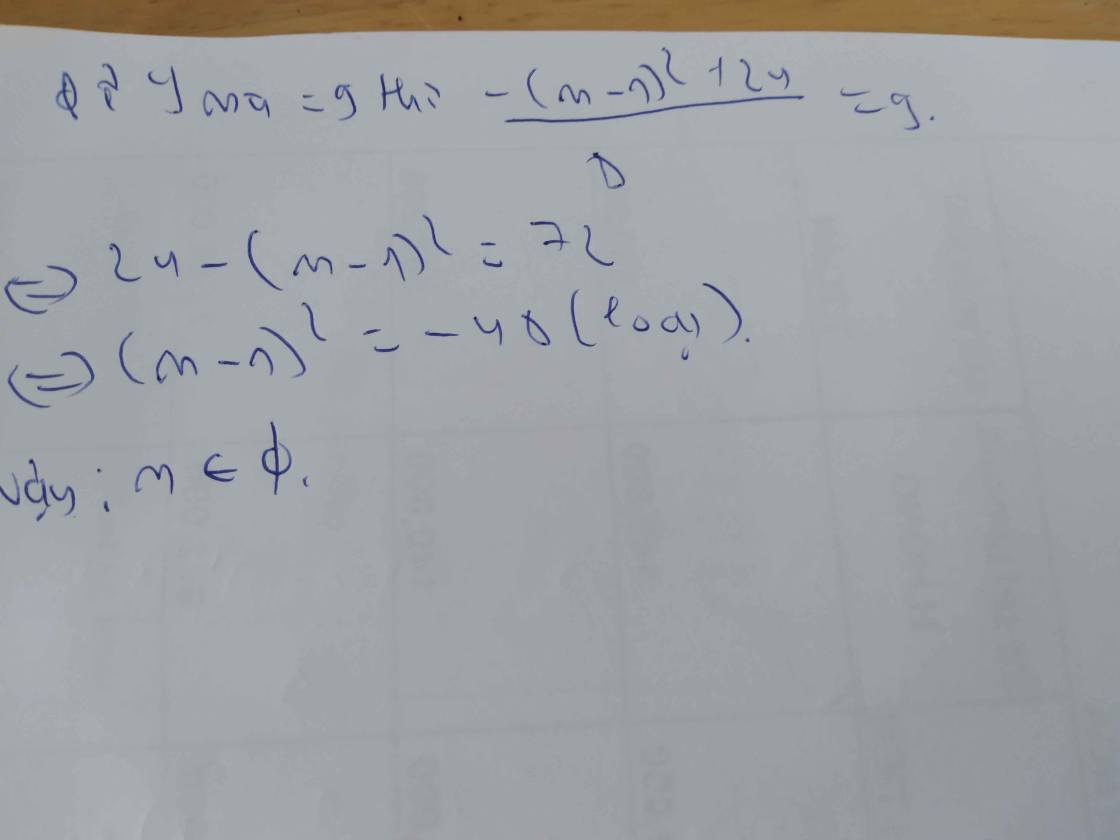a: Để hàm số trên là hàm số bậc nhất thì \(\left\{{}\begin{matrix}m\ge0\\m\ne4\end{matrix}\right.\)

b: Để hàm số đồng biến thì \(\sqrt{m}-2>0\)

hay m>4

\(\Leftrightarrow\) Với mọi \(x>1\) thì:

\(y'=\dfrac{x+m}{\sqrt{x^2+2mx+m^2+1}}\ge0\)

\(\Leftrightarrow x\ge-m\) (\(\forall x>1\))

\(\Leftrightarrow-m\le1\)

\(\Leftrightarrow m\ge-1\)

\(\dfrac{\sqrt{3}}{2}< 1;\dfrac{\sqrt[3]{26}}{3}< 1;\pi>1;\dfrac{\sqrt{15}}{4}< 1\)

Hàm số đồng biến là: \(log_{\pi}x\)

Hàm số nghịch biến là: \(\left(\dfrac{\sqrt{3}}{2}\right)^x;\left(\dfrac{\sqrt[3]{26}}{3}\right)^x;log_{\dfrac{\sqrt{15}}{4}}x\)

\(y'=-x^2+2\left(a-1\right)x+a+3\)

Hàm đồng biến trên khoảng đã cho khi với mọi \(x\in\left(0;3\right)\) ta có:

\(-x^2+2\left(a-1\right)x+a+3\ge0\)

\(\Leftrightarrow\left(2x+1\right)a\ge x^2+2x-3\)

\(\Rightarrow a\ge\dfrac{x^2+2x-3}{2x+1}\)

Xét hàm \(f\left(x\right)=\dfrac{x^2+2x-3}{2x+1}\) với \(x\in\left(0;3\right)\)

\(f'\left(x\right)=\dfrac{2\left(x^2+x+4\right)}{\left(2x+1\right)^2}>0\Rightarrow f\left(x\right)\) đồng biến

\(\Rightarrow f\left(x\right)< f\left(3\right)=\dfrac{12}{7}\Rightarrow a\ge\dfrac{12}{7}\)

a: TXĐ: D=R\{-1}

\(y'=\dfrac{\left(x+m\right)'\left(x+1\right)-\left(x+1\right)'\left(x+m\right)}{\left(x+1\right)^2}\)

\(=\dfrac{x+1-x-m}{\left(x+1\right)^2}=\dfrac{1-m}{\left(x+1\right)^2}\)

Để hàm số nghịch biến trên từng khoảng xác định thì \(y'< 0\forall x\)

=>\(\dfrac{1-m}{\left(x+1\right)^2}< 0\)

=>1-m<0

=>m>1

b: TXĐ: D=R\{m}

\(y=\dfrac{2x-3m}{x-m}\)

=>\(y'=\dfrac{\left(2x-3m\right)'\left(x-m\right)-\left(2x-3m\right)\left(x-m\right)'}{\left(x-m\right)^2}\)

\(=\dfrac{2\left(x-m\right)-\left(2x-3m\right)}{\left(x-m\right)^2}=\dfrac{2x-2m-2x+3m}{\left(x-m\right)^2}\)

\(=\dfrac{m}{\left(x-m\right)^2}\)

Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\)

=>\(\dfrac{m}{\left(x-m\right)^2}>0\)

=>m>0

Ta có \(y'=\frac{x^2-2mx+m^2}{\left(x-2m\right)^2},x\ne2m\)

Để y có hai khoảng đồng biến trên toàn miền xác định thì

\(y'\ge0,\forall x\ne2m\)

\(\Leftrightarrow x^2-4mx+m^2\ge0,\forall x\ne2m\)

\(\Leftrightarrow\Delta'\le0\Leftrightarrow4m^2-m^2\le0\)

\(\Leftrightarrow3m^2\le0\Leftrightarrow m=0\)

Câu tiếp theo:

y đồng biến trên\(\left(1,\infty\right)\Leftrightarrow y'\ge0,\forall x\in\left(1,+\infty\right)\)

     \(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=x^2-4mx+m^2\ge0,\forall x>1\\2m\notin\left(1,\infty\right)\end{cases}}\)

Để cj suy nghĩ mai lm tiếp=.=

rõ ràng m=0 thì đk trên thõa mãn.

Với \(m=0:\Delta'=3m^2>0\) nên ta có:

\(f\left(x\right)\ge0,\forall x>1\Leftrightarrow x_1< x_2\le1\)

\(\Leftrightarrow\hept{\begin{cases}\Delta'>0\\f\left(1\right)\ge\\\frac{S}{2}-1< 0\end{cases}0}\)

\(f\left(1\right)\ge0\Leftrightarrow m^2-4m+1\ge0\Leftrightarrow m\le2-\sqrt{3}\)hay\(m\ge2+\sqrt{3}\)

\(\frac{S}{2}-1< 0\Leftrightarrow2m-1< 0\Leftrightarrow m< \frac{1}{2}\)

\(2m\notin\left(1,\infty\right)\Leftrightarrow2m\le1\Leftrightarrow m\le\frac{1}{2}\)

Vậy \(m\le2-\sqrt{3}\)là giá trị m cần tìm

B. Hàm số nghịch biến trên khoảng \(\left(-\infty;-1\right)\)

Ta có \(y'=-2x^2+2\left(m+1\right)x+2m\)

Hàm số đồng biến trên khoảng (0;2) \(\Leftrightarrow y'\ge0,x\in\left(0;2\right)\) (*)

Vì y'(x) liên tục tại x=0 và x=2 nên (*) \(\Leftrightarrow y'\ge0,x\in\left[0;2\right]\)

\(\Leftrightarrow-2x^2+2\left(m+1\right)x+2m\ge0,x\in\left[0;2\right]\)

\(\Leftrightarrow m\left(x+1\right)\ge x^2-x,x\in\left[0;2\right]\Leftrightarrow m\ge g\left(x\right),x\in\left[0;2\right]\); (trong đó \(g\left(x\right)=\frac{x^2-x}{x+1}\))

\(\Leftrightarrow m\ge Max_{\left[0;2\right]}g\left(x\right)\)

Xét hàm số \(g\left(x\right)=\frac{x^2-x}{x+1}\) trên đoạn \(\left[0;2\right]\)

\(\Rightarrow g'\left(x\right)=\frac{x^2+2x-1}{\left(x+1\right)^2}\Rightarrow g'\left(x\right)=0\Leftrightarrow x=-1+\sqrt{2},x\in\left[0;2\right]\)

\(g\left(0\right);g\left(2\right)=\frac{2}{3};g\left(-1+\sqrt{2}\right)\Rightarrow Max_{\left(0;+\infty\right)}g\left(x\right)=\frac{2}{3}\) tại x=2

Vậy \(m\ge\frac{2}{3}\) thì hàm số đồng biến trên khoảng (0;2)

Ta có : \(y'=-2x^2+2\left(m+1\right)x+2m,\Delta'=m^2+6m+1\)

Suy ra hàm đồng biến trên khoảng (0; 2) \(\Leftrightarrow y'\ge0,x\in\left(0;2\right)\)(*)

Trường hợp 1 : Nếu \(\Delta'\le0\Leftrightarrow m^2+6m+1\le0\Leftrightarrow-3-2\sqrt{2}\le m\le-3+2\sqrt{2}\)

theo định lí về dấu tam thức bậc 2 ta có \(y'\le0,x\in R\) => (*) không thỏa mãn

Trường hợp 2 : Nếu \(\Delta'>0\Leftrightarrow m^2+6m+1>0\Leftrightarrow m\le-3-2\sqrt{2}\) hoặc \(m\ge-3+2\sqrt{2}\) thì (*) đúng

<=> phương trình \(y'=0\) có 2 nghiệm phân biệt \(x_1;x_2\) (\(x_1\)>\(x_2\)) và thỏa mãn \(x_1\le0<2\le x_2\)

\(\Leftrightarrow\begin{cases}\Delta>0\\x_1\le0<2\le x_2\end{cases}\) \(\Leftrightarrow\begin{cases}\left(x_1-2\right)\left(x_2-2\right)\le0\\\Delta>0\\\left(x_1-0\right)\left(x_2-0\right)\le0\end{cases}\)

\(\Leftrightarrow\begin{cases}x_1x_2-2\left(x_1+x_2\right)+4\le0\\\Delta>0\\x_1x_2\le0\end{cases}\)

\(\Leftrightarrow m\ge\frac{2}{3}\)

Kết hợp trường hợp 1 và trường hợp 2 ta có \(m\ge\frac{2}{3}\) thì hàm đồng biến trên khoảng (0;2)