Cho a // b. Cho \(\widehat{A_1}=130^0.\) Tính \(\widehat{B^{ }_1}\) ; \(\widehat{B_2}\) ; \(\widehat{B_3};\widehat{B_4}\)

Những câu hỏi liên quan
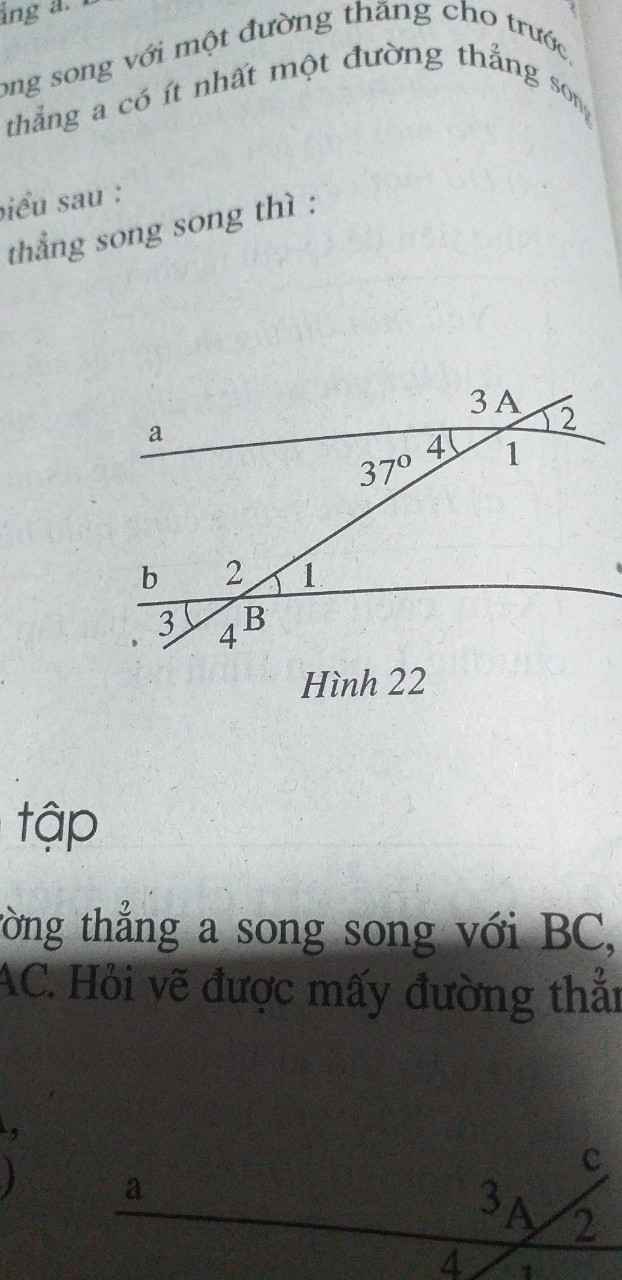
Hình 22 cho biết a // b và \(\widehat{A}_4\) = \(37^o\) .
a) Tính \(\widehat{B_1}\) .
b) So sánh \(\widehat{A_1}\) và \(\widehat{B_4}\) .
c) Tính \(\widehat{B_2}\)
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác
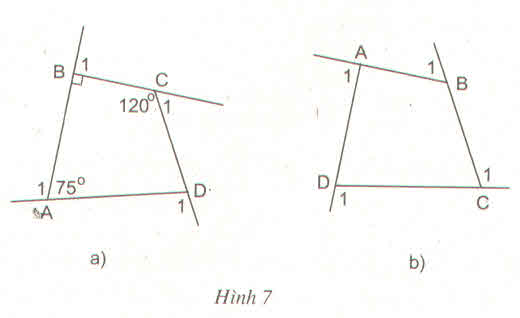
a) Tính các góc ngoài của tứ giác ở hình 7a ?
b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài) : widehat{A_1}+widehat{B}_1+widehat{C}_1+widehat{D}_1?
c) Có nhận xét gì về tổng các góc ngoài của tứ giác ?
Đọc tiếp
Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác
a) Tính các góc ngoài của tứ giác ở hình 7a ?
b) Tính tổng các góc ngoài của tứ giác ở hình 7b (tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài) : \(\widehat{A_1}+\widehat{B}_1+\widehat{C}_1+\widehat{D}_1=?\)
c) Có nhận xét gì về tổng các góc ngoài của tứ giác ?
Bài giải:
a) Góc ngoài còn lại: 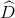 =3600 – (750 + 900 + 1200) = 750
=3600 – (750 + 900 + 1200) = 750
Ta tính được các góc ngoài tại các đỉnh A, B, C, D lần lượt là:
1050, 900, 600, 1050
b)Hình 7b SGK:
Tổng các góc trong  +
+  +
+ +
+ =3600
=3600
Nên tổng các góc ngoài
 +
+  +
+ +
+ =(1800 -
=(1800 -  ) + (1800 -
) + (1800 -  ) + (1800 -
) + (1800 -  ) + (1800 -
) + (1800 -  )
)
=(1800.4 - ( 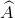 +
+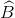 +
+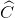 +
+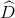 )
)
=7200 – 3600 =3600
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng 3600
Đúng 0
Bình luận (0)
Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\Leftrightarrow\widehat{D}=360^o-\left(\widehat{A}+\widehat{B}+\widehat{C}\right)\)
\(\Leftrightarrow\widehat{D}=360^o-\left(90^o+120^o+75^o\right)\)
\(\Leftrightarrow\widehat{D}=360^o-285^o=75^o\)
Ta có:+)\(\widehat{BAD}+\widehat{A_1}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{A_1}=180^o-\widehat{BAD}\)
\(\Rightarrow\widehat{A_1}=180^o-75^o=105^o\)
+)\(\widehat{B}_1+\widehat{CBA}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{B_1}=180^o-\widehat{CBA}\)
\(\Rightarrow\widehat{B_1}=180^o-90^0=90^o\)
\(+)\widehat{C_1}+\widehat{BCD}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{C_1}=180^o-\widehat{BCD}\)
\(\Rightarrow\widehat{C_1}=180^o-120^o=60^o\)
\(+)\widehat{D_1}+\widehat{ADC}=180^o\) (hai góc kề bù)
\(\Rightarrow\widehat{D}_1=180^o-\widehat{ADC}\)
\(\Rightarrow\widehat{D_1}=180^o-75^o=105^o\)
b,Xét tứ giác ABCD có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}+\widehat{D_1}\)
\(=\left(180^o-\widehat{A}\right)+\left(180^o-\widehat{B}\right)+\left(180^o-\widehat{C}\right)+\left(180^o-\widehat{D}\right)\)
\(=180^o.4-\left(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\right)\)
\(=720^o-360^o=360^o\)
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng \(360^o\)
Đúng 0
Bình luận (0)
a)
\(\widehat{A_1}=180^0-75^0=105^0\)|(kề bù)
\(\widehat{B_1}=180^0-90^0=90^0\)(kề bù)
\(\widehat{C_1}=180^0-120^0=60^0\)(kề bù)
\(\Rightarrow\widehat{D}=360^0-\left(\widehat{B_1}+\widehat{C_1}+\widehat{A_1}\right)\)
\(\widehat{D}=360^0-\left(90^0+120^0+75^0\right)\)
\(\leftrightarrow\widehat{D}=75^0\)
\(\Rightarrow\widehat{D_1}=180^0-75^0=105^0\)
b)Xét tứ giác ABCD (hình 7b) có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)
Nên tổng các góc ngoài là:
\(\widehat{A}_1+\widehat{B}_1+\widehat{C}_1+\widehat{D}_1=\left(180^0-\widehat{A}\right)+\left(180^0-\widehat{B}\right)+\left(180^0-\widehat{C}\right)+\left(180^0-\widehat{D}\right)\)
\(\Rightarrow180^0.4-\left(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}\right)\)
\(\Leftrightarrow\widehat{A}_1+\widehat{B}_1+\widehat{C}_1+\widehat{D}_1=720^0-360^0\)
\(\Rightarrow\widehat{A}_1+\widehat{B}_1+\widehat{C}_1+\widehat{D}_1=360^0\)
c) Nhận xét: Tổng các góc ngoài của tứ giác bằng \(360^0\)
Đúng 0
Bình luận (0)
Tam giác ABC có AB 5cm, BC 6cm và AC 7 cm. Gọi widehat{A}_1,widehat{B}_1,widehat{C}_1 theo thứ tự là góc ngoài tại đỉnh A, B, C của tam giác đó. Trong các khẳng định sau, khẳng định nào đúng ?
(A) widehat{A}_1widehat{B}_1widehat{C}_1 (B) widehat{B}_1widehat{C}_1widehat{A}_1
(C) widehat{C}_1widehat{A}_1widehat{B}_1 (D) widehat{C}_1widehat{B}_1widehat{A}_1
Đọc tiếp
Tam giác ABC có AB = 5cm, BC = 6cm và AC = 7 cm. Gọi \(\widehat{A}_1,\widehat{B}_1,\widehat{C}_1\) theo thứ tự là góc ngoài tại đỉnh A, B, C của tam giác đó. Trong các khẳng định sau, khẳng định nào đúng ?
(A) \(\widehat{A}_1>\widehat{B}_1>\widehat{C}_1\) (B) \(\widehat{B}_1>\widehat{C}_1>\widehat{A}_1\)
(C) \(\widehat{C}_1>\widehat{A}_1>\widehat{B}_1\) (D) \(\widehat{C}_1>\widehat{B}_1>\widehat{A}_1\)
BÀI 1 : CHO TỨ GIÁC ABCD CÓ : widehat{A}+widehat{B}200^{^0};widehat{B}+widehat{C}218^0;widehat{C}+widehat{D}160^0 TÍNH widehat{C}VÀ widehat{D}BÀI 2 : CHO TỨ GIÁC ABCD CÓ widehat{B}80^0;widehat{D}120^0GÓC NGOÀI ĐỈNH C BẰNG 1300 . TÍNH GÓC A CỦA TỨ GIÁC BÀI 3 : TỨ GIÁC ABCD CÓ widehat{A}57^0;widehat{C}110^0;widehat{D}75^0.TÍNH GÓC NGOÀI TẠI ĐỈNH B
Đọc tiếp
BÀI 1 : CHO TỨ GIÁC ABCD CÓ : \(\widehat{A}+\widehat{B}=200^{^0};\widehat{B}+\widehat{C}=218^0;\widehat{C}+\widehat{D}=160^0\) TÍNH \(\widehat{C}\)VÀ \(\widehat{D}\)
BÀI 2 : CHO TỨ GIÁC ABCD CÓ \(\widehat{B}=80^0;\widehat{D}=120^0\)GÓC NGOÀI ĐỈNH C BẰNG 1300 . TÍNH GÓC A CỦA TỨ GIÁC
BÀI 3 : TỨ GIÁC ABCD CÓ \(\widehat{A}=57^0;\widehat{C}=110^0;\widehat{D}=75^0\).TÍNH GÓC NGOÀI TẠI ĐỈNH B
Cho tam giác ABC biết \(a=7cm,b=23cm;\widehat{C}=130^0\). Tính \(c,\widehat{A,}\widehat{B}\) ?
Áp dụng định lý cô sin trong tam giác ABC:
\(c^2=a^2+b^2-2abcosC=7^2+23^2-2.7.23.cos130\)\(\cong784cm\).
Vậy \(c=28cm.\)
\(cosA=\dfrac{c^2+b^2-a^2}{2bc}=\dfrac{28^2+23^2-7^2}{2.23.28}=\dfrac{158}{161}\).
\(\Rightarrow\widehat{A}\cong11^o\).
\(\widehat{B}=180^o-\left(\widehat{A}+\widehat{C}\right)=180^o-\left(130^o+11^o\right)=39^o\).
Đúng 0
Bình luận (0)
1. Cho hình vẽ . Biết widehat{A} 135( độ ) , widehat{B} 45( độ ) , widehat{D} 55( độ )a) Đường thẳng a có song song với đường b không ? Vì sao ? b) Tính số đo góc C_1
Đọc tiếp
1. Cho hình vẽ . Biết \(\widehat{A}\) = 135'( độ ) , \(\widehat{B}\) = 45'( độ ) , \(\widehat{D}\) = 55'( độ )
a) Đường thẳng a có song song với đường b không ? Vì sao ?
b) Tính số đo góc C\(_1\)
a) A + B = 180 độ
Mà A và B là cặp góc trong cùng phía
=> a//b
b) a//b
=> D = C (so le trong)
=> C = 55 độ
Đúng 0
Bình luận (0)
Cho hình vẽ . Biết widehat{A} 147( độ ) , widehat{B} 33( độ ) , widehat{D} 59( độ )a) Đường thẳng a có song song vưới đường thẳng b không ? Vì sao ?b) Tính số đo góc C _1 ?
Đọc tiếp
Cho hình vẽ . Biết \(\widehat{A}\) = 147'( độ ) , \(\widehat{B}\) = 33'( độ ) , \(\widehat{D}\) = 59'( độ )
a) Đường thẳng a có song song vưới đường thẳng b không ? Vì sao ?
b) Tính số đo góc C \(_1\) ?
\(\widehat{D1}=\widehat{C1}\left(soletrong\right)\)
\(\widehat{A1}+\widehat{B1}=180^o\left(bùnhau\right)\)
\(\Rightarrow\)a//b
\(\widehat{D1}=\widehat{C1}\left(soletrong\right)=59^o\)
Đúng 0
Bình luận (0)
Cho Hình 16, biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc \(\widehat {{B_2}}\)
b) Tính số đo các góc \(\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}\)
c) Tính số đo các góc \(\widehat {{B_1}},\widehat {{A_1}}\).
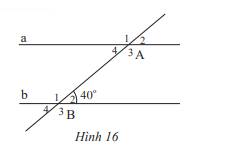
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)
Đúng 1
Bình luận (0)
Hình 41 cho biết d // d' // d" và hai góc \(60^0,100^0\). Tính các góc \(\widehat{E}_1,\widehat{G_2},\widehat{G}_3,\widehat{D}_4,\widehat{A}_5,\widehat{B}_6\) ?

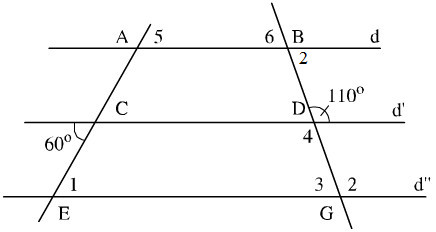
Xem hình vẽ. Có thể tính bằng nhiều cách, chẳng hạn:
+Vì d’ //d’’ có: \(\widehat{E}_1\) và góc 600 là hai góc so le trong nên \(\widehat{E}_1\)= 600
+Vì d’ // d’’ có: \(\widehat{G}_2\)và góc 1100 là hai góc đồng vị nên \(\widehat{G_2}\) = 1100
+ \(\widehat{G}_2\)+\(\widehat{G}_3\)=\(180^0\) (hai góc kề bù)
Nên \(\widehat{G_3}=180^0-\widehat{G}_2=180^0-110^0=70^0\)
+) \(\widehat{D}_4\)1100 (vì là hai góc đối đỉnh)
+) \(\widehat{A}_5\) = \(\widehat{A}_1\) (Hai góc đối đỉnh)
Mà \(\widehat{A}_1\)= 600 (vì là hai góc đồng vị)
Nên \(\widehat{A}_5\) = 600 .
+ \(\widehat{B}_6\) = \(\widehat{B}_2\)(vì là hai góc đối đỉnh)
Mà \(\widehat{B}_2\) + 1100 = 1800 (hai góc trong cùng phía)
Nên \(\widehat{B}_2\) = 1800 - 1100 = 700.
Do đó: \(\widehat{B}_6\) = 700
Đúng 0
Bình luận (0)
a) Năm cặp đường thẳng vuông góc là:
d3 ⊥ d4; d3 ⊥ d5; d3 ⊥ d7; d1 ⊥ d8; d1 ⊥ d2
b) Bốn cặp đường thẳng song song là: d4//d5; d5//d7; d4//d7; d8//d2
Đúng 0
Bình luận (0)
1) Tính góc ∠E1
Ta có d’//d” (gt)
⇒ ∠C = ∠E1 ( So le trong)
⇒ ∠E1 = 600 vì ∠C = 600
2) Tính ∠G3
Ta có d’//d”
⇒ ∠G2 = ∠D (Đồng vị)
⇒ ∠G1 = 1100
3) Tính ∠G3
Vì ∠G2 + ∠G3 = 1800 (kề bù)
⇒ ∠G3 = 700
4) Tính ∠D4
∠D4 = ∠D (Đối đỉnh)
⇒ ∠D4 = 1100
5) Tính ∠A5
Ta có d//d”
⇒ ∠A5 = ∠ E1 (Đồng vị)
⇒ ∠A5 = 600
6) Tính ∠B6
Ta có d//d”
⇒ ∠B6 = ∠G3 (Đồng vị)
⇒ ∠B6 = 700
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) Cho widehat{xOy} 100^0 Vẽ tia Oz sao cho widehat{zOy} 35^0 . Tính widehat{xOz} ?b) Trên đoạn thẳng AB lấy 2013 điểm khác nhau đặt theo thứ tự từ A đến B là : A,A_1,A_2,A_3,A_4,................,A_{2011},B. Từ điểm M không nằm trên đoạn thẳng AB , ta nối M vớiA,A_1,A_2,A_3,A_4,................,A_{2011},B. Tính số tam giác được tạo thành.
Đọc tiếp
a) Cho \(\widehat{xOy}\) \(=100^0\) Vẽ tia Oz sao cho \(\widehat{zOy}\) \(=35^0\) . Tính \(\widehat{xOz}\) ?
b) Trên đoạn thẳng AB lấy 2013 điểm khác nhau đặt theo thứ tự từ A đến B là : \(A,A_1,A_2,A_3,A_4,................,A_{2011},B.\) Từ điểm M không nằm trên đoạn thẳng AB , ta nối M với\(A,A_1,A_2,A_3,A_4,................,A_{2011},B.\) Tính số tam giác được tạo thành.
\(\widehat{xOz}+\widehat{zOy}=\widehat{xOy}\\\widehat{xOz}+35^o=100^o\\ \widehat{xOy}=100^o-35^o\\ \widehat{xOy}=65^o \)
Đúng 0
Bình luận (0)




















