Bài 1: Tứ giác.

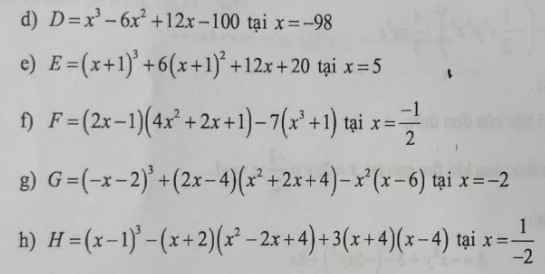
d: \(D=x^3-6x^2+12x-100\)

\(=x^3-6x^2+12x-8-92\)

\(=\left(x-2\right)^3-92\)

Khi x=-98 thì \(D=\left(-98-2\right)^3-92=-1000000-92=-1000092\)

e: \(E=\left(x+1\right)^3+6\left(x+1\right)^2+12x+20\)

\(=\left(x+1\right)^3+6\left(x+1\right)^2+12\left(x+1\right)+8\)

\(=\left(x+1+2\right)^3\)

\(=\left(x+3\right)^3\)

Khi x=5 thì \(E=\left(5+3\right)^3=8^3=512\)

f: \(F=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)

\(=\left(2x\right)^3-1^3-7x^3-7\)

\(=x^3-8\)

Khi x=-1/2 thì \(F=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)

g: \(G=\left(-x-2\right)^3+\left(2x-4\right)\left(x^2+2x+4\right)-x^2\left(x-6\right)\)

\(=-\left(x+2\right)^3+2\left(x-2\right)\left(x^2+2x+4\right)-x^3+6x^2\)

\(=-x^3-6x^2-12x-8+2\left(x^3-8\right)-x^3+6x^2\)

\(=-2x^3-12x-8+2x^3-16=-12x-24\)

Khi x=-2 thì \(G=-12\cdot\left(-2\right)-24=24-24=0\)

h: \(H=\left(x-1\right)^3-\left(x+2\right)\left(x^2-2x+4\right)+3\left(x+4\right)\left(x-4\right)\)

\(=x^3-3x^2+3x-1-\left(x^3+8\right)+3\left(x^2-16\right)\)

\(=x^3-3x^2+3x-1-x^3-8+3x^2-48\)

\(=3x-57\)

Khi x=-1/2 thì \(H=3\cdot\dfrac{-1}{2}-57=-1,5-57=-58,5\)

Ta có: MQ//BD

NP//BD

Do đó: MQ//NP

Ta có: MN//AC

\(Q,P\in AC\)

Do đó: MN//PQ

Xét tứ giác MNPQ có

MQ//NP

MN//PQ

Do đó: MNPQ là hình bình hành

e: \(E=-x\left(x-y\right)^2+\left(x-y\right)^3+y^2\left(y-2x\right)\)

\(=\left(x-y\right)^2\left(-x+x-y\right)+y^2\left(y-2x\right)\)

\(=\left(x-y\right)^2\cdot\left(-y\right)+y^2\cdot\left(y-2x\right)\)

\(=y\left[-\left(x-y\right)^2+y\left(y-2x\right)\right]\)

\(=y\left[-x^2+2xy-y^2+y^2-2xy\right]\)

\(=-x^2y\)

|2x-1|=1

=>\(\left[{}\begin{matrix}2x-1=1\\2x-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\)

TH1: x=1 và y=-2

=>\(E=-1^2\cdot\left(-2\right)=1\cdot2=2\)

TH2: x=0 và y=-2

=>\(E=-0^2\cdot\left(-2\right)=0\)

f: \(F=-\left(2x-y\right)^3-x\left(2x-y\right)^2-y^3\)

\(=-\left(2x-y\right)^2\left[2x-y+x\right]-y^3\)

\(=\left(-2x-y\right)^2\cdot\left(3x-y\right)-y^3\)

\(\left(x-2\right)^2>=0\forall x;y^2>=0\forall y\)

Do đó: \(\left(x-2\right)^2+y^2>=0\forall x,y\)

Dấu '=' xảy ra khi x-2=0 và y=0

=>x=2 và y=0

Khi x=2 và y=0 thì \(F=\left(-2\cdot2-0\right)^2\cdot\left(3\cdot2-0\right)-0^3\)

\(=\left(-4\right)^2\cdot6=96\)

g: \(G=\left(x+y\right)\left(x^2-xy+y^2\right)+3\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)

\(=x^3+y^3+3\left(8x^3-y^3\right)\)

\(=x^3+y^3+24x^3-3y^3=25x^3-2y^3\)

x+y=2

=>x-3=2

=>x=5

Thay x=5 và y=-3 vào G, ta được:

\(G=25\cdot5^3-2\left(-3\right)^3=3179\)

h: \(H=\left(x+3y\right)\left(x^2-3xy+9y^2\right)+\left(3x-y\right)\left(9x^2+3xy+y^2\right)\)

\(=x^3+\left(3y\right)^3+\left(3x\right)^3-y^3\)

\(=x^3+27y^3+27x^3-y^3\)

\(=28x^3+26y^3\)

3x-y=5

=>3*2-y=5

=>y=6-5=1

Thay x=2 và y=1 vào H, ta được:

\(H=28\cdot2^3+26\cdot1^3=250\)

Giúp tui điii:3

a: Ta có: ΔBAC cân tại B

mà BI là đường cao

nên I là trung điểm của AC

Xét tứ giác BICD có

H là trung điểm chung của BC và ID

=>BICD là hình bình hành

Hình bình hành BICD có \(\widehat{BIC}=90^0\)

nên BICD là hình chữ nhật

b: Ta có: ΔBDC vuông tại D

=>\(BD^2+DC^2=BC^2\)

=>\(BD^2=14^2-10^2=96\)

=>\(BD=4\sqrt{6}\left(cm\right)\)

Vì BDCI là hình chữ nhật

nên \(S_{BDCI}=BD\cdot DC=4\sqrt{6}\cdot10=40\sqrt{6}\left(cm^2\right)\)

c: Để hình chữ nhật BDCI là hình vuông thì BI=CI

mà CI=CA/2

nên BI=CA/2

Xét ΔBAC có

BI là đường trung tuyến

\(BI=\dfrac{AC}{2}\)

Do đó: ΔBAC vuông tại B

=>\(\widehat{ABC}=90^0\)

Sửa đề: MN=MP

a: Xét tứ giác ANBP có

M là trung điểm chung của AB và NP

=>ANBP là hình bình hành

b: Ta có: ANBP là hình bình hành

=>AP//NB và AP=NB

Ta có: AP//NB

N\(\in\)BC

Do đó: AP//NC

Ta có: AP=NB

NB=NC

Do đó: AP=NC

Xét tứ giác APNC có

AP//NC

AP=NC

Do đó: APNC là hình bình hành

=>AC=NP

Tia đối của MN có điểm P thì $NP>MN$ bạn nhé. Bạn xem lại đề.

a: Xét tứ giác ADHE có

\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)

=>ADHE là hình chữ nhật

b: ΔHDB vuông tại D

mà DI là đường trung tuyến

nên IH=ID=IB

=>IH=ID

=>ΔIHD cân tại I

=>\(\widehat{IDH}=\widehat{IHD}\)

mà \(\widehat{IHD}=\widehat{BCA}\)(hai góc đồng vị, HD//AC)

nên \(\widehat{IDH}=\widehat{BCA}\)

Ta có: ADHE là hình chữ nhật

=>\(\widehat{EDH}=\widehat{EAH}=\widehat{HAC}\)

mà \(\widehat{HAC}=\widehat{ABC}\left(=90^0-\widehat{HAB}\right)\)

nên \(\widehat{EDH}=\widehat{ABC}\)

\(\widehat{EDI}=\widehat{EDH}+\widehat{IDH}\)

\(=\widehat{ABC}+\widehat{ACB}\)

\(=90^0\)

=>ED\(\perp\)DI

c: Ta có: ΔCEH vuông tại E

mà EK là đường trung tuyến

nên KE=KH

=>ΔKEH cân tại K

=>\(\widehat{KEH}=\widehat{KHE}\)

mà \(\widehat{KHE}=\widehat{ABC}\)(hai góc đồng vị, EH//AB)

nên \(\widehat{KEH}=\widehat{ABC}\)

Ta có: ADHE là hình chữ nhật

=>\(\widehat{DEH}=\widehat{DAH}\)

mà \(\widehat{DAH}=\widehat{ACB}\left(=90^0-\widehat{ABC}\right)\)

nên \(\widehat{DEH}=\widehat{ACB}\)

\(\widehat{KED}=\widehat{KEH}+\widehat{DEH}\)

\(=\widehat{ABC}+\widehat{ACB}=90^0\)

=>KE\(\perp\)ED

mà DI\(\perp\)DE

nên DI//KE

Xét tứ giác EKID có DI//EK

nên EKID là hình thang

Hình thang EKID có \(\widehat{KED}=90^0\)

nên EKID là hình thang vuông

d: DI=HB/2

=>HB=2*DI=2(cm)

EK=1/2CH

=>\(CH=2\cdot EK=2\cdot4=8\left(cm\right)\)

BC=BH+CH

=2+8

=10(cm)

Xét ΔABC có AH là đường cao

nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot10\cdot6=30\left(cm^2\right)\)

TH1: ABCD không phải là hình thoi hoặc hình vuông

Gọi BM,DN lần lượt là phân giác của \(\widehat{ABC};\widehat{ADC}\)

Xét tứ giác ABCD có

\(\widehat{BAD}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360^0\)

=>\(2\cdot\left(\widehat{NBM}+\widehat{NDM}\right)=360^0-\widehat{A}-\widehat{C}=360^0-2\cdot\widehat{C}\)

=>\(\widehat{NBM}+\widehat{NDM}=180^0-\widehat{C}\)(1)

Xét ΔCMB có

\(\widehat{C}+\widehat{CMB}+\widehat{CBM}=180^0\)

=>\(\widehat{CMB}+\widehat{NBM}=180^0-\widehat{C}\)(2)

Từ (1) và (2) suy ra \(\widehat{NDM}=\widehat{CMB}\)

mà hai góc này ở vị trí đồng vị

nên BM//DN (ĐPCM)

TH2: ABCD là hình thoi hoặc hình vuông

ABCD là hình thoi

=>BD là tia phân giác của \(\widehat{ABC}\) và DB là tia phân giác của \(\widehat{ADC}\)

=>Các đường phân giác của góc B và góc D trùng nhau