Bài 1: Tứ giác.
Nội dung lý thuyết
1. Định nghĩa
Định nghĩa: Tứ giác \(ABCD\) là hình gồm bốn đoạn thẳng \(AB,BC,CD,DA\), trong đó bất kì hai đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
Ví dụ: Mỗi hình sau đây là một tứ giác:


Hình 4 sau đây không là một tứ giác, vì các cạnh \(BC,CD\) cùng nằm trên một đường thẳng:

Với các tứ giác trong hình 1, 2, 3, thay vì gọi tên là tứ giác \(ABCD\), ta cũng có thể gọi là tứ giác \(BCDA,BADC,CBAD,...\) Các điểm \(A,B,C,D\) được gọi là các đỉnh, còn \(AB,BC,CD,DA\) là các cạnh.
Lưu ý: Khi gọi tên tứ giác, ta cần đảm bảo thứ tự liên tiếp của các đỉnh. (Ví dụ: Không gọi là tứ giác \(ACBD\)).
Trong 3 tứ giác trong các hình 1, 2, 3 ta thấy: Chỉ có tứ giác \(ABCD\) trong hình 1 thỏa mãn tính chất: Nó luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào trong 4 cạnh \(AB,BC,CD,DA\). Các tứ giác \(ABCD\) trong hình 2 và hình 3 không thỏa mãn tính chất này.
(Thật vậy: Tứ giác \(ABCD\) trong hình 2 nằm về hai phía của đường thẳng chứa cạnh \(BC\); Tứ giác \(ABCD\) trong hình 3 nằm về hai phía của đường thẳng chứa cạnh \(AD\).)
Ta nói tứ giác \(ABCD\) trong hình 1 là một tứ giác lồi.
Định nghĩa: Tứ giác lồi là tứ giác luôn nằm trên một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác.
Chú ý: Từ nay, nếu chỉ nói tứ giác mà không nói gì thêm, ta hiểu đó là tứ giác lồi.
Xét hình vẽ sau:

Hình 5 cho ta hình ảnh của tứ giác \(ABCD\) và các điểm \(M,N,P,Q\), trong đó:
- Hai đỉnh kề nhau là: \(A\) và \(B\), \(B\) và \(C\), \(C\) và \(D\), \(D\) và \(A\).
- Hai đỉnh đối nhau là: \(A\) và \(C\), \(B\) và \(D\).
- Đường chéo (đoạn thẳng nối hai đỉnh đối nhau) là: \(AC,BD\).
- Hai cạnh kề nhau là: \(AB\) và \(BC\), \(BC\) và \(CD\), \(CD\) và \(DA\), \(DA\) và \(AB\).
- Hai cạnh đối nhau là: \(AB\) và \(CD\), \(AD\) và \(BC\).
- Góc: \(\widehat{A},\widehat{B},\widehat{C},\widehat{D}\). Trong đó hai góc đối nhau là \(\widehat{A}\) và \(\widehat{C}\), \(\widehat{B}\) và \(\widehat{D}\).
- Điểm nằm trong tứ giác (điểm trong của tứ giác) là: \(M,P\).
- Điểm nằm ngoài tứ giác (điểm ngoài của tứ giác) là: \(N,Q\).@579549@
2. Tổng các góc trong tứ giác
Ở lớp dưới ta đã biết: Tổng các góc trong một tam giác bằng \(180^0.\)
Bây giờ, dùng định lí này, ta chứng minh được định lí sau đây:
Định lí: Tổng các góc của một tứ giác bằng \(360^0.\)
Thật vậy:
Xét tứ giác \(ABCD\) (hình vẽ):
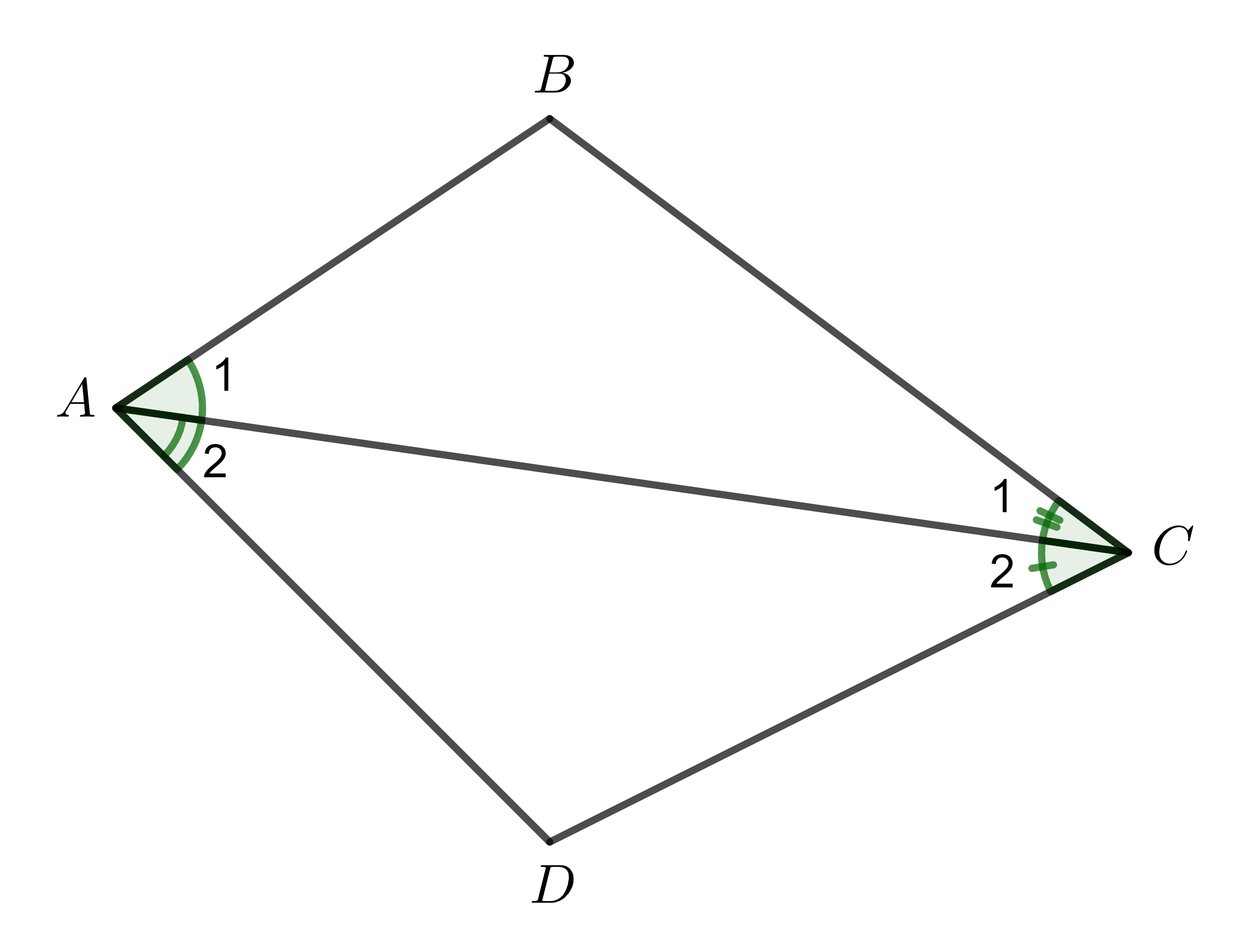
Áp dụng định lí tổng 3 góc trong tam giác:
Với tam giác \(ABC\): \(\widehat{A_1}+\widehat{B}+\widehat{C_1}=180^0\).
Với tam giác \(ADC\): \(\widehat{A_2}+\widehat{D}+\widehat{C_2}=180^0\).
\(\Rightarrow\widehat{BAC}+\widehat{B}+\widehat{BCD}+\widehat{D}=\left(\widehat{A_1}+\widehat{B}+\widehat{C_1}\right)+\left(\widehat{A_2}+\widehat{D}+\widehat{C_2}\right)=180^0+180^0=360^0\)
Như vậy, xét tứ giác \(ABCD\) ta có: \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\).
Kết quả này không phụ thuộc vào việc chọn tứ giác \(ABCD\). Như vậy, định lí được chứng minh.
Áp dụng:
a) Cho tứ giác \(ABCD\) có \(\widehat{A}=120^0;\widehat{C}=40^0;\widehat{D}=100^0\). Tính góc \(\widehat{B}\)?
b) Cho tứ giác \(ABCD\) có \(\widehat{A}+\widehat{C}=240^0\). Tìm tổng hai góc ngoài tại hai đỉnh \(B\) và \(D\)?
Lời giải:
a) Xét tứ giác \(ABCD\). Theo định lí tổng các góc trong tứ giác, ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\) \(\Rightarrow\widehat{B}=360^0-\left(\widehat{A}+\widehat{B}+\widehat{C}\right)=360^0-\left(120^0+40^0+100^0\right)=100^0.\)
b) Áp dụng định lí tổng các góc trong tứ giác với tứ giác \(ABCD\) ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\) \(\Rightarrow\widehat{B}+\widehat{D}=360^0-\left(\widehat{A}+\widehat{C}\right)=360^0-240^0=120^0.\)
Gọi \(\widehat{B'},\widehat{D'}\) lần lượt là góc ngoài đỉnh \(B,D\) của tứ giác \(ABCD\).
Ta có: \(\widehat{B'}+\widehat{D'}=\left(180^0-\widehat{B}\right)+\left(180^0-\widehat{D}\right)=2.180^0-\left(\widehat{B}+\widehat{D}\right)=360^0-120^0=240^0.\)
@580380@