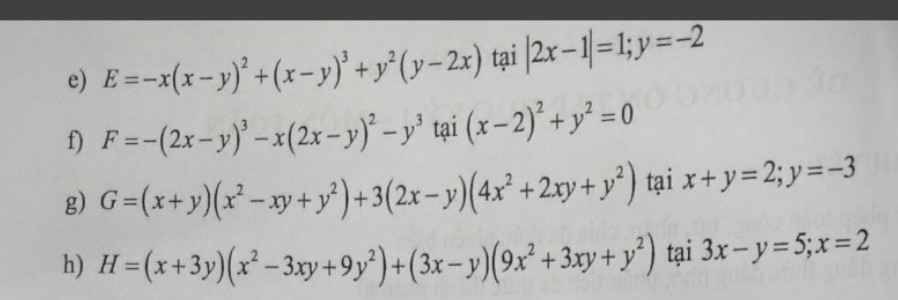e: \(E=-x\left(x-y\right)^2+\left(x-y\right)^3+y^2\left(y-2x\right)\)
\(=\left(x-y\right)^2\left(-x+x-y\right)+y^2\left(y-2x\right)\)
\(=\left(x-y\right)^2\cdot\left(-y\right)+y^2\cdot\left(y-2x\right)\)
\(=y\left[-\left(x-y\right)^2+y\left(y-2x\right)\right]\)
\(=y\left[-x^2+2xy-y^2+y^2-2xy\right]\)
\(=-x^2y\)
|2x-1|=1
=>\(\left[{}\begin{matrix}2x-1=1\\2x-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\)
TH1: x=1 và y=-2
=>\(E=-1^2\cdot\left(-2\right)=1\cdot2=2\)
TH2: x=0 và y=-2
=>\(E=-0^2\cdot\left(-2\right)=0\)
f: \(F=-\left(2x-y\right)^3-x\left(2x-y\right)^2-y^3\)
\(=-\left(2x-y\right)^2\left[2x-y+x\right]-y^3\)
\(=\left(-2x-y\right)^2\cdot\left(3x-y\right)-y^3\)
\(\left(x-2\right)^2>=0\forall x;y^2>=0\forall y\)
Do đó: \(\left(x-2\right)^2+y^2>=0\forall x,y\)
Dấu '=' xảy ra khi x-2=0 và y=0
=>x=2 và y=0
Khi x=2 và y=0 thì \(F=\left(-2\cdot2-0\right)^2\cdot\left(3\cdot2-0\right)-0^3\)
\(=\left(-4\right)^2\cdot6=96\)
g: \(G=\left(x+y\right)\left(x^2-xy+y^2\right)+3\left(2x-y\right)\left(4x^2+2xy+y^2\right)\)
\(=x^3+y^3+3\left(8x^3-y^3\right)\)
\(=x^3+y^3+24x^3-3y^3=25x^3-2y^3\)
x+y=2
=>x-3=2
=>x=5
Thay x=5 và y=-3 vào G, ta được:
\(G=25\cdot5^3-2\left(-3\right)^3=3179\)
h: \(H=\left(x+3y\right)\left(x^2-3xy+9y^2\right)+\left(3x-y\right)\left(9x^2+3xy+y^2\right)\)
\(=x^3+\left(3y\right)^3+\left(3x\right)^3-y^3\)
\(=x^3+27y^3+27x^3-y^3\)
\(=28x^3+26y^3\)
3x-y=5
=>3*2-y=5
=>y=6-5=1
Thay x=2 và y=1 vào H, ta được:
\(H=28\cdot2^3+26\cdot1^3=250\)