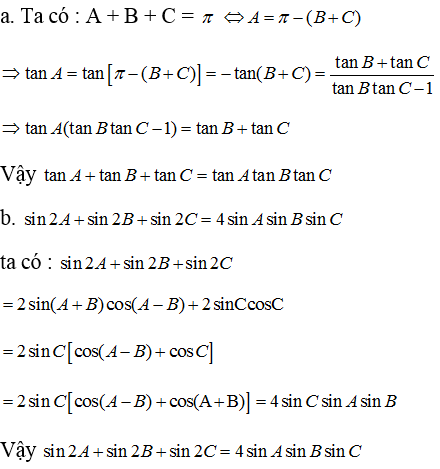Chứng minh rằng :
sin2A+sin2B+sin2C=4sinA.sinB.sinC
Nhờ mọi người CM giùm tôi bài này nhé

Những câu hỏi liên quan
Chứng minh rằng trong tam giác ABC, ta có:
a. tanA + tanB + tanC = tanAtanBtanC 
b. sin2A + sin2B + sin2C = 4sinAsinBsinC
Vì A, B, C là ba góc của tam giác nên ta có : A + B + C = π.
⇒ C = π - (A + B); A + B = π - C
a) Ta có: tan A + tan B + tan C = (tan A + tan B) + tan C
= tan (A + B). (1 – tan A.tan B) + tan C
= tan (π – C).(1 – tan A. tan B) + tan C
= -tan C.(1 – tan A. tan B) + tan C
= -tan C + tan A. tan B. tan C + tan C
= tan A. tan B. tan C
b) sin 2A + sin 2B + sin 2C
= 2. sin (A + B). cos (A – B) + 2.sin C. cos C
= 2. sin (π – C). cos (A – B) + 2.sin C. cos (π – (A + B))
= 2.sin C. cos (A – B) - 2.sin C. cos (A + B)
= 2.sin C.[cos (A – B) - cos (A + B)]
= 2.sin C.[-2sinA. sin(- B)]
= 2.sin C. 2.sin A. sin B ( vì sin(- B)= - sinB )
= 4. sin A. sin B. sin C
Đúng 0
Bình luận (1)
Các góc của tam giác ABC thỏa mãn hệ thức, \(\frac{sinB+sinC}{sinA}=\frac{sin2B+sin2C}{sin2A}\)
Chứng minh rằng cosB+cosC=1
Chứng minh đẳng thức sin2A+sin2B+sin2C=4sinA.sinB.sinC với A,B,C là 3 góc trong tam giác ABC
Lời giải:
Ta có:
$\sin 2A+\sin 2B=2\sin \frac{2A+2B}{2}\cos \frac{2A-2B}{2}=2\sin (A+B)\cos (A-B)$
$=2\sin (\pi -C)\cos (A-B)=2\sin C\cos (A-B) $
Do đó:
$\sin 2A+\sin 2B+\sin 2C=\sin 2C+2\sin C\cos (A-B)=2\sin C\cos C+2\sin C\cos (A-B)$
$=2\sin C[\cos C+\cos (A-B)]=2\sin C[\cos (\pi -A-B)+\cos (A-B)]$
$=2\sin C[\cos (A-B)-\cos (A+B)]=-2.\sin C[\cos (A+B)-\cos (A-B)]$
$=-2\sin C. (-2).\sin \frac{(A+B)+(A-B)}{2}.\sin \frac{(A+B)-(A-B)}{2}=4\sin C.\sin A.\sin B$
Ta có đpcm.
trong tam giác ABC ta có
sin2A + sin2B + sin2C = 4.sinA.sinB.sinC
\(sin2A+sin2B+sin2C=2sin\left(A+B\right).cos\left(A-B\right)+2sinC.cosC\)
\(=2sinC.cos\left(A-B\right)+2sinC.cosC=2sinC\left[cos\left(A-B\right)+cosC\right]\)
\(=4sinC.cos\left(\frac{A+C-B}{2}\right).cos\left(\frac{A-B-C}{2}\right)\)
\(=4sinC.cos\left(\frac{\pi-2B}{2}\right).cos\left(\frac{2A-\pi}{2}\right)=4sinC.cos\left(\frac{\pi-2B}{2}\right).cos\left(\frac{\pi-2A}{2}\right)\)
\(=4sinC.cos\left(\frac{\pi}{2}-B\right).cos\left(\frac{\pi}{2}-A\right)\)
\(=4sinA.sinB.sinC\)
Đúng 0
Bình luận (0)
Cho A, B, C là 3 góc 1 tam giác. Chứng minh
a) \(cos2A+cos2B+cos2C=-1-4cosA.cosB.cosC\)
b) \(sin2A+sin2B+sin2C=4.sinA.sinB.sinC\)
\(cos2A+cos2B+cos2C=2cos\left(A+B\right).cos\left(A-B\right)+2cos^2C-1\)
\(=-2cosC.cos\left(A-B\right)+2cos^2C-1\)
\(=-2cosC\left[cos\left(A-B\right)-cosC\right]-1\)
\(=-2cosC\left[cos\left(A-B\right)+cos\left(A+B\right)\right]-1\)
\(=-4cosC.cosA.cosB-1\)
\(sin2A+sin2B+sin2C=2sin\left(A+B\right)cos\left(A-B\right)+2sinC.cosC\)
\(=2sinC.cos\left(A-B\right)+2sinC.cosC\)
\(=2sinC\left[cos\left(A-B\right)+cosC\right]=2sinC\left[cos\left(A-B\right)-cos\left(A+B\right)\right]\)
\(=-4sinC.sinA.sin\left(-B\right)=4sinA.sinB.sinC\)
Đúng 0
Bình luận (0)
1. Cho A,B,C là ba góc của tam giác ABC. Chứng minh rằng:
sin2A+sin2B+sin2C= 4sinA.sinB.sinC
2. viết pt đường tròn (C) tiếp xúc với hai đường thẳng d1: 3x +2y +3=0 và d2: 2x-3y+15=0 và có tâm nằm trên đường thằng d3: x-y=0
Cho \(\Delta ABC\), chứng minh rằng:
a) \(\tan A+\tan B+\tan C=\tan A\tan B\tan C\)(\(\widehat{A},\widehat{B},\widehat{C}\)cùng khác \(\frac{\pi}{2}\))
b) \(\sin2A+\sin2B+\sin2C=4\sin A\sin B\sin C\)
cho A , B , C là 3 góc của tam giác ABC . chứng minh rằng : a) sin2A + sin2B + sin2C = 4sinAsinBsinC ; b) cosA + cosB + cosC = 1 = 4sin\(\frac{A}{2}\)sin\(\frac{B}{2}\)sin\(\frac{C}{2}\) ; c) cos2A + cos2B + cos2C = 1 - 2cosAcosBcosC
Chứng minh rằng trong một tam giác ABC ta có :
a) \(\tan A+\tan B+\tan C=\tan A\tan B\tan C\) (\(\widehat{A},\widehat{B},\widehat{C}\) cùng khác \(\dfrac{\pi}{2}\))
b) \(\sin2A+\sin2B+\sin2C=4\sin A.\sin B.\sin C\)