Cm: (1-sinx) (1+sinx) = sin2x.cot2x

Những câu hỏi liên quan
CM đẳng thức : \(\dfrac{1+sinx}{1-sinx} + \dfrac{1-sinx}{1+sinx}\) = 2(1+2tan2x)
Lời giải:
Ta có:
\(\frac{1+\sin x}{1-\sin x}+\frac{1-\sin x}{1+\sin x}=\frac{(1+\sin x)^2+(1-\sin x)^2}{(1-\sin x)(1+\sin x)}\)
\(=\frac{1+\sin ^2x+2\sin x+1-2\sin x+\sin ^2x}{1-\sin ^2x}\)
\(=\frac{2(1+\sin ^2x)}{\cos ^2x}=\frac{2(\sin ^2x+\cos ^2x+\sin ^2x)}{\cos ^2x}\)
\(=\frac{4\sin ^2x+2\cos ^2x}{\cos ^2x}=4(\frac{\sin x}{\cos x})^2+2=4\tan ^2x+2=2(1+2\tan ^2x)\)
Ta có đpcm.
Đúng 0
Bình luận (0)
CM \(\left(\frac{\sqrt{1+sinx}}{\sqrt{1-sinx}}-\frac{\sqrt{1-sinx}}{\sqrt{1+sinx}}\right)^2\) = \(4tan^2x\)
ĐK: ...
\(VT=\left[\frac{\left(1+sinx\right)-\left(1-sinx\right)}{\sqrt{1-sin^2x}}\right]^2=\left(\frac{2sinx}{cosx}\right)^2=4tan^2x=VP\left(đpcm\right)\)
Cho x nhọn. CM các đẳng thức sau:
\(\frac{sinx+cosx-1}{1-cosx}\) = \(\frac{2.cosx}{sinx-cosx+1}\)
\(\frac{cosx}{sinx-cosx}\) + \(\frac{sinx}{sinx+cosx}\) = \(\frac{1+cot^2x}{1-cot^2x}\)
xem câu đầu ở đây nè https://olm.vn/hoi-dap/question/1248282.html
Đúng 0
Bình luận (0)
Cm đẳng thức sau: Mn giúp mình bài này với ^^
\(\dfrac{sinx}{sinx-cosx}-\dfrac{cosx}{sinx+cosx}=\dfrac{1+cot^2x}{1-cot^2x}\)
\(VT=\dfrac{\sin x}{\sin x-cosx}-\dfrac{cosx}{sinx+cosx}\\ =\dfrac{sin^2x+\sin x\cos x-\sin x\cos x+\cos^2x}{\left(\sin x-\cos x\right)\left(\sin x+\cos x\right)}\\ =\dfrac{1}{\sin^2x-\cos^2x}\)
\(VP=\dfrac{1+\cot^2x}{1-\cot^2}\\ =\left(1+\cot^2x\right)\cdot\dfrac{1}{1-\cot^2x} \\=\dfrac{1}{\sin^2x}\cdot\dfrac{1}{1-\cot^2x}\\ =\dfrac{1}{\sin^2x-\sin^2x\cdot\cot^2x}\\ =\dfrac{1}{\sin^2x-\cos^2x}=VT\)
Đúng 0
Bình luận (0)
\(\sqrt{\dfrac{1+sinx}{1-sinx}}+\sqrt{\dfrac{1-sinx}{1+sinx}}=?\) (sao cho gọn nhất)
\(=\dfrac{1+sinx+1-sinx}{\sqrt{\left(1-sinx\right)\left(1+sinx\right)}}=\dfrac{2}{\sqrt{1-sin^2x}}=\dfrac{2}{\sqrt{cos^2x}}=\dfrac{2}{\left|cosx\right|}\)
Đúng 3
Bình luận (0)
Giải các phương trình sau:
a, \(\dfrac{Sin^2x+Sinx}{Sinx-1}=-2\)
b,\(\dfrac{Cos2x+Sinx}{Sinx-1}+1=0\)
a)Đk:\(sinx\ne1\)
Pt\(\Leftrightarrow sin^2x+sinx=-2\left(sinx-1\right)\)
\(\Leftrightarrow sin^2x+3sinx-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{-3+\sqrt{17}}{2}\left(tm\right)\\sinx=\dfrac{-3-\sqrt{17}}{2}\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=arcc.sin\left(\dfrac{-3+\sqrt{17}}{2}\right)+k2\pi\\x=\pi-arc.sin\left(\dfrac{-3+\sqrt{17}}{2}\right)+k2\pi\end{matrix}\right.\)(\(k\in Z\))
b)Đk:\(sinx\ne1\)
Pt \(\Leftrightarrow\dfrac{1-2sin^2x+sinx}{sinx-1}+1=0\)
\(\Leftrightarrow\dfrac{-\left(sinx-1\right)\left(2sinx+1\right)}{sinx-1}+1=0\)
\(\Leftrightarrow-\left(2sinx+1\right)+1=0\)
\(\Leftrightarrow sinx=0\) (tm)
\(\Leftrightarrow x=k\pi,k\in Z\)
Vậy...
Đúng 1
Bình luận (0)
Rút gọn \(\sqrt{\frac{1+sinx}{1-sinx}}+\sqrt{\frac{1-sinx}{1+sinx}}\)
\(\sqrt{\frac{1+sinx}{1-sinx}}+\sqrt{\frac{1-sinx}{1+sinx}}=\sqrt{\frac{sin^2\frac{x}{2}+cos^2\frac{x}{2}+2sin\frac{x}{2}.cos\frac{x}{2}}{sin^2\frac{x}{2}+cos^2\frac{x}{2}-2sin\frac{x}{2}.cos\frac{x}{2}}}+\sqrt{\frac{sin^2\frac{x}{2}+cos^2\frac{x}{2}-2sin\frac{x}{2}.cos\frac{x}{2}}{sin^2\frac{x}{2}+cos^2\frac{x}{2}+2sin\frac{x}{2}.cos\frac{x}{2}}}\)
\(=\sqrt{\frac{\left(sin\frac{x}{2}+cos\frac{x}{2}\right)^2}{\left(sin\frac{x}{2}-cos\frac{x}{2}\right)^2}}+\sqrt{\frac{\left(sin\frac{x}{2}-cos\frac{x}{2}\right)^2}{\left(sin\frac{x}{2}+cos\frac{x}{2}\right)^2}}=\frac{\left|sin\frac{x}{2}+cos\frac{x}{2}\right|}{\left|sin\frac{x}{2}-cos\frac{x}{2}\right|}+\frac{\left|sin\frac{x}{2}-cos\frac{x}{2}\right|}{\left|sin\frac{x}{2}+cos\frac{x}{2}\right|}\)
\(=\frac{\left(sin\frac{x}{2}+cos\frac{x}{2}\right)^2+\left(sin\frac{x}{2}-cos\frac{x}{2}\right)^2}{\left|sin^2\frac{x}{2}-cos^2\frac{x}{2}\right|}=\frac{2}{\left|cosx\right|}\)
Đúng 0
Bình luận (0)
1, Tìm txd của hàm số sau
a, y = \(\sqrt{sinx-1}\)
b, y =\(\sqrt{\dfrac{1-sinx}{1+sinx}}\)
c, y = \(\dfrac{1+cosx}{sinx}\)
ĐKXĐ: (tất cả \(k\in Z\))
a. \(sinx-1\ge0\Leftrightarrow sinx\ge1\)
\(\Leftrightarrow sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b. \(\left\{{}\begin{matrix}\dfrac{1-sinx}{1+sinx}\ge0\left(luôn-đúng\right)\\1+sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow sinx\ne-1\)
\(\Leftrightarrow x\ne-\dfrac{\pi}{2}+k2\pi\)
c. \(sinx\ne0\Leftrightarrow x\ne k\pi\)
Đúng 1
Bình luận (0)
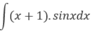 bằng:
bằng:
A. (x + 1)cosx + sinx + C B. -(x + 1)cosx + sinx + C
C. -(x + 1)sinx + cosx + C D. (x + 1)cosx - sinx + C
Đáp án: B.
Hướng dẫn: Đặt u = (x + 1), v' = sinx.
Đúng 0
Bình luận (0)




















