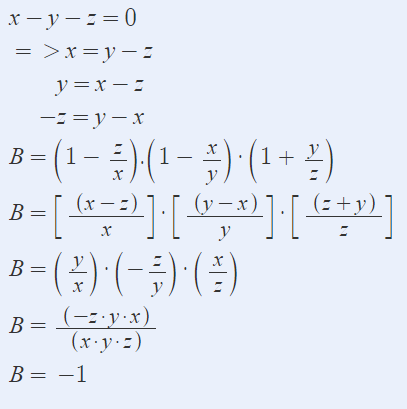Cho 1/x+1/y+1/z = 0
Tính A = x/y+y/z+z/x

Những câu hỏi liên quan
Cho x,y,z ko bằng 0 và x-y-z=0
Tính giá trị biểu thức: B= (1-z/x).)(1-x/y).(1+y/z)+2023
x-y-z=0
=>x=y+z và y=x-z và z=x-y
B=(1-z/x)(1-x/y)(1+y/z)+2023
\(=\dfrac{x-z}{x}\cdot\dfrac{y-x}{y}\cdot\dfrac{y+z}{z}+2023\)
\(=\dfrac{y}{x}\cdot\dfrac{-z}{y}\cdot\dfrac{x}{z}+2023=2023-1=2022\)
Đúng 0
Bình luận (0)
Cho x, y, z ≠ 0 và x-y-z=0
Tính GTBT B=\(\left(1-\dfrac{z}{x}\right).\left(1-\dfrac{x}{y}\right).\left(1+\dfrac{y}{z}\right)\)
Ta có: \(x-y-z=0\)
\(\Rightarrow x-y=z\)
\(x-z=y\)
\(y+z=x\)
\(\Rightarrow B=\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\)
\(=\dfrac{x-z}{x}.\dfrac{-\left(y-x\right)}{y}.\dfrac{z+y}{z}\)
\(=\dfrac{y}{x}.-\dfrac{z}{y}.\dfrac{z}{x}=-1\)
\(\Rightarrow B=-1\)
Đúng 2
Bình luận (0)
cho x,y,z khác 0 và x-y-z = 0
Tính giá trị biểu thức B= \(\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\)
Cho x y z đôi một khác nhau và 1 x 1 y 1 z 0Tính giá trị A yz x 2 2yz xz y 2 2xz xy z 2 2xy
tao đẹp trai thì có gì sai
bài này mà là âm nhạc???
Cho biết các số x,y,z thỏa mãn :
x2+2y+1=0
y2+2z+1=0
z2+2x+1=0
Tính giá trị biểu thức:
a) A = x2020 + y2020+z2020
b) B=\(\dfrac{1}{x^{2022}}+\dfrac{1}{y^{2022}}+\dfrac{1}{z^{2022}}\)
Ta có: \(\left\{{}\begin{matrix}x^2+2y+1=0\\y^2+2z+1=0\\z^2+2x+1=0\end{matrix}\right.\)
\(\Rightarrow x^2+2y+1+y^2+2z+1+z^2+2x+1=0\)
\(\Rightarrow\left(x+1\right)^2+\left(y+1\right)^2+\left(z+1\right)^2=0\)
\(\Rightarrow x=y=z=-1\)(do \(\left(x+1\right)^2,\left(y+1\right)^2,\left(z+1\right)^2\ge0\forall x,y,z\))
a) \(A=x^{2020}+y^{2020}+z^{2020}=\left(-1\right)^{2020}+\left(-1\right)^{2020}+\left(-1\right)^{2020}=1+1+1=3\)
b) \(B=\dfrac{1}{x^{2020}}+\dfrac{1}{y^{2020}}+\dfrac{1}{z^{2020}}=\dfrac{1}{\left(-1\right)^{2020}}+\dfrac{1}{\left(-1\right)^{2020}}+\dfrac{1}{\left(-1\right)^{2020}}=\dfrac{1}{1}+\dfrac{1}{1}+\dfrac{1}{1}=3\)
Đúng 2
Bình luận (0)
cho x+y+z=0
Tính GTBT: xy/(x^2+y^2-z^2)+yz/(y^2+z^2-x^2)+zx/(z^2+x^2-y^2)
\(x+y+z=0\\ \Rightarrow\left\{{}\begin{matrix}x=-y-z\\y=-z-x\\z=-x-y\end{matrix}\right.\)
\(\dfrac{xy}{x^2+y^2-z^2}+\dfrac{yz}{y^2+z^2-x^2}+\dfrac{zx}{z^2+x^2-y^2}\)
\(=\dfrac{xy}{x^2+y^2-\left(-x-y\right)^2}+\dfrac{yz}{y^2+z^2-\left(-y-z\right)^2}+\dfrac{zx}{z^2+x^2-\left(-z-x\right)^2}\)
\(=\dfrac{xy}{x^2+y^2-\left(x+y\right)^2}+\dfrac{yz}{y^2+z^2-\left(y+z\right)^2}+\dfrac{zx}{z^2+x^2-\left(z+x\right)^2}\)
\(=\dfrac{xy}{x^2+y^2-x^2-2xy-y^2}+\dfrac{yz}{y^2+z^2-y^2-2yz-z^2}+\dfrac{zx}{z^2+x^2-z^2-2zx-x^2}\)
\(=\dfrac{xy}{-2xy}+\dfrac{yz}{-2yz}+\dfrac{zx}{-2zx}\)
\(=-\dfrac{1}{2}-\dfrac{1}{2}-\dfrac{1}{2}\)
\(=-\dfrac{3}{2}\)
Đúng 2
Bình luận (0)
Cho x,y,z đoio một khác nhau thỏa mãn x+y+z=0
Tính \(P=\dfrac{2022\left(x-y\right)\left(y-z\right)\left(z-x\right)}{2xy^2+2yz^2+2zx^2+3xyz}\)
Đúng 2
Bình luận (0)
cho \(\dfrac{x}{a}\)+\(\dfrac{b}{y}\)+\(\dfrac{z}{c}\)=3 và \(\dfrac{a}{x}\)+\(\dfrac{b}{y}\)+\(\dfrac{c}{z}\)=0
tính K= \(\dfrac{x^2}{a^2}\)+\(\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}\)
cho x/y+z+1 = y/z+1+x = z/1+x+y = 1/x+y+z. CMR biểu thức sau có giá trị nguyên: A = x+y/z+1 = y+z/1+x = z+1/x+y = 1+x/y+z
\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1và\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=0tính\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}\)
vì \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1=>\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}+2\left(\frac{xy}{ab}+\frac{yz}{bc}+\frac{xz}{cz}\right)=1\)
==>A=\(1-2\left(\frac{xy}{ab}+\frac{yz}{bc}+\frac{xz}{cz}\right)=1-\frac{2\left(cxy+ayz+bzx\right)}{xyz}\)(1)
mặt khác từ \(\frac{a}{x}+\frac{b}{y}+\frac{c}{z}=0\) ==> \(\frac{ayz+bzx+cxy}{xyz}=0=>ayz+cxy+bzx=0\) ( thay vào (1) ta có
A=1-0=1
Đúng 0
Bình luận (0)