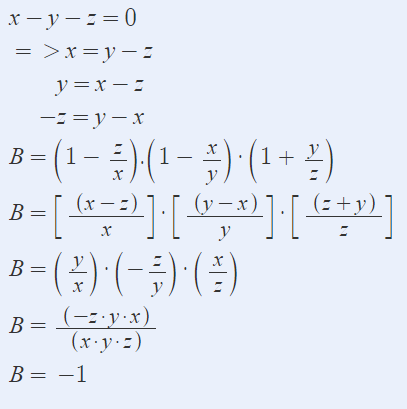Các câu hỏi tương tự
Cho \(x;y;z\ne0\) và x - y - z = 0. Tính giá trị biểu thức:
\(B=\left(1-\dfrac{z}{x}\right)\left(1-\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\)
4 tháng 12 2021 lúc 16:37
Bài 1: Cho dfrac{3a+b+2c}{2a+c}dfrac{a+3b+c}{2b}dfrac{a+2b+2c}{b+c}. Tính giá trị biểu thức Adfrac{left(a+bright)left(b+cright)left(c+aright)}{abc}Bài 2: Cho x; y; z ≠ 0 và dfrac{x+3y-z}{z}dfrac{y+3x-x}{x}dfrac{z+3x-y}{y}. Tính Pleft(dfrac{x}{y}+3right)left(dfrac{y}{z}+3right)left(dfrac{z}{x}+3right) Cứu tui với :
Đọc tiếp
Bài 1: Cho \(\dfrac{3a+b+2c}{2a+c}=\dfrac{a+3b+c}{2b}=\dfrac{a+2b+2c}{b+c}\). Tính giá trị biểu thức A=\(\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}\)
Bài 2: Cho x; y; z ≠ 0 và \(\dfrac{x+3y-z}{z}=\dfrac{y+3x-x}{x}=\dfrac{z+3x-y}{y}\). Tính P=\(\left(\dfrac{x}{y}+3\right)\left(\dfrac{y}{z}+3\right)\left(\dfrac{z}{x}+3\right)\)
Cứu tui với :<
4 tháng 12 2021 lúc 12:43
Bài 1: Cho dfrac{3a+b+2c}{2a+c}dfrac{a+3b+c}{2b}dfrac{a+2b+2c}{b+c}. Tính giá trị biểu thức Adfrac{left(a+bright)left(b+cright)left(c+aright)}{abc}Bài 2: Cho x; y; z ≠ 0 và dfrac{x+3y-z}{z}dfrac{y+3x-x}{x}dfrac{z+3x-y}{y}. Tính Pleft(dfrac{x}{y}+3right)left(dfrac{y}{z}+3right)left(dfrac{z}{x}+3right)
Đọc tiếp
Bài 1: Cho \(\dfrac{3a+b+2c}{2a+c}=\dfrac{a+3b+c}{2b}=\dfrac{a+2b+2c}{b+c}\). Tính giá trị biểu thức A=\(\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}\)
Bài 2: Cho x; y; z ≠ 0 và \(\dfrac{x+3y-z}{z}=\dfrac{y+3x-x}{x}=\dfrac{z+3x-y}{y}\). Tính P=\(\left(\dfrac{x}{y}+3\right)\left(\dfrac{y}{z}+3\right)\left(\dfrac{z}{x}+3\right)\)
4 tháng 12 2021 lúc 14:53
Bài 1: Cho dfrac{3a+b+2c}{2a+c}dfrac{a+3b+c}{2b}dfrac{a+2b+2c}{b+c}. Tính giá trị biểu thức Adfrac{left(a+bright)left(b+cright)left(c+aright)}{abc}Bài 2: Cho x; y; z ≠ 0 và dfrac{x+3y-z}{z}dfrac{y+3x-x}{x}dfrac{z+3x-y}{y}. Tính Pleft(dfrac{x}{y}+3right)left(dfrac{y}{z}+3right)left(dfrac{z}{x}+3right)
Đọc tiếp
Bài 1: Cho \(\dfrac{3a+b+2c}{2a+c}=\dfrac{a+3b+c}{2b}=\dfrac{a+2b+2c}{b+c}\). Tính giá trị biểu thức A=\(\dfrac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}\)
Bài 2: Cho x; y; z ≠ 0 và \(\dfrac{x+3y-z}{z}=\dfrac{y+3x-x}{x}=\dfrac{z+3x-y}{y}\). Tính P=\(\left(\dfrac{x}{y}+3\right)\left(\dfrac{y}{z}+3\right)\left(\dfrac{z}{x}+3\right)\)
cho 3 số x,y,z đôi 1 khác nhau và chứng minh rằng :
\(\dfrac{y-z}{\left(x-y\right)\cdot\left(x-z\right)}+\dfrac{z-x}{\left(y-z\right)\cdot\left(y-x\right)}+\dfrac{y-x}{\left(z-x\right)\cdot\left(z-y\right)}=\dfrac{2}{x-y}+\dfrac{2}{y-z}+\dfrac{2}{z-x}\)
25 tháng 10 2021 lúc 21:22
cho x,y,z là các số thực khác, thỏa mãn:
\(\dfrac{x+y-2017z}{z}=\dfrac{y+z-2017x}{x}=\dfrac{z+x-2017y}{y}\)
tính gtbt: \(P=\left(1+\dfrac{y}{x}\right)\left(1+\dfrac{x}{z}\right)\left(1+\dfrac{z}{y}\right)\)
Cho x,y,z khác 0 và x-y-z=0. TÍnh giá trị của biểu thức B=\(\left(1-\frac{z}{x}\right)\left(1-\frac{x}{y}\right)\left(1+\frac{y}{z}\right)\)
Cho x, y, z khác 0 và x - y - z = 0. Tính giá trị biểu thức \(A=\left(1-\frac{z}{x}\right)\left(1-\frac{x}{y}\right)\left(1+\frac{y}{z}\right)\)
Cho x,y,z khác 0 và x-y-z = 0
Tính giá trị của biểu thức \(M=\left(1-\frac{z}{x}\right)\left(1-\frac{x}{y}\right)\left(1+\frac{y}{z}\right)\)