x2 -2(m-1)-x+m2-3m+4
Tìm hệ thức giữa x1và x2 độc lập với m
Giúp mình với,mình đang cần gấp ạ>>>>
Cho phương trình x 2 - 2 ( m - 1 ) x + m 2 - 3 m = 0 Giả sử phương trình có hai nghiệm x 1 ; x 2 .Tìm hệ thức giữa x 1 ; x 2 độc lập đối với m.
![]()
![]()
![]()
![]()
Đáp án: A
Theo hệ thức Vi-ét ta có: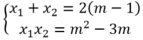
Ta xét các phương án:
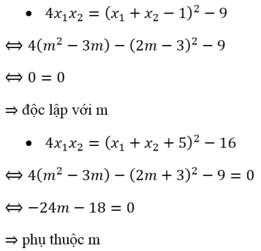
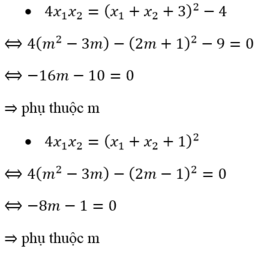
Mọi người giúp mình với, mình đang cần gấp ;(((
Hãy chứng minh: y=(m2-3m)x2+(2m2+m)x+3 là hàm số bậc nhất với m có giá trị là bao nhiêu?
Hàm số bậc nhất \(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m=0\\2m^2+m\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\left(m-3\right)=0\\m\left(2m+1\right)\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m=0\\m=3\end{matrix}\right.\\\left\{{}\begin{matrix}m\ne0\\m\ne-\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m=3\)
Cho pt x^2 - 2 (m-1)x+2m-3=0 gọi x1 x2 là 2 nghiệm của pt tìm hệ thức liên hệ giữa x1 x2 độc lập với m
X4-2.(m+2)x2+m2-2m+3=0
Định m để phương trình có 4 nghiệm
Tìm hệ thức độc lập với m
Tìm E=x1.x2.x3.x4 theo m .Tính GTNN của E
Đặt \(t=x^2\left(t\ge0\right)\)
Khi đó phương trình ban đầu tương đương với pt\(t^2-2\left(m+2\right)t+m^2-2m+3=0\) (*)
Để pt ban đầu có 4 nghiệm phân biệt thì pt (*) có hai nghiệm dương phân biệt ⇔
\(\left\{{}\begin{matrix}\Delta>0\\S>0\\P>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m+2\right)^2-m^2+2m-3>0\\2\left(m+2\right)>0\\m^2-2m+3>0\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}6m+1>0\\m+2>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-\dfrac{1}{6}\\m>-2\end{matrix}\right.\)
⇔ \(m>-\dfrac{1}{6}.\)
Giả sử (*) có hai nghiệm là t1, t2. Khi đó theo Viet ta có t1.t2 = m2 - 2m + 3.
Ta có: x1.x2.x3.x4 = t1.t2 = m2 - 2m +3.
Ta có E = m2 - 2m + 3 = (m - 1)2 + 2 ≥ 2.
Min E = 2. Dấu bằng xảy ra khi m = 1.
cho pt x\(^2\) - 2(m - 1)x - 2m + 5 = 0.
a,giả sử pt có 2 nghiệm x1,x2 . hãy tìm 1 hệ thức liên hệ giữa x1, x2 độc lập với m
b, tính theo m biểu thức A =\(\frac{1}{x1+1}+\frac{1}{x2+1}\)
c, tìm m để A=2
Mn giúp e với ạ. em đg cần gấp
Help me :(
câu a bạn áp dụng hệ thức Viet rồi rút m và thay vào cái kia r tìm ra thôi
![]()
\(\Delta'=\left(m-1\right)^2-4\left(-2m+5\right)=m^2+6m-19\ge0\)
Theo định lý Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-2\\x_1x_2=-2m+5\end{matrix}\right.\)
Cộng vế với vế: \(x_1+x_2+x_1x_2=3\)
Đây là biểu thức liên hệ 2 nghiệm ko phụ thuộc m
b/ \(A=\frac{1}{x_1+1}+\frac{1}{x_2+1}=\frac{x_1+x_2+2}{\left(x_1+1\right)\left(x_2+1\right)}=\frac{x_1+x_2+2}{x_1x_2+x_1+x_2+1}\)
\(=\frac{2m-2+2}{3+1}=\frac{2m}{4}=\frac{m}{2}\) (mẫu số sử dụng kết quả câu a để rút gọn cho lẹ)
c/ \(A=2\Rightarrow\frac{m}{2}=2\Rightarrow m=4\)
Thay vào biểu thức \(\Delta\) thấy thỏa mãn.
Vậy \(m=4\)
Tìm GTNN của biêu thức D=(x+1).(x2 - 4).(x+5)+2014
giúp mình với ạ, mình đang cần gấp!
Lời giải:
$D=(x+1)(x^2-4)(x+5)+2014$
$=(x+1)(x+2)(x-2)(x+5)+2014$
$=(x^2+3x+2)(x^2+3x-10)+2014$
$=t(t-12)+2014$ (đặt $x^2+3x+2=t$)
$=t^2-12t+2014=(t-6)^2+1978$
$=(x^2+3x-4)^2+1978\geq 1978$
Vậy gtnn của biểu thức là $1978$. Giá trị này đạt tại $x^2+3x-4=0$
$\Leftrightarrow x=1$ hoặc $x=-4$
cho phương trình x^2-2(m-1)x+m^2+m=0 a tìm m để phương trình có 2 nghiệm phân biệt b khi có 2 nghiệm x1 x2 tìm hệ thức giữa x1 x2 độc lập đối với m
\(\Delta'=\left(m-1\right)^2-\left(m^2+m\right)=-3m+1>0\Rightarrow m< \dfrac{1}{3}\)
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2+m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{x_1+x_2+2}{2}\\x_1x_2=m^2+m\end{matrix}\right.\)
\(\Rightarrow x_1x_2=\left(\dfrac{x_1+x_2+2}{2}\right)^2+\dfrac{x_1+x_2+2}{2}\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m (bạn có thể rút gọn thêm nếu cần)
cho phương trình:
\(\left(m-2\right)x^2-2\left(m-1\right)x+m-3=0\)
Thiết lập hệ thức giữa x1, x2 độc lập với m.
(Em làm hoài không mất được m xin được chỉ giáo ạ:(
Coi như pt đã cho có nghiệm, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-1\right)}{m-2}\\x_1x_2=\dfrac{m-3}{m-2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m-2+1\right)}{m-2}=2+\dfrac{2}{m-2}\\x_1x_2=\dfrac{m-2-1}{m-2}=1-\dfrac{1}{m-2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=2+\dfrac{2}{m-2}\\2x_1x_2=2-\dfrac{2}{m-2}\end{matrix}\right.\)
Cộng vế:
\(\Rightarrow x_1+x_2+2x_1x_2=4\)
Đây là hệ thức liên hệ ko phụ thuộc m
Coi như pt đã cho có nghiệm, theo hệ thức Viet: ⇒⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩x1+x2=2(m−2+1)m−2=2+2m−2x1x2=m−2−1m−2=1−1m−2⇒{�1+�2=2(�−2+1)�−2=2+2�−2�1�2=�−2−1�−2=1−1�−2
Cho biết pt \(x^2-\left(m-2\right)x+\left(2m-1\right)=0\) có các nghiệm x1 ; x2 .
Lập một hệ thức giữa x1 ; x2 độc lập đối với m.
Theo viet: \(x_1+x_2=m+2\)
\(x_1x_2=2m-1\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x_1+2x_2=2m+4\\x_1x_2=2m-1\end{matrix}\right.\)
Trừ vế cho vế: \(2x_1+2x_2-x_1x_2=5\)
Vậy hệ thức trên độc lập với m.