Đáp án: A
Theo hệ thức Vi-ét ta có: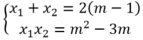
Ta xét các phương án:
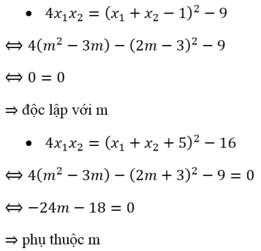
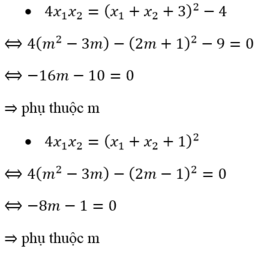
Đáp án: A
Theo hệ thức Vi-ét ta có: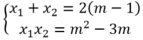
Ta xét các phương án:
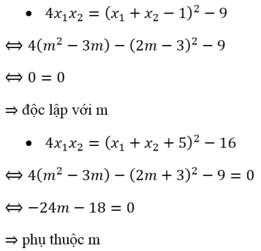
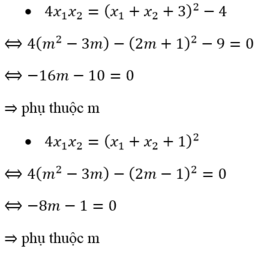
Cho hệ phương trình: m x + 3 m − 2 y + m − 3 = 0 2 x + m + 1 y − 4 = 0 . Hệ thức liên hệ giữa x và y độc lập đối với tham số m khi hệ phương trình có nghiệm duy nhất là:
A. x = − 1 + 15 6 y
B. y = − 1 − 15 6 x
C. x = − 1 − 15 6 y
D. y = − 1 + 15 6 x
Cho hệ phương trình
\(\hept{\begin{cases}mx-x+y=m\\2x+my=1\end{cases}}\)
Khi hệ có nghiệm duy nhất (x; ) y .Tìm hệ thức giữa x, y độc lập đối với m.
Giả sử phương trình bậc hai ẩn x (m là tham số): \(x^2-2\left(m-1\right)x-m^3+\left(m+1\right)^2=0\\ \)
có hai nghiệm x1,x2 thỏa mãn điều kiện \(x_1+x_2\le4\). Tìm giá trị lớn nhất và nhỏ nhất của biểu thức sau:
\(P=x^3_1+x_2^3+x_1x_2\left(3x_1+3x_2+8\right)\)
Cho hệ phương trình: m − 1 x + y = 3 m − 4 x + m − 1 y = m . Hệ thức liên hệ giữa x và y độc lập đối với tham số m khi hệ có nghiệm duy nhất là:
A. y = x – 2
B. y = x + 2
C. y = −x – 2
D. y = −x + 2
Cho f(x)=x^2 -2(m-2)x+m+10. Định m để:
a. Phương trình f(x)=0 có một nghiệm x= 1 và tính nghiệm kia
b. Phương trình f(x)=0 có nghiệm kép. Tính nghiệm kép đó.
c. Tìm m để phương trình f(x)=0 có 2 nghiệm âm phân biệt.
d. Tìm m để f(x)<0 có nghiệm đúng với mọi xϵR
giúp em câu b với
Cho phương trình \(mx^2+\left(2m-2\right)x+m-1=0\) ,(1) ( với m là tham số )
a) Định m để phương trình ( 1 ) có hai nghiệm phân biệt.
b) Gọi 1 2 x x; là hai nghiệm của phương trình ( 1 ). Chứng minh rằng giá trị biểu thức \(Q=\dfrac{1013}{x_1}+\dfrac{1013}{x_2}+1\) luôn là hằng số.
a)Định tham số m để phương trình (m-2)x^2-2(m-1)x+m=0 có hai nghiệm trai dấu
b)Tìm tất cả các giá trị của tham số m để bất phương trình (m-1)x^2+2(m-1)x+2≥ 0, ∀ x ∈ R
cho phương trình x2 -2(m+1)x + m-1=0
a) Tìm m để phương trình có hai nghiệm trái dấu
b) tìm m để phương trình có hai nghiệm trong đó một nghiệm bằng hai lần nghiệm còn lại
giúp mình với ạ. Mình cảm ơn
Cho hàm số F(x) = (m + 1)x2 - 2mx + m - 2 (m là tham số). a) Tìm m để phương trình f(x) = 0 có hai nghiệm trái dấu? b) Tìm m để bất phương trình f(x) < 0 có một nghiệm đúng với mọi x.