\(N=\dfrac{\left(ab\right)^3+\left(bc\right)^3+\left(ca\right)^3}{\left(ab\right)\left(bc\right)\left(ca\right)}\)

Đặt \(\left(ab;bc;ca\right)=\left(x;y;z\right)\Rightarrow x+y+z=0\Rightarrow N=\dfrac{x^3+y^3+z^3}{xyz}\)

\(N=\dfrac{x^3+y^3+z^3-3xyz+3xyz}{xyz}=\dfrac{\dfrac{1}{2}\left(x+y+z\right)\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]+3xyz}{xyz}=\dfrac{3xyz}{xyz}=3\)

Ta có: \(A=a\left(a^2-bc\right)+b\left(b^2-ac\right)+c\left(c^2-ab\right)=0\)

\(\Rightarrow A=a^3+b^3+c^3-3abc=0\) \(\Rightarrow A=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)

\(\Rightarrow A=\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)=0\)

\(\Rightarrow A=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)

Vì \(a+b+c\ne0\Rightarrow a^2+b^2+c^2-ab-ac-bc=0\)

Xét \(M=a^2+b^2+c^2-ab-ac-bc=0\)

\(\Rightarrow2M=2a^2+2b^2+2c^2-2ab-2ac-2bc=0\)

\(\Rightarrow2M=\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)

Vì \(\left(a-b\right)^2\ge0;\left(b-c\right)^2\ge0;\left(c-a\right)^2\ge0\forall a,b,c\)

\(\Rightarrow a-b=0;b-c=0;c-a=0\) \(\Rightarrow a=b=c\)

\(\Rightarrow P=\frac{a^2}{b^2}+\frac{b^2}{c^2}+\frac{c^2}{a^2}=1+1+1=3\) 

\(\)Ta có: \(a+b+c=0 \Rightarrow b+c=-a \Rightarrow (b+c)^2=(-a)^2 \Leftrightarrow b^2+c^2+2bc=a^2 \Leftrightarrow a^2-b^2-c^2=2bc\)

Tương tự: \(b^2-c^2-a^2=2ca;c^2-a^2-b^2=2ab\)

\(P=...=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ca}+\dfrac{c^2}{2bc}=\dfrac{a^3+b^3+c^3}{2abc}=\dfrac{3abc}{2abc}=\dfrac{3}{2}\)

----
Bổ đề \(a+b+c=0 \Leftrightarrow a^3+b^3+c^3\)

Ở đây ta c/m chiều thuận:
Với \(a+b+c=0 \Leftrightarrow a+b=-c \Rightarrow (a+b)^3=(-c)^3 \Leftrightarrow a^3+b^3+3ab(a+b)=-c^3 \Leftrightarrow a^3+b^3+c^3=3abc(QED)\)

\(\left(a+b+c\right)^2=a^2+b^2+c^2\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ac\right)=a^2+b^2+c^2\)

\(\Leftrightarrow2\left(ab+bc+ac\right)=0\Leftrightarrow ab+bc+ac=0\Leftrightarrow bc=-ab-ac\)

\(\dfrac{a^2}{a^2+2bc}=\dfrac{a^2}{a^2+bc-ac-ab}=\dfrac{a^2}{\left(a-c\right)\left(a-b\right)}\)

CMTT: \(\left\{{}\begin{matrix}\dfrac{b^2}{b^2+2ca}=\dfrac{b^2}{\left(b-a\right)\left(b-c\right)}\\\dfrac{c^2}{c^2+2ab}=\dfrac{c^2}{\left(c-a\right)\left(c-b\right)}=\dfrac{c^2}{\left(a-c\right)\left(b-c\right)}\end{matrix}\right.\)

\(\Rightarrow A=\dfrac{a^2}{\left(a-c\right)\left(a-b\right)}+\dfrac{b^2}{\left(b-a\right)\left(b-c\right)}+\dfrac{c^2}{\left(a-c\right)\left(b-c\right)}=\dfrac{a^2\left(b-c\right)-b^2\left(a-c\right)+c^2\left(a-b\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}=\dfrac{\left(a-b\right)\left(b-c\right)\left(a-c\right)}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}=1\)

\(\dfrac{ab}{a+b}=\dfrac{bc}{b+c}=\dfrac{ca}{c+a}\Rightarrow\dfrac{a+b}{ab}=\dfrac{b+c}{bc}=\dfrac{c+a}{ca}\)

\(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{c}+\dfrac{1}{a}\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{a}=\dfrac{1}{c}\\\dfrac{1}{a}=\dfrac{1}{b}\end{matrix}\right.\) \(\Rightarrow a=b=c\)

\(\Rightarrow M=\dfrac{a^2+a^2+a^2}{a^2+a^2+a^2}=1\)

Lời giải:

\(\frac{ab}{a+b}=\frac{bc}{b+c}=\frac{ca}{c+a}\Rightarrow \frac{abc}{c(a+b)}=\frac{abc}{a(b+c)}=\frac{bca}{b(c+a)}\)

\(\Leftrightarrow c(a+b)=a(b+c)=b(c+a)\)

\(\Leftrightarrow ac+bc=ab+ac=bc+ab\Leftrightarrow ab=bc=ac\)

\(\Rightarrow a=b=c\) (do $a,b,c>0$)

$\Rightarrow M=\frac{a^2+a^2+a^2}{a^2+a^2+a^2}=1$

Ta có:

\(a+b+c-abc=\left(a+b+c\right)\left(ab+bc+ca\right)-abc\)

\(=\left(a+b+c\right)\left(ab+c\left(a+b\right)\right)-abc\)

\(=\left(a+b\right)ab+\left(a+b\right)^2c+abc+c^2\left(a+b\right)-abc\)

\(=\left(a+b\right)\left(ab+c^2+c\left(a+b\right)\right)\)

\(=\left(a+b\right)\left(ab+ac+c^2+bc\right)\)

\(=\left(a+b\right)\left[a\left(b+c\right)+c\left(b+c\right)\right]\)

\(=\left(a+b\right)\left(b+c\right)\left(a+c\right)\)

Đồng thời:

\(a^2+1=a^2+ab+bc+ac=a\left(a+b\right)+c\left(a+b\right)=\left(a+b\right)\left(a+c\right)\)

Tương tự:

\(b^2+1=\left(a+b\right)\left(b+c\right)\)

\(c^2+1=\left(a+c\right)\left(b+c\right)\)

Từ đó:

\(P=\dfrac{\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2}{\left(a+b\right)\left(a+c\right)\left(a+b\right)\left(b+c\right)\left(a+c\right)\left(b+c\right)}\)

\(=\dfrac{\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2}{\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2}=1\)

Bài 1: Ta có:

\(M=\frac{ad}{abcd+abd+ad+d}+\frac{bad}{bcd.ad+bc.ad+bad+ad}+\frac{c.abd}{cda.abd+cd.abd+cabd+abd}+\frac{d}{dab+da+d+1}\)

\(=\frac{ad}{1+abd+ad+d}+\frac{bad}{d+1+bad+ad}+\frac{1}{ad+d+1+abd}+\frac{d}{dab+da+d+1}\)

$=\frac{ad+abd+1+d}{ad+abd+1+d}=1$

Bài 2:

Vì $a,b,c,d\in [0;1]$ nên

\(N\leq \frac{a}{abcd+1}+\frac{b}{abcd+1}+\frac{c}{abcd+1}+\frac{d}{abcd+1}=\frac{a+b+c+d}{abcd+1}\)

Ta cũng có:
$(a-1)(b-1)\geq 0\Rightarrow a+b\leq ab+1$

Tương tự:

$c+d\leq cd+1$

$(ab-1)(cd-1)\geq 0\Rightarrow ab+cd\leq abcd+1$

Cộng 3 BĐT trên lại và thu gọn thì $a+b+c+d\leq abcd+3$

$\Rightarrow N\leq \frac{abcd+3}{abcd+1}=\frac{3(abcd+1)-2abcd}{abcd+1}$

$=3-\frac{2abcd}{abcd+1}\leq 3$

Vậy $N_{\max}=3$

3.

Hình vẽ:

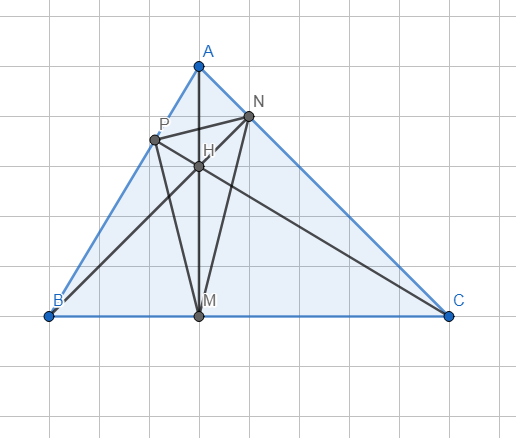
Lời giải:

a) △AMC và △BNC có: \(\widehat{AMC}=\widehat{BNC}=90^0;\widehat{ACB}\) là góc chung.

\(\Rightarrow\)△AMC∼△BNC (g-g).

\(\Rightarrow\dfrac{AC}{BC}=\dfrac{CM}{CN}\Rightarrow AC.CN=BC.CM\left(1\right)\)

b) △AMB và △CPB có: \(\widehat{AMB}=\widehat{CPB}=90^0;\widehat{ABC}\) là góc chung.

\(\Rightarrow\)△AMB∼△CPB (g-g)

\(\Rightarrow\dfrac{AB}{CB}=\dfrac{BM}{BP}\Rightarrow AB.BP=BC.BM\left(2\right)\)

Từ (1) và (2) suy ra:

\(AC.CN+AB.BP=BC.CM+BC.BM=BC.\left(CM+BM\right)=BC.BC=BC^2\left(đpcm\right)\)b) Gọi \(M_0\) là trung điểm BC, giả sử \(AB< AC\).

\(\widehat{HBM}=90^0-\widehat{BHM}=90^0-\widehat{AHN}=\widehat{CAM}\)

△HBM và △CAM có: \(\widehat{HBM}=\widehat{CAM};\widehat{HMB}=\widehat{CMA}=90^0\)

\(\Rightarrow\)△HBM∼△CAM (g-g) 

\(\Rightarrow\dfrac{MH}{CM}=\dfrac{BM}{MA}\Rightarrow MH.MA=BM.CM\)

Ta có: \(BM.CM=\left(BM_0-MM_0\right)\left(CM_0+MM_0\right)=\left(BM_0-MM_0\right)\left(BM_0+MM_0\right)=BM_0^2-MM_0^2\le BM_0^2=\dfrac{BC^2}{4}\)

\(\Rightarrow MH.MA\le\dfrac{BC^2}{4}\).

Vì \(BC\) không đổi nên: \(max\left(MH.MA\right)=\dfrac{BC^2}{4}\), đạt được khi △ABC cân tại A hay A nằm trên đường trung trực của BC.

c) Sửa đề: \(S_1.S_2.S_3\le\dfrac{1}{64}.S^3\)

△AMC∼△BNC \(\Rightarrow\dfrac{AC}{BC}=\dfrac{MC}{NC}\Rightarrow\dfrac{AC}{MC}=\dfrac{BC}{NC}\)

△ABC và △MNC có: \(\dfrac{AC}{MC}=\dfrac{BC}{NC};\widehat{ACB}\) là góc chung.

\(\Rightarrow\)△ABC∼△MNC (c-g-c)

\(\Rightarrow\dfrac{S_{MNC}}{S_{ABC}}=\dfrac{S_1}{S}=\dfrac{MC}{AC}.\dfrac{NC}{BC}\left(1\right)\)

Tương tự: 

△ABC∼△MBP \(\Rightarrow\dfrac{S_{MBP}}{S_{ABC}}=\dfrac{S_2}{S}=\dfrac{MB}{AB}.\dfrac{BP}{BC}\left(2\right)\)

△ABC∼△ANP \(\Rightarrow\dfrac{S_{ANP}}{S_{ABC}}=\dfrac{S_3}{S}=\dfrac{AN}{AB}.\dfrac{AP}{AC}\left(3\right)\)

Từ (1), (2), (3) suy ra:

\(\dfrac{S_1}{S}.\dfrac{S_2}{S}.\dfrac{S_3}{S}=\left(\dfrac{MC}{AC}.\dfrac{NC}{BC}\right).\left(\dfrac{MB}{AB}.\dfrac{BP}{BC}\right).\left(\dfrac{AN}{AB}.\dfrac{AP}{AC}\right)\) 

\(\Rightarrow\dfrac{S_1}{S}.\dfrac{S_2}{S}.\dfrac{S_3}{S}=\left(\dfrac{MC.MB}{AC.AB}\right).\left(\dfrac{BP.AP}{AC.BC}\right).\left(\dfrac{AN.CN}{AB.BC}\right)\) (*)

Áp dụng câu b) ta có:

\(\left\{{}\begin{matrix}BM.CM\le\dfrac{1}{4}BC^2\\AP.BP\le\dfrac{1}{4}AB^2\\AN.CN\le\dfrac{1}{4}AC^2\end{matrix}\right.\)

Từ (*) suy ra:

\(\dfrac{S_1}{S}.\dfrac{S_2}{S}.\dfrac{S_3}{S}\le\left(\dfrac{\dfrac{1}{4}BC^2}{AC.AB}\right).\left(\dfrac{\dfrac{1}{4}AC^2}{AC.BC}\right).\left(\dfrac{\dfrac{1}{4}AB^2}{AB.BC}\right)=\dfrac{1}{64}\)

\(\Rightarrow S_1.S_2.S_3\le\dfrac{1}{64}.S^3\)

Dấu "=" xảy ra khi △ABC đều.

Ta có kết quả tổng quát hơn như sau:

Cho $a,b,c \neq 0$ thỏa mãn $\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0.$

Chứng minh rằng $$S={\frac {k{a}^{2}-k-1}{{a}^{2}+2\,bc}}+{\frac {{b}^{2}k-k-1}{2\,ac+{b}^{2}}}+{\frac {{c}^{2}k-k-1}{2\,ab+{c}^{2}}}=k$$