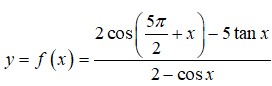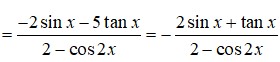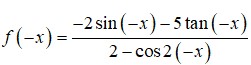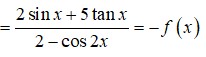\(\leftrightarrow2cos^2x+sinx=cosx+1\)

\(\leftrightarrow cos^2x-cosx-sin^2x+sinx=0\)

\(\leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx\right)-\left(cosx-sinx\right)=0\)

\(\leftrightarrow\left(cosx-sinx\right).\left(cosx+sinx-1\right)=0\)

\(cosx-sinx=0\leftrightarrow x=\frac{\pi}{4}+k\pi\left(k\epsilon Z\right)\)

\(cosx+sinx=1\leftrightarrow Sin\left(x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\leftrightarrow x=k2\pi hoacx=\frac{\pi}{2}+k2\pi\)

PT \(\Leftrightarrow-2\left(1-2.sin^2\dfrac{x}{2}\right)-\sqrt{3}.cos2x=-1+2\left(cosx.cos\dfrac{3\pi}{4}-sinx.sin\dfrac{3\pi}{4}\right)^2\)

\(\Leftrightarrow-2.cosx-\sqrt{3}.cos2x=-1+2\left(cosx.-\dfrac{\sqrt{2}}{2}-sinx.\dfrac{\sqrt{2}}{2}\right)^2\)

\(\Leftrightarrow-2cosx-\sqrt{3}.cos2x=-1+\left(sinx+cosx\right)^2\)

\(\Leftrightarrow-2cosx=2sinx.cosx+\sqrt{3}cos2x\)

\(\Leftrightarrow-2cosx=sin2x+\sqrt{3}cos2x\)

\(\Leftrightarrow cos\left(\pi-x\right)=\dfrac{1}{2}.sin2x+\dfrac{\sqrt{3}}{2}.cos2x\)

\(\Leftrightarrow cos\left(\pi-x\right)=sin\left(2x+\dfrac{\pi}{3}\right)\)

\(\Leftrightarrow cos\left(\pi-x\right)=cos\left(\dfrac{\pi}{6}-2x\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}\pi-x=\dfrac{\pi}{6}-2x+k2\pi\\\pi-x=-\dfrac{\pi}{6}+2x+k2\pi\end{matrix}\right.\) ( k nguyên )

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5\pi}{6}+k2\pi\\x=\dfrac{7\pi}{18}-\dfrac{k2\pi}{3}\end{matrix}\right.\) ( k nguyên )

Vậy...

\(\dfrac{1+cosx+cos2x+cos3x}{2cos^2x+cosx-1}=\dfrac{1+cosx+2cos^2x-1+4cos^3x-3cosx}{2cos^2x+cosx-1}\)

\(=\dfrac{4cos^3x+2cos^2x-2cosx}{2cos^2x+cosx-1}=\dfrac{2cosx\left(2cos^2x+cosx-1\right)}{2cos^2x+cosx-1}=2cosx\)

3.

\(\dfrac{1}{2}-\dfrac{1}{2}cos2x-3cos2x-2=0\)

\(\Leftrightarrow-7cos2x-3=0\)

\(\Rightarrow cos2x=-\dfrac{3}{7}\)

\(\Rightarrow2x=\pm arccos\left(-\dfrac{3}{7}\right)+k2\pi\)

\(\Rightarrow x=\pm\dfrac{1}{2}arccos\left(-\dfrac{3}{7}\right)+k\pi\)

4.

ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)

\(tanx+2tanx=0\)

\(\Rightarrow3tanx=0\)

\(\Rightarrow tanx=0\)

\(\Rightarrow x=k\pi\) (loại do ĐKXĐ)

Vậy pt đã cho vô nghiệm

1.

\(\Leftrightarrow1-sin^2x+sinx=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1+\sqrt{5}}{2}>1\left(loại\right)\\sinx=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\\x=\pi-arcsin\left(\dfrac{1-\sqrt{5}}{2}\right)+k2\pi\end{matrix}\right.\) (\(k\in Z\))

2.

\(2cos^2x-\left(2cos^2x-1\right)+cosx=0\)

\(\Leftrightarrow cosx+1=0\)

\(\Leftrightarrow cosx=-1\)

\(\Leftrightarrow x=\pi+k2\pi\) (\(k\in Z\))

a/

\(cos^6x+sin^2x=1\)

\(\Leftrightarrow cos^6x-\left(1-sin^2x\right)=0\)

\(\Leftrightarrow cos^6x-cos^2x=0\)

\(\Leftrightarrow cos^2x\left(cos^4x-1\right)=0\)

\(\Leftrightarrow cos^2x\left(cos^2x-1\right)\left(cos^2x+1\right)=0\)

\(\Leftrightarrow-cos^2x.sin^2x=0\)

\(\Leftrightarrow sin^22x=0\)

\(\Leftrightarrow sin2x=0\)

\(\Leftrightarrow x=\frac{k\pi}{2}\)

b/

\(cos^6x-sin^6x=\frac{13}{18}cos^22x\)

\(\Leftrightarrow\left(cos^2x-sin^2x\right)\left(cos^4x+sin^4x+sin^2x.cos^2x\right)=\frac{13}{18}cos^22x\)

\(\Leftrightarrow cos2x\left[\left(sin^2x+cos^2x\right)^2-sin^2x.cos^2x\right]=\frac{13}{18}cos^22x\)

\(\Leftrightarrow cos2x\left(1-\frac{1}{4}sin^22x\right)=\frac{13}{18}cos^22x\)

\(\Leftrightarrow cos2x\left(1-\frac{1}{4}\left(1-cos^22x\right)\right)=\frac{13}{18}cos^22x\)

\(\Leftrightarrow cos2x\left(\frac{3}{4}+\frac{1}{4}cos^22x\right)=\frac{13}{18}cos^22x\)

\(\Leftrightarrow cos2x\left(\frac{1}{4}cos^22x-\frac{13}{18}cos2x+\frac{3}{4}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos2x=0\\\frac{1}{4}cos^22x-\frac{13}{18}cos2x+\frac{3}{4}=0\left(vn\right)\end{matrix}\right.\)

\(\Leftrightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\)

c/

\(cos^4x+sin^6x=cos2x\)

\(\Leftrightarrow\left(\frac{1+cos2x}{2}\right)^2+\left(\frac{1-cos2x}{2}\right)^3=cos2x\)

\(\Leftrightarrow cos^32x-5cos^2x+7cos2x-3=0\)

\(\Leftrightarrow\left(cos2x-1\right)^2\left(cos2x-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}cos2x=1\\cos2x=3\left(l\right)\end{matrix}\right.\)

\(\Leftrightarrow2x=k2\pi\)

\(\Rightarrow x=k\pi\)

Đặt t = cos2x

pt (*) <=> 2t^2 - 2[(căn3) + 1] + căn 3 = 0

<=> t = (3 + căn 3)/2 (loại) or t = (-1 + căn 3)/2 (nhận)

_Với t = (-1 + căn 3)/2 => cos2x = (-1 + căn 3)/2

<=> arccos ((-1 + căn 3)/2) + k2π (k∈Z)

or -arccos ((-1 + căn 3)/2) + k2π (k∈Z)