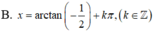2cos2x+cos2x=2
\(\Rightarrow\)2cos2x+2cos2x-1=2
\(\Rightarrow\)4cos2x=3
\(\Rightarrow\)cos2x=\(\dfrac{3}{4}\)
\(\Rightarrow\dfrac{1+cos2x}{2}=\dfrac{3}{4}\)
\(\Rightarrow4+4cos2x=6\)
\(\Rightarrow4cos2x=2\)
\(\Rightarrow cos2x=\dfrac{1}{2}\)
\(\Rightarrow cos2x=cos\dfrac{\Pi}{3}\)
\(\Rightarrow2x=\pm\dfrac{\Pi}{3}+k2\Pi\)
\(\Rightarrow x=\pm\dfrac{\Pi}{6}+k\Pi\)
\(PT\Leftrightarrow2\cos^2x-1+\cos2x=2-1=1\)\
\(\Leftrightarrow\cos2x+\cos2x=2\cos2x=1\)
\(\Leftrightarrow\cos2x=\dfrac{1}{2}\)
\(\Leftrightarrow2x=\pm\dfrac{\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+k\pi\left(k\in Z\right)\)
Vậy ....