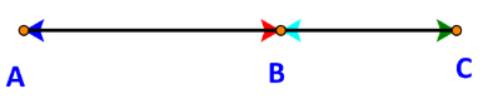
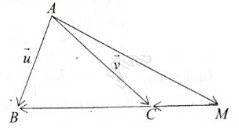
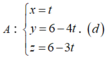Cho tam giác \(ABC\), trung tuyến \(AM\). Điểm \(E\) bất kì thỏa mãn \(2\overrightarrow{EA}+\overrightarrow{EC}=\overrightarrow{0}\). Đường thẳng \(d\) qua \(E\) song song với \(AB\) cắt \(AM,BC\) lần lượt tại \(D,F\). \(G\) nằm trên cạnh \(AB\) sao cho diện tích hai tam giác \(BFG,ADE\) bằng nhau. Biết \(\overrightarrow{AG}=k\overrightarrow{AB}\). Tìm giá trị \(k\).
A. \(k=\dfrac{1}{3}\)
B. \(k=\dfrac{1}{2}\)
C. \(k=\dfrac{1}{4}\)
D. \(k=\dfrac{2}{3}\)
(Giải chi tiết giúp em ạ, em cảm ơn)








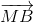 = 3
= 3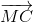 =>
=> 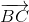 )
)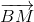 =
= 
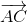 -
- 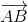 nên
nên 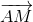 =
= 

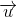 +
+