Tìm TXĐ của hàm số y=2cot(x+30°)

Những câu hỏi liên quan
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.1. TXĐ CỦA HÀM SỐCâu 1.Tìm tập xác định của hàm số ydfrac{sqrt{x-1}}{x-3}Câu 2.Tìm tập xác định của hàm số y sqrt[3]{x-1}Câu 3. Tìm tập xác định của hàm số ydfrac{sqrt[3]{1-x}+3}{sqrt{x+3}}Câu 4. Tìm tập xác định của hàm số ysqrt{left|x-2right|}
Đọc tiếp
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.
1. TXĐ CỦA HÀM SỐ
Câu 1.Tìm tập xác định của hàm số y=\(\dfrac{\sqrt{x-1}}{x-3}\)
Câu 2.Tìm tập xác định của hàm số y= \(\sqrt[3]{x-1}\)
Câu 3. Tìm tập xác định của hàm số y=\(\dfrac{\sqrt[3]{1-x}+3}{\sqrt{x+3}}\)
Câu 4. Tìm tập xác định của hàm số y=\(\sqrt{\left|x-2\right|}\)
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
Đúng 1
Bình luận (0)
Tìm chu kì của hàm số Y=2cot (x/3+π\4)
Hàm số \(y=2cot\left(\dfrac{x}{3}+\dfrac{\pi}{4}\right)\) tuần hoàn với chu kì \(T=\dfrac{\pi}{\left|\dfrac{1}{3}\right|}=3\pi\).
Đúng 0
Bình luận (1)
Tìm txđ của hàm số sau:\(y=\dfrac{x}{sinx+tanx}\)
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\sinx+tanx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\\dfrac{sinx\left(1+cosx\right)}{cosx}\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\end{matrix}\right.\)
\(\Leftrightarrow sin2x\ne0\)
\(\Rightarrow2x\ne k\pi\Rightarrow x\ne\dfrac{k\pi}{2}\)
Đúng 0
Bình luận (0)
tìm TXĐ D của hàm số y=3x-1/x-2
tìm TXĐ của hàm số y= \(\dfrac{x^2+x+1}{x^2-9}\)
1. Tìm TXĐ, TGT của hàm số: y=\(\sqrt{x+2}+\sqrt{2-x}\)
`@` H/s xác định `<=>{(x+2 >= 0),(2-x >= 0):}<=>{(x >= -2),(x <= 2):}<=>-2 <= x <= 2`
`=>TXĐ: D=[-2;2]`
`@-2 <= x <= 2`
`<=>{(0 <= x+2 <= 4),(2 >= -x >= -2):}`
`<=>{(0 <= x+2 <= 4),(4 >= 2-x >= 0):}`
`<=>{(0 <= \sqrt{x+2} <= 2),(2 >= \sqrt{2-x} >= 0):}`
`=>TGT` là `[0;2]`
Đúng 3
Bình luận (0)
\(y=\sqrt{x+2}+\sqrt{2-x}\)
y có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x+2>0\\2-x>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x>-2\\x>2\end{matrix}\right.\)
TXD D = \(\left(2;+\infty\right)\)
Đúng 0
Bình luận (1)
\(đk\left\{{}\begin{matrix}x+2\ge0\\2-x\ge0\end{matrix}\right.=>\left\{{}\begin{matrix}x\ge-2\\x\le2\end{matrix}\right.\)
\(=>TXĐ:\left[-2;2\right]\)
Đúng 2
Bình luận (1)
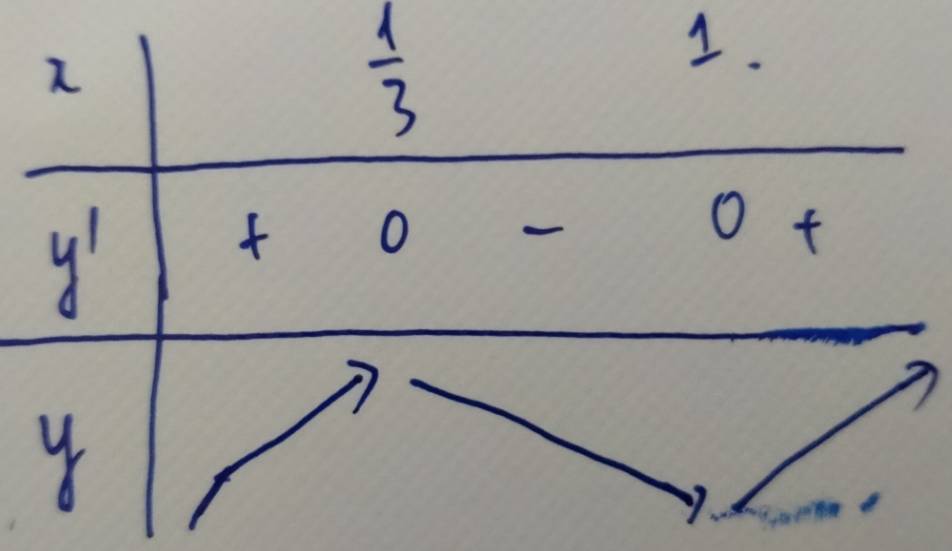
Tìm TXĐ và vẽ BBT của hàm số: y = x3 - 2x2 + x - 1
TXĐ: \(D=R\)
\(y=x^3-2x^2+x-1\\ \Rightarrow y'=3x^2-4x+1\)
\(y'=0\Leftrightarrow3x^2-4x+1=0 \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=1\end{matrix}\right.\)
Bảng biến thiên:
Đúng 0
Bình luận (0)
Tìm txđ của các hàm số sau
1. y = tan ( x - 2π/3)
2. y = cot ( x + π/6)
3. y = sin căn 1+x/ 2-x
ĐKXĐ:
a. \(cos\left(x-\dfrac{2\pi}{3}\right)\ne0\Rightarrow x-\dfrac{2\pi}{3}\ne\dfrac{\pi}{2}+k\pi\Rightarrow x\ne\dfrac{\pi}{6}+k\pi\)
b. \(sin\left(x+\dfrac{\pi}{6}\right)\ne0\Rightarrow x+\dfrac{\pi}{6}\ne k\pi\Rightarrow x\ne-\dfrac{\pi}{6}+k\pi\)
c. \(\dfrac{1+x}{2-x}\ge0\Rightarrow-1\le x< 2\)
Đúng 1
Bình luận (0)
Tìm tập xác định của hàm số sau
a) y=cot(\(3x+\dfrac{\pi}{6}\)) + \(\dfrac{tan2x}{sinx+1}\)
b) y=\(\sqrt{5+2cot^2x-sinx}\) + cot\(\left(\dfrac{\pi}{2}+x\right)\)
a.
\(\left\{{}\begin{matrix}sin\left(3x+\dfrac{\pi}{6}\right)\ne0\\cos2x\ne0\\sinx\ne-1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne-\dfrac{\pi}{18}+\dfrac{k\pi}{3}\\x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\\x\ne-\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
b.
Do \(5+2cot^2x-sinx=4+2cot^2x+\left(1-sinx\right)>0\) nên hàm xác định khi:
\(\left\{{}\begin{matrix}sinx\ne0\\sin\left(x+\dfrac{\pi}{2}\right)\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}sinx\ne0\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow sin2x\ne0\)
\(\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
Đúng 2
Bình luận (0)





















