Các câu hỏi tương tự
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.1. TXĐ CỦA HÀM SỐCâu 1.Tìm tập xác định của hàm số ydfrac{sqrt{x-1}}{x-3}Câu 2.Tìm tập xác định của hàm số y sqrt[3]{x-1}Câu 3. Tìm tập xác định của hàm số ydfrac{sqrt[3]{1-x}+3}{sqrt{x+3}}Câu 4. Tìm tập xác định của hàm số ysqrt{left|x-2right|}
Đọc tiếp
I. HÀM SỐ, TXĐ, CHẴN LẺ, ĐƠN ĐIỆU, ĐỒ THỊ.
1. TXĐ CỦA HÀM SỐ
Câu 1.Tìm tập xác định của hàm số y=\(\dfrac{\sqrt{x-1}}{x-3}\)
Câu 2.Tìm tập xác định của hàm số y= \(\sqrt[3]{x-1}\)
Câu 3. Tìm tập xác định của hàm số y=\(\dfrac{\sqrt[3]{1-x}+3}{\sqrt{x+3}}\)
Câu 4. Tìm tập xác định của hàm số y=\(\sqrt{\left|x-2\right|}\)
tìm TXĐ của hàm số y= \(\dfrac{x^2+x+1}{x^2-9}\)
tìm TXĐ của hàm số:
y=\(\left\{{}\begin{matrix}\dfrac{2x-3}{x-1},x\le0\\-x^2+3x,x>0\end{matrix}\right.\)
tìm TXĐ của hàm số:
a) y=\(\dfrac{\sqrt{x^2-x+1}}{x-3}\)
b)y=\(\dfrac{\sqrt{5-2x}}{\left(x-2\right)\sqrt{x-1}}\)
cho hàm số \(y=\sqrt{4x+m-3}\)
tìm m để txđ của hàm số là \(\left[2,+\infty\right]\)
Tìm TXĐ của hàm số sau
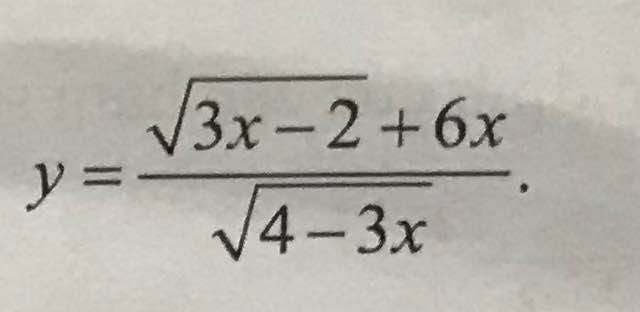
Tìm tập xác định D của hàm số
y
3
x
−
2
+
6
x
4
−
3
x
A.
D
2
3
;
4
3...
Đọc tiếp
Tìm tập xác định D của hàm số y = 3 x − 2 + 6 x 4 − 3 x
A. D = 2 3 ; 4 3
B. D = 3 2 ; 4 3
C. D = 2 3 ; 3 4
D. D = − ∞ ; 4 3
1) Cho hàm số: yx^2-3x+4 có đồ thị là P và đường thẳng d có phương trình:y2x-m, và m là tham số. Tìm các giá trị của m để d cắt P tại hai điểm phân biệt A,B sao cho: OA^2+OB^257 và khi đó O là toa độ góc2) Cho hàm số fleft(xright)sqrt{3-x}-sqrt{3+x}-x^3-x. Tìm tất cả giá trị của tham số a để tập nghiệm của bất phương trình fleft(2x-1right)fleft(-2aright) có ít nhất là 3 số nguyên
Đọc tiếp
1) Cho hàm số: \(y=x^2-3x+4\) có đồ thị là P và đường thẳng d có phương trình:
\(y=2x-m\), và m là tham số. Tìm các giá trị của m để d cắt P tại hai điểm phân biệt \(A,B\) sao cho: \(OA^2+OB^2=57\) và khi đó O là toa độ góc
2) Cho hàm số \(f\left(x\right)=\sqrt{3-x}-\sqrt{3+x}-x^3-x\). Tìm tất cả giá trị của tham số a để tập nghiệm của bất phương trình \(f\left(2x-1\right)>f\left(-2a\right)\) có ít nhất là 3 số nguyên
Tìm tập xác định D của hàm số
y
3
x
−
1
2
x
−
2
A. D R B. D
(
1
;
+
∞
)
C. D R∖{1} D. D
[
1
;
+
∞
)
Đọc tiếp
Tìm tập xác định D của hàm số y = 3 x − 1 2 x − 2
A. D = R
B. D = ( 1 ; + ∞ )
C. D = R∖{1}
D. D = [ 1 ; + ∞ )











